1.2.4. Последовательность независимых испытаний (схема Бернулли)
При постоянных условиях S выполняется n независимых испытаний. Результатом каждого испытания может быть только одно из двух противоположных событий: A или . Введем обозначения для вероятностей этих событий: P(A) = p, P( ) = q = 1 - p.
Требуется
найти вероятность
того, что при указанных условиях событие
A
произойдет ровно m
раз. Комбинаций,
в которых событие A
произойдет ровно m
раз, может
быть несколько.
Реализация каждой такой комбинации
– сложное
событие, которое представляет собой
последовательность
событий A
и
.
Обозначим эти сложные события буквой B, индекс у которой будет соответствовать номеру одной из возможных последовательностей:
=
. . . . . . . . . . . . . . . .
=
. . . . . . . . . . . . . . . .
=
.
Общее количество таких последовательностей равно числу сочетаний из n по m, поскольку порядок следования их элементов неразличим, то есть
.
События
попарно несовместны, поэтому в соответствии
с аксиомой о счетной аддитивности
,
но
независимо от i
, поэтому вероятность того, что при n
независимых испытаниях событие A
появится ровно m
раз, равна
.
1.3. Дискретные случайные величины
Случайная величина – функция случайного события, = f(). Область определения функции – пространство элементарных исходов , область значений – все вещественные числа.
Дискретная случайная величина – случайная величина, которая может принимать только счетное множество значений.
1.3.1. Распределение вероятностей дискретных случайных величин
Пусть
,
,
...,
–
полная группа непересекающихся событий
,
которые могут возникать при выполнении
некоторых испытаний в условиях S.
P
,
,
...,
– вероятности событий
.
Пусть
также каждому из событий
по какому-либо правилу поставлено во
взаимно однозначное соответствие
вещественное число
.
Так мы определили вещественную функцию
случайных событий.
При
выполнении испытаний эта функция будет
принимать значения
, 
,
. . . ,
с вероятностями 
.
Таким образом определена дискретная случайная величина набором значений, которые она может принимать, и набором вероятностей, с которыми она может принимать эти значения:
.
Векторная
запись этого определения экономнее:
,
где
– вектор значений
,
,
...,
,
– вектор вероятностей
.
С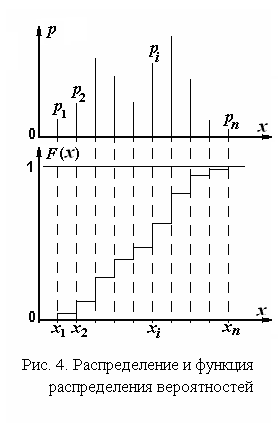
овокупность
значений
представляет собой наиболее полное
описание дискретной случайной величины
и называется распределением
вероятностей.
Поскольку
случайные события
образуют полную группу непересекающихся
событий, 
Наряду с распределением вероятностей в теории вероятностей используется еще одна полная характеристика случайных величин, а именно, функция распределения вероятностей:
F(x)
= P(
).
На рис. 4 приведен пример графического представления распределения вероятностей и функции распределения вероятностей дискретной случайной величины. Распределение вероятностей дискретной случайной величины изображается решетчатой функцией, высота каждого вертикального отрезка пропорциональна вероятности, с которой случайная величина принимает соответствующее значение.
Как следует из математического определения, функция распределения является неубывающей ступенчатой функцией. Каждый скачок этой функции происходит при значениях, которые может принимать случайная величина, а высота этих скачков пропорциональна соответствующим вероятностям.
Примером дискретной случайной величины может служить величина, порожденная бросанием шестигранной игральной кости. Случайным событием является положение кости на плоскости, которое она принимает в результате ее бросания на эту плоскость. Число вариантов этих положений – шесть, и если кость выполнена в виде идеального куба, то эти положения равновероятны. Правило, в соответствии с которым каждому такому случайному событию сопоставлено число, реализовано путем нанесения на грани кости целых чисел от одного до шести. Таким образом определена случайная величина
.
Поскольку все вероятности одинаковы, распределение вероятностей подобного вида называется равномерным распределением, а соответствующая случайная величина – равномерно распределенной случайной величиной.
Графическое представление такого распределения – решетчатая функция с отрезками равной высоты. Высота ступенек функции распределения одинакова.