2.5.5. Проверка гипотезы о виде плотности распределения

2.5.5.1. Критерий “хи-квадрат”

Из генеральной совокупности X, образованной случайной величиной , извлечена выборка . Выдвигается предположение о том, что плотность распределения случайной величины есть , где – вектор параметров. Для проверки этого предположения по выборочным данным вычисляются оценки параметров и проверяется сложная гипотеза:

: плотность распределения случайной величины  есть

против альтернативы

: плотность распределения случайной величины  не .

Поскольку эта гипотеза сложная, задается только вероятность ошибки первого рода , которая в подобных случаях именуется уровнем значимости.

Степень различия между гистограммой и предполагаемой плотностью распределения выражается суммой квадратов разностей

,

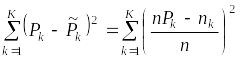где

,

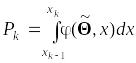то есть вероятность попадания значения случайной величины в интервал при условии справедливости нулевой гипотезы, - оценки этих вероятностей, где – количество выборочных значений, попавших в интервал , n – объем выборки, К – общее количество интервалов, на которых построена гистограмма.

К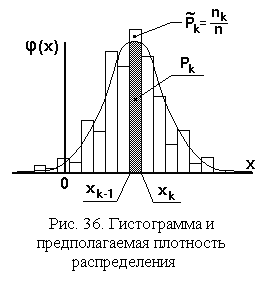 аждое слагаемое этой суммы является случайной величиной, поскольку случайным является число . Если выборочные значения независимы, – событие, которое заключается в том, что выборочное значение попадает в интервал , – противоположное событие. Поэтому в соответствии со схемой Бернулли вероятность того, что при n экспериментах событие произойдет ровно раз, равна (см. разд. 1.3.2) .

Из результатов, полученных в примере разд. 1.3.5, следует, что

, .

Пользуясь формулами для моментов линейных функций от случайных величин, приведенными в разд. 1.3.4, можем записать, что

, .

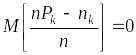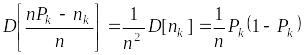Преобразуем исходную сумму путем деления каждого из слагаемых на его дисперсию. Получим сумму

.

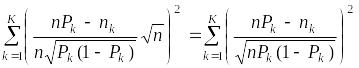Видно, что после этого деления

, .

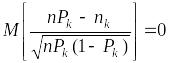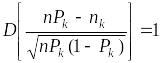Строго говоря, случайная величина

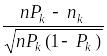
является дискретной из-за того, что порождена дискретной случайной величиной , распределенной по биномиальному закону. При дискретности значений величины , равной 1, дискретность значений вновь сформированной случайной величины равна , и с ростом n убывает до нуля. Поэтому можно говорить, что эта случайная величина в ассимптотике при n   становится непрерывной.

С другой стороны, по теореме Муавра-Лапласа (см. разд. 1.3.7), распределение вероятностей случайной величины при n   аппроксимируется значениями

.

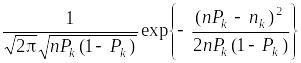После выполненных преобразований и с учетом того, что при n   дискретность значений случайной величины

уменьшается до нуля, мы имеем право говорить, что эта случайная величина распределена асимптотически нормально с параметрами (0, 1), то есть

.

Как известно из разд. 2.3.4.2, в), плотность распределения суммы квадратов таких случайных величин есть плотность распределения хи-квадрат. Таким образом, окончательно можем записать формулу для вычисления статистики критерия “хи-квадрат”, плотность распределения которой при условии справедливости нулевой гипотезы есть плотность распределения хи-квадрат с числом степеней свободы K - r, где K – количество слагаемых в сумме (то есть число интервалов, на которых построена гистограмма), r – число параметров предполагаемой плотности распределения, которые были определены по выборочным данным (то есть число связей, наложенных на выборочные данные):

.

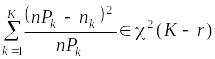Поскольку, как правило, сомножитель (1 - в знаменателях слагаемых опущен.

Подобный функционал был использован нами ранее в разд. 2.3.6 для нахождения оценок параметров плотности распределения методом минимума .

При заданной вероятности ошибки первого рода , здесь – уровня значимости, критическое значение (нижняя граница критической области ) назначается из следующих соображений.

При справедливости нулевой гипотезы маловероятно, чтобы статистика критерия оказалась слишком большой. Ограничимся таким критическим значением, вероятность превышения которого будет не более заданного значения . Поскольку нам известно, что при условии справедливости нулевой гипотезы статистика критерия распределена приблизительно по закону , мы можем принять в качестве критического значения – процентную квантиль .

Таким образом, сформирован критерий “хи-квадрат” проверки гипотезы о виде плотности распределения (или закона распределения) генеральной совокупности по экспериментальным данным.

П р о ц е д у р а п р о в е р к и г и п о т е з ы о виде плотности распределения по критерию “хи-квадрат”.

1. Задают уровень значимости 

2. По выборочным данным строят гистограмму в соответствии с указаниями разд. 2.2.

3. Вычисляются точечные оценки моментов.

4. Из теоретических соображений, по виду гистограммы, по соотношениям между моментами, по значениям асимметрии и эксцесса выдвигается гипотеза о виде плотности распределения .

5. Вычисляются оценки r параметров предполагаемой плотности распределения, в результате будет получена плотность распределения .

6. С использованием вычисляются вероятности

.

7. Вычисляется статистика критерия

.

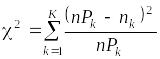8. Полученное значение сравнивается с критическим значением

,

где r – количество оцениваемых параметров предполагаемой плотности распределения .

9. Если делается вывод о том, что экспериментальные данные не подтверждают справедливость выдвинутой гипотезы или о том, что отсутствуют достаточные основания для того, чтобы считать нулевую гипотезу справедливой. Гипотеза пересматривается, выдвигается новая нулевая гипотеза, переход на п. 4 настоящей процедуры.

10. Если делается вывод о том, что экспериментальные данные подтверждают справедливость выдвинутой гипотезы или о том, что имеются достаточные основания для того, чтобы считать нулевую гипотезу справедливой.

Сделаем замечание о том, что с уменьшением вероятности  возрастает критическое значение , а это значит, что объективно растет вероятность ошибочного подтверждения нулевой гипотезы, когда она неверна. Крайний случай иллюстрирует это положение: если задать  = 0, то критическое значение , а это означает, что нулевая гипотеза, какой бы она ни была, не будет подвергаться сомнению ни при каком значении статистики критерия.