2.5.3. Простые гипотезы

Простой называется гипотеза о значении числовой характеристики или параметра, когда область значений, предполагаемых этой гипотезой, и область альтернативных значений - каждая из них являются одноточечной.

В других случаях гипотеза называется сложной.

Пример простой гипотезы.

Плотность распределения генеральной совокупности – нормальна, дисперсия известна и равна . Из генеральной совокупности X извлечена выборка . Проверяется простая гипотеза

: против альтернативы : .

Примеры необходимости проверки подобного рода гипотез в технике:

при цифровой передаче данных в условиях действия сильных помех с целью различения передаваемых двоичных символов 0 и 1;

в системах управления технологическими процессами с целью выявления состояния двухпозиционных устройств, контроля исполнения дискретных управляющих воздействий, обнаружения разладки технологического процесса и т.д.

Д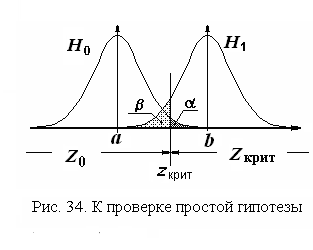 ля проверки этой гипотезы подходящей статистикой является среднее арифметическое значение, плотность распределения которого, как мы уже выяснили, также нормальна с дисперсией , а математическое ожидание равно a или b – в зависимости от того, какая из двух гипотез реально имеет место.

В случае справедливости гипотезы , в случае справедливости гипотезы . Эти две плотности распределения статистики приведены на рис. 34. Они пересекаются, и стоит задача определения границы областей и , то есть критического значения , чтобы обеспечить требуемые значения вероятностей ошибочных решений  и . Эти вероятности показаны на рис.34, как площади под кривыми плотностей распределения статистики, соответствующих гипотезам и .

В самом деле, если гипотеза справедлива, среднее арифметическое значение из-за действия случайных факторов может попасть в критическую область с вероятностью . Тогда, если так случится, будет сделан ошибочный вывод, который приведет к отклонению этой, на самом деле справедливой гипотезы.

В противном случае, когда справедлива гипотеза , среднее арифметическое значение из-за действия случайных факторов может попасть в область с вероятностью , что также приведет к ошибочному выводу.

Видно (см. рис. 34), что перемещением границы между областями и можно устанавливать желательное соотношение между вероятностями  и . Но может оказаться, что их значения слишком велики, и перемещение критического значения не приводит к их снижению. В таком случае необходимо увеличивать объем выборки. В результате дисперсия среднего арифметического уменьшится, его плотность распределения сузится, общая площадь под обеими кривыми уменьшится и, следовательно, уменьшатся вероятности ошибочных решений.

Этот пример показывает, что при проверке простой гипотезы контролируются значения обеих вероятностей ошибочных решений:  и .

2.5.4. Сложные гипотезы

Пример сложной гипотезы. Плотность распределения генеральной совокупности нормальная, дисперсия известна и равна . Из генеральной совокупности X извлечена выборка . Проверяется сложная гипотеза

: против альтернативы : .

Примеры необходимости проверки подобного рода гипотез:

выявление разладки технологического процесса по параметру a;

распознавание перехода значения регулируемого параметра через уставку;

выявление превышения некоторой характеристикой установленной нормы (при медицинской диагностике, экологическом мониторинге, контроле качества пищевых продуктов, при сертификационных и иных испытаниях изделий и т.д.).

Поскольку проверяются гипотезы о математическом ожидании, как и в предыдущем разделе, подходящей статистикой для проверки этой гипотезы является среднее арифметическое, плотность распределения которого нормальна с дисперсией .

На рис. 35 приведены примеры двух вариантов расположения плотностей распределения средних арифметических значений, соответствующих гипотезам и : при значительном удалении друг от друга истинных значений математических ожиданий (см. рис. 35, а) и при близком их расположении.

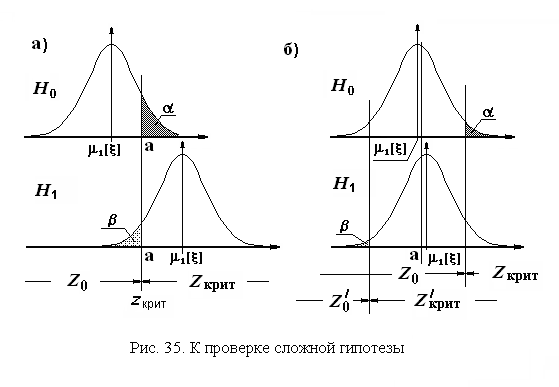
Если в первом варианте в качестве критического значения выбрать значение а, и сравнивать с ним получающееся среднее арифметическое значение, то возможно достижение достаточно малых значений вероятностей ошибочных решений  и . Однако, формулировка сложной гипотезы допускает вариант, показанный на рис. 35, б. В этой ситуации, если критическим значением является а, вероятности  и  сколь угодно близки к 0,5, что для практики недопустимо. Можно уменьшить вероятность ошибки первого рода  путем перемещения границы между областями и вправо. Но тогда вероятность ошибки второго рода будет недопустимо близка к единице, поскольку в этом случае она равна площади под кривой плотности распределения статистики , соответствующей гипотезе , по всей области , то есть области, при попадании в которую принимается решение о непротиворечивости экспериментальным данным гипотезы .

Попытка уменьшить значение вероятности  путем перемещения влево критического значения, то есть границы между областями и (на рис. 35 эти области обозначены, как и ), приводит к недопустимо близкому к единице значению вероятности ошибки первого рода .

Из этого следует, что при проверке сложных гипотез может контролироваться только одна из вероятностей ошибочного решения: либо , либо . Значение другой из них не гарантируется и может быть сколь угодно близким к единице.

Это обстоятельство является существенным недостатком описанного метода проверки сложных гипотез.