Минимально необходимый объем выборки

для нахождения непараметрических толерантных пределов при Р = 0.95

Q	0.8	0.9	0.95	0.99	k
n	32	45	59	90	0
n	59	77	93	130	1
n	84	105	124	165	2
n	109	132	153	197	3

За независимость от вида плотности распределения исследуемой генеральной совокупности приходится “платить” существенным увеличением объема выборки (см. табл. 4). Кроме того, становится ясно, почему в качестве толерантных пределов выбираются члены вариационного ряда, расположенные поближе к его краям.

Ранее подробно был рассмотрен случай нахождения непараметрических толерантных пределов для интервального оценивания интерквантильного промежутка , симметричного относительно математического ожидания (см. разд. 1.6.2, рис. 10, а).

В ряде случаев, когда математическое ожидание случайной величины невелико по сравнению с ее среднеквадратическим значением, объем выборки может быть уменьшен без ущерба для достоверности оценок. Как правило, такая ситуация встречается при экспериментальном определении характеристик погрешности средств измерений или результатов измерений, или характеристик точности регуляторов, позиционеров, систем автоматического управления и регулирования, когда в составе погрешности этих устройств имеются и случайные, и систематические составляющие, но в документации на эти средства установлены нормы на сумму этих составляющих. Пример такого интерквантильного промежутка приведен в разд. 1.6.2 (см. на рис. 10, б). Он обозначен там и имеет границы [–g, g]. В подобных случаях рекомендуется поступать следующим образом.

Исходная выборка значений погрешностей , среди которых имеются положительные и отрицательные значения, преобразуется в выборку, состоящую из абсолютных величин этих исходных значений. В результате весь вариационный ряд оказывается на правой полуоси, что снимает заботу об отбрасывании первого статистически эквивалентного блока, а именно, , поскольку обе границы доверительного интервала для интерквантильного промежутка, симметричного относительно начала координат, определяются конечными членами вариационного ряда, составленного из модулей выборочных значений .

В этом случае толерантные пределы , составленные на основе одного лишь максимального члена этого вариационного ряда, являются границами доверительного интервала для интерквантильного промежутка (см. разд. 1.6.2, рис.10, б), если, конечно, объем выборки достаточен для этого. Поскольку в этом конкретном случае не отбрасывается ни один статистически эквивалентный блок (ибо первый, как уже было сказано, нас не интересует, а последним блоком является ), минимально необходимый объем выборки находят при k = 0 из неравенства

.

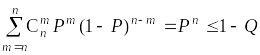Этому варианту соответствует первая строчка в табл. 4.

Понятно, что при желании застраховаться от вредного влияния грубых промахов или помех количество отбрасываемых членов может быть увеличено в два раза при том же объеме выборки. При этом доверительная вероятность не изменится, а объем выборки, необходимый при отбрасывании одного, двух и более крайних членов, находится из последующих строк данной таблицы. Видно, что достигается существенная экономия объема выборки. “Платой” за это является расширение доверительного интервала.