Значения толерантного множителя и квантилей

нормальной плотности распределения для P = 0.95

n Q	5	8	12	20	100
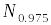
0.9	4.152	3.264	2.863	2.564	2.170	1.96
0.95	5.079	3.732	3.162	2.752	2.231	1.96

ширина которого пропорциональна s, с коэффициентом пропорциональности . С этой целью в табл. 3 приведено сравнение квантилей нормальной плотности распределения и толерантного множителя для одного значения вероятности P = 0.95.

Заметим, что, в отличие от доверительных интервалов для математического ожидания и дисперсии, границы доверительного интервала для интерквантильного промежутка, то есть толерантные пределы, с увеличением объема выборки приближаются к границам искомого интерквантильного промежутка. В пределе при n ширина этого доверительного интервала равна ширине искомого интерквантильного промежутка.

2.4.6.2. Непараметрические толерантные пределы

Непараметрические толерантные пределы являются границами доверительного интервала для интерквантильного промежутка. Для того, чтобы их определить, не требуется априорная информация о виде плотности распределения генеральной совокупности, а поэтому точечные оценки параметров не используются. В англоязычной литературе для обозначения подобного рода статистического оценивания характеристик случайных величин применяется термин “distribution-free estimation”.

В качестве непараметрических толерантных пределов служат непосредственно выборочные значения - члены вариационного ряда (см. [6], стр. 338).

Принцип нахождения непараметрических толерантных пределов, иными словами, границ доверительных интервалов для интерквантильного промежутка, не зависящих от вида плотности распределения, основывается на результате, полученном ранее в примере 2 разд. 1.6.7. Этот же результат использован при построении выборочной функции распределения в разд. 2.2 (см. рис. 26). Как следует из указанных материалов, вероятностные меры полуоткрытых интервалов, заключенных между двумя соседними членами вариационного ряда в среднем, по множеству групп однородных экспериментов объемом n одинаковы и равны 1/n.

Это происходит по следующей причине. Выборка извлекается из генеральной совокупности, образованной всеми значениями случайной величины ξ, интегральная функция распределения которой есть . Поскольку при любом распределении ξ случайная величина распределена равномерно в интервале (0, 1), значения функции от выборочных значений также распределены равномерно в том же интервале. При нанесении выборочных значений на числовую ось эти выборочные значения выстраиваются в вариационный ряд . Вероятностные меры интервалов :

.

Поскольку случайная величина распределена равномерно, эти вероятностные меры одинаковы на множестве всех возможных групп выборочных значений, извлеченных из генеральной совокупности, образованной случайной величиной ξ.

В связи с этим свойством полуоткрытые интервалы между соседними членами вариационного ряда и называются статистически эквивалентными блоками. Первый статистически эквивалентный блок . Последний статистически эквивалентный блок .

Вероятностная мера полуоткрытого интервала равна, по частотному определению вероятности, (n – 1)/n, поскольку один статистически эквивалентный блок, а именно, не входит в интервал . Такой же результат мы получим при графическом определении этой же вероятности по выборочной функции распределения (см. разд. 2.2, рис. 26).

Вероятностная мера полуоткрытого интервала по той же причине равна (n – 3)/n, поскольку в этот интервал не входят статистически эквивалентные блоки , , .

Теперь уместно вспомнить, что нашей целью является определение границ такого доверительного интервала, который накрывает интерквантильный промежуток с вероятностью, не меньшей Q. Понятно, что, как и в предыдущем разделе,

и ,

то есть нижний и верхний толерантные пределы должны охватывать истинный интерквантильный промежуток с вероятностью Q. Это обстоятельство эквивалентно тому, что в силу монотонности вероятностной меры (см.разд. 1.2.2) , то есть исходная задача трансформируется в следующую.

Необходимо найти такие значения и , что вероятностная мера интервала между ними не меньше, чем вероятностная мера P искомого интерквантильного промежутка.

Из предыдущего материала настоящего раздела мы уже можем заключить, что вероятностная мера полуоткрытых интервалов, заключенных между элементами вариационного ряда, может быть просто определена путем подсчета относительного количества статистически эквивалентных блоков, находящихся (или попавших) в эти полуоткрытые интервалы.

По условию задачи требуется определить и обеспечить не точечную оценку этой вероятностной меры, а такое гарантированное значение этой меры, о котором с вероятностью, не меньшей Q, можно говорить, что истинное значение вероятности не меньше, чем заданное при определении искомого интерквантильного интервала, то есть P.

Материал разд. 2.4.2 предоставляет нам возможность решения этой задачи, которая является обратной по отношению к построению доверительного интервала для вероятности. Основное отличие заключается в том, что в разд. 2.4.2 мы имели уже полученные выборочные значения и заданную доверительную вероятность. В данном случае нам задана нижняя граница вероятности в виде вероятности P, для которой определен искомый интерквантильный промежуток, и задача заключается в определении условий, при которых интервал между элементами вариационного ряда будет с вероятностью Q иметь вероятностную меру, не меньше, чем P.

Таким образом, неравенство для определения нижней границы доверительного интервала для вероятности, приведенное в разд. 2.4.2, а именно

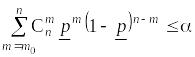
имеет теперь для нас несколько иной, скорее обратный, смысл.

Поскольку нижняя граница нам задана и равна P, верхняя граница вероятности равна 1 и здесь нас не интересует, поэтому примем Q = 1 – . Теперь, руководствуясь настоящим неравенством, нам остается подобрать такие значения n и , чтобы обеспечить заданные значения P и Q.

Примеры точечных оценок вероятностной меры интервалов, заключенных между элементами вариационного ряда, свидетельствуют о том, что, по сути дела, это не что иное, как оценка вероятности по частости, то есть по относительной частоте попадания (нахождения) статистически эквивалентных блоков внутри этих интервалов. На основании этого выясненного факта и, учитывая близость вероятностей P и Q к единице, перепишем последнее неравенство в виде

,

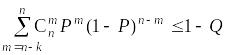где n - k – число статистически эквивалентных блоков, находящихся внутри интервала между такими элементами вариационного ряда, которые желательно объявить толерантными пределами или, иными словами, границами доверительного интервала, который покрывает искомый интерквантильный промежуток, определенный при вероятности P.

В теории непараметрического интервального оценивания число k именуется, как количество отброшенных статистически эквивалентных блоков. Понятно, что отбрасываемыми статистически эквивалентными блоками должны быть крайние блоки.

Это неравенство решают в двух вариантах постановки основной задачи:

1. Зафиксировано количество k статистически эквивалентных блоков, не попавших между теми элементами вариационного ряда, которые желательно принять в качестве толерантных пределов, и отыскивается минимальный объем выборки, необходимый для обеспечения заданных параметров P и Q.

2. Зафиксирован объем выборки, отыскивается количество k статистически эквивалентных блоков, которые необходимо отбросить, чтобы оставшиеся крайние члены вариационного ряда принять в качестве толерантных пределов, обеспечивающих заданные значения параметров P и Q.

В большинстве случаев задача ставится и решается в первом варианте, и мы вскоре увидим, почему.

Пусть при подготовке испытаний (измерений) в качестве непараметрических толерантных пределов планируется использовать крайние члены вариационного ряда. Это решение может быть принято при практическом отсутствии факторов, способных привести к резким выбросам отдельных результатов. На нашем языке это означает, что из всех статистически эквивалентных блоков отбрасывается один первый блок , и доверительным интервалом оказывается полуоткрытый интервал . Необходимый объем выборки n находят как наименьшее решение неравенства

.

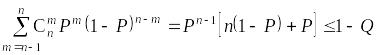При необходимости защиты от возможных импульсных помех или иных факторов, вызывающих резкие и значительные выбросы результатов измерений, пытаются принять в качестве толерантных пределов (доверительного интервала для интерквантильного промежутка) интервал , что означает отбрасывание трех статистически эквивалентных блоков. Необходимый объем выборки n находят как наименьшее решение неравенства

.

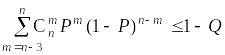Понятно, что в этом случае при фиксированных P и Q объем выборки должен возрасти.

В таблице 4 приведены результаты расчетов объема выборки, минимально необходимого для определения непараметрических толерантных пределов – границ доверительного интервала для интерквантильного промежутка при P = 0.95 и k = 1, 2, 3.

Таблица 4