2.3.5. Метод максимального правдоподобия
Точечные оценки, полученные методом максимального правдоподобия (ММП-оценки), являются эффективными оценками, хотя и могут быть смещенными. Для получения ММП-оценок необходима априорная информация о плотности распределения.
И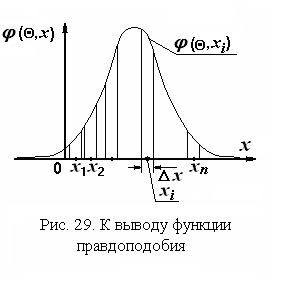
так,
пусть плотность распределения
генеральной
совокупности X
известна с точностью до параметров Θ,
подлежащих оцениванию. Из этой генеральной
совокупности извлечена выборка
.
Образуем
около каждого выборочного значения
непересекающиеся
интервалы
равной ширины, такие, чтобы каждое
выборочное значение находилось в
середине своего интервала (рис. 29).
Обозначим ширину этих интервалов x.
Расcчитаем
вероятность того, что каждое из выборочных
значений попадает в свой интервал:
.
В соответствии с принципом максимального правдоподобия в качестве оценок параметров Θ предлагается найти такие значения параметров, при которых имеющаяся выборка оказывается наиболее правдоподобной или, что то же самое, наиболее вероятной. Для этого необходимо найти максимум указанной выше вероятности. Предварительно сделаем два упрощения.
Первое – отбрасываем постоянные сомножители x, как не влияющие на положение максимума.
Второе – будем отыскивать максимум логарифма этой вероятности, ибо логарифмирование функции по основанию, большему единицы, не влияет на положение ее максимума, но в большинстве случаев приводит к значительному упрощению выкладок.
В результате этих действий получим логарифмическую функцию правдоподобия:
.
ММП-оценки параметров Θ находят путем поиска максимума функции правдоподобия
.
П
р и м е р 1. Случайная величина
распределена
нормально:
.
Требуется
найти ММП-оценку математического
ожидания случайной величины
по выборочным
значениям
.
Функция правдоподобия для поставленной задачи
.
Будем отыскивать максимум функции правдоподобия с помощью производной по а. Первое слагаемое не зависит от а, поэтому его учитывать не будем. Остается найти максимум отрицательного выражения, который достигается там, где достигается минимум его абсолютной величины. Поэтому ММП-оценка математического ожидания есть значение, при котором достигается максимум функции правдоподобия:
.
Продифференцируем минимизируемое выражение по а и приравняем производную нулю:
,
откуда сразу получаем ММП-оценку математического ожидания
.
Из этого факта с необходимостью следует эффективность среднего арифметического как оценки математического ожидания по выборке, извлеченной из нормальной генеральной совокупности. Об этом уже было упомянуто выше в разд. 2.3.4.1.
П
р и м е р 2. Измерения одной и той же
величины, значение которой равно a,
выполняются различными средствами
измерений, обладающими различными
случайными погрешностями, среднеквадратические
значения которых
.
Измерения, выполняемые каждым средством
измерений, однократные, погрешности
распределены нормально, систематические
составляющие погрешностей отсутствуют.
Требуется найти ММП-оценку значения измеряемой величины.
Подобная ситуация в математической статистике классифицируется как случай неравноточных измерений, в отличие от примера 1, который классифицируется как случай равноточных измерений.
В
этой ситуации каждое выборочное значение
извлекается из своей генеральной
совокупности, то есть
.
Функция правдоподобия теперь будет
иметь иной вид:
.
Дифференцируем функцию правдоподобия по a и приравниваем производную нулю:
,
откуда получаем ММП-оценку математического ожидания при неравноточных измерениях:
,
где
веса
обратно пропорциональны дисперсиям
случайных погрешностей измерений и в
сумме составляют единицу:
,
.
П р и м е р 3. Выборка извлечена из генеральной совокупности, распределенной по Лапласу. Плотность распределения
.
Необходимо найти ММП-оценки параметров a (математическое ожидание) и .
Функция правдоподобия имеет вид
.
Н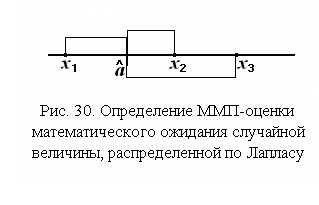
айдем
вначале ММП-оценку математического
ожидания а. Поскольку первое слагаемое
не содержит а, его значение не влияет
на положение максимума, поэтому мы его
исключим. Останется одно отрицательное
слагаемое, минимум модуля которого
совпадает по положению с максимумом
функции правдоподобия. Поэтому будем
отыскивать ММП-оценку
путем поиска минимума суммы
.
Эта сумма недифференцируема, и нам
придется находить искомую оценку с
привлечением геометрических построений.
Пусть
в результате эксперимента получено
всего три выборочных значения
,
которые разместились на вещественной
оси так, как показано на рис. 30.
Каждое
слагаемое минимизируемой суммы есть
расстояние от каждого выборочного
значения до математического ожидания.
В представленной ситуации (см. рис. 30),
на рисунке, одно из этих расстояний
входит в сумму дважды. Это расстояние
.
Видно, что рассматриваемая сумма
достигнет минимума только тогда, когда
оценка
совместится с
,
то есть с выборочной медианой. Добавляя
к этой небольшой выборке четное количество
элементов, мы придем к тому же выводу,
что ММП-оценкой математического ожидания
случайной величины, распределенной по
Лапласу, является выборочная медиана
.
А это означает, что эта оценка эффективна, о чем было упомянуто в разд. 2.3.4.1.
Теперь найдем ММП-оценку параметра .
.
Отсюда следует, что
.