1.2.2. Вероятность событий
Вероятность
(осуществления)
события – числовая характеристика
возможности события при условиях S.
Если
,
то вероятность события А
есть вероятностная мера множества
,
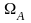обозначается P(A).
Приведем математические определения вероятности события.
К л а с с и ч е с к о е о п р е д е л е н и е:
P(A) есть отношение количества случаев, благоприятствующих появлению события A, к общему числу испытаний.
Ч а с т о т н о е о п р е д е л е н и е:
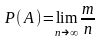
где n – общее число выполненных испытаний, m – количество случаев появления события A при этих испытаниях.
С о в р е м е н н а я а к с и о м а т и к а (А. Н. Колмогоров):
P(A) – неотрицательная монотонная счетно-аддитивная мера возможности случайного события, такая, что P(T) = 1.
Пояснения к этой аксиоматике:
неотрицательность: P(A) 0;
монотонность: если A B то P(A) P(B), то есть, если при наступлении события A обязательно наступает событие B, но обратное необязательно, то P(A) P(B);
счетная
аддитивность:
если условия S
определены, события
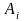попарно несовместны, то есть
,
,
то
.
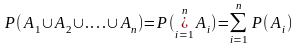В современной теории вероятностная мера определяется на классах событий. Классы событий образуются таким образом, чтобы они давали возможность определить вероятностную меру вначале на простейших событиях, а затем распространить ее на события любой сложности. Для этого класс событий должен содержать в себе не только сходящиеся в этом классе последовательности событий, но также их пределы. Обозначим класс событий .
Если
в условиях S
события
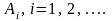принадлежат классу событий ,
и счетное объединение и счетное
пересечение этих событий также принадлежит
этому классу, то есть
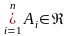и
,
то этот класс событий называется алгеброй событий.
Если
в этих же условиях
,
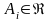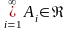и
,
то такой класс событий называется
сигма-алгеброй
(-алгеброй).
П р и м е р и з п л а н и м е т р и и. Класс всех многоугольников образует алгебру многоугольников, поскольку пересечение счетного количества многоугольников есть также многоугольник. Дополнение этого класса бесконечными пересечениями и объединениями многоугольников, что мы делали для определения меры (площади) круга, привело к образованию сигма-алгебры, и это позволило с помощью предельного перехода распространить меру (площадь) на геометрические фигуры, которые не являются многоугольниками, но суть пределы, к которым стремятся бесконечные сходящиеся последовательности многоугольников при их объединении и пересечении.
В итоге в соответствии с современной аксиоматикой теории вероятностей говорят, что случайные события и вероятностная мера этих событий определены тройкой: (, , P), где фигурируют введенные обозначения пространства элементарных событий, сигма-алгебры событий и вероятностной меры на них [4].
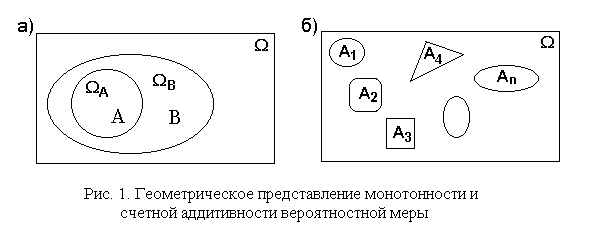
Для иллюстрации введенных понятий и свойств вероятностной меры, как было указано ранее, прибегают к геометрическому представлению событий в виде замкнутых фигур внутри прямоугольника, который представляет собой пространство элементарных событий . Вероятностная мера событий отождествляется с площадью соответствующих фигур с учетом того, что вероятностная мера всего прямоугольника равна единице.
Это представление событий и вероятностей показано на рис. 1, который иллюстрирует свойства монотонности (рис. 1, а) и счетной аддитивности (рис. 1, б) вероятностной меры.
Из аксиоматики Колмогорова следует:
а)
;
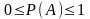б)
,
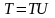откуда
следует: P(T)=1=P(T)+P()=1+P(),
и, наконец, P()=0;
в) A, B , A и B противоположны, то есть A B = , A B = Т;
тогда
P(A
B)
= P(A)+P(B)
= P(T)
= 1
, откуда
,
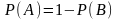то есть
,
;
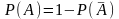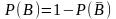г)
пусть A,
B
и
события
пересекаются, то есть
.
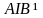В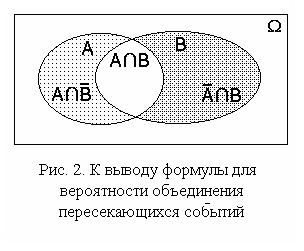
этом случае вероятность объединения
событий не равна сумме вероятностей.
Для вывода формулы представим объединение
пересекающихся событий A
и B
в виде объединения трех непересекающихся
событий (рис. 2):
.
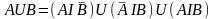Точно так же представим события
A
и B:
,
.
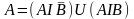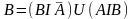К этим выражениям можно применить аксиому счетной аддитивности вероятностной меры:
,
, 
,
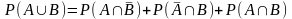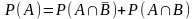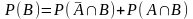откуда
следует, что
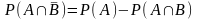и
.
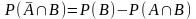Подставляя эти два выражения в первое, окончательно получим
=
=
.
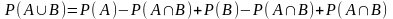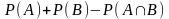Очевидно, что в случаях, когда события несовместны, то есть не пересекаются,
,
а
в общем случае всегда
.
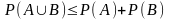