1.7.2.Числовые характеристики

Моменты случайных величин определяются, как и ранее, следующими формулами

начальные моменты k-го порядка

,

;

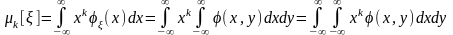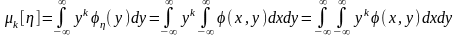центральные моменты k-го порядка:

, .

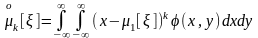Среди этих моментов самыми употребительными являются математи­ческие ожидания

и дисперсии

, .

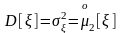Математическое ожидание случайного вектора есть вектор, компонентами которого являются математические ожидания соответствующих составляющих:

.

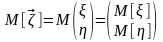Из условных моментов выделим лишь первые начальные (условные математические ожидания) и вторые центральные (условные дисперсии):

, ,

,

.

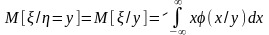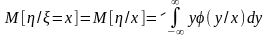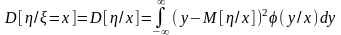Как и ранее, во всех случаях

, ,

, .

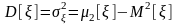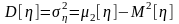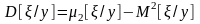Для двумерных случайных величин вводятся смешанные моменты:

начальные порядка k, r

;

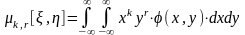центральные порядка k, r

.

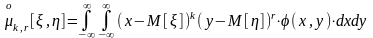Из них наиболее употребительным является центральный смешанный момент порядка (1, 1), который называется ковариацией и обозначается cov(, ):

.

Выясним связь между этим и начальным смешанным моментом того же порядка:

.

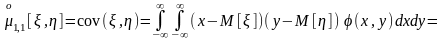
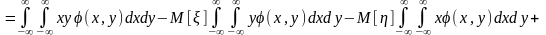
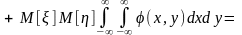
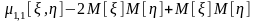В итоге получаем, что .

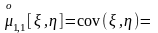
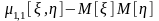Если случайные величины  и  независимы, в соответствии с признаком независимости, сформулированным ранее,

= ,

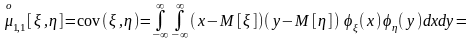
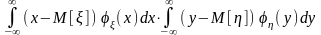то есть мы видим, что двукратный интеграл в этих условиях преобразуется в произведение однократных интегралов, каждый из которых равен 0. В самом деле,

.

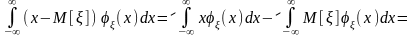
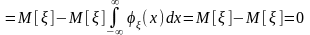Поэтому при условии независимости случайных величин  и  их первый центральный смешаный момент, или ковариация, равна 0.

При взаимно однозначной зависимости между  и , например, линейной 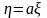, ковариация

.

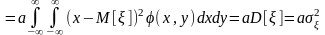Это означает, что ковариация есть характеристика степени зависи­мости между случайными величинами. Для того, чтобы избавиться от масштаба значений, принимаемых случайными величинами, в качестве показателя линейной зависимости используется частное от деления ковариации на произведение среднеквадратических значений случайных величин:

.

Эта величина называется коэффициентом корреляции. Случайные величины, у которых коэффициент корреляции равен нулю, называются некоррелированными. Независимые случайные величины с необходимостью некоррелированы. Обратное, вообще говоря, неверно! Из некоррелированности случайных величин их независимость, вообще говоря, не следует. Это понятно хотя бы потому, что из равенства нулю центрального смешанного момента порядка (1, 1) вовсе не следует, что все центральные смешанные моменты более высоких порядков также равны нулю.

Определим максимально возможное значение коэффициента корре­ляции. Естественно предположить, что своего максимального значения коэффициент корреляции достигает при взаимно однозначной связи между  и , например, линейной . Для этого случая нам известна ковариация между  и , а из разд. 1.6.5 следует, что , то есть . В результате получаем

,

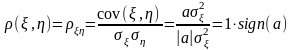а это означает, что

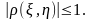
1.7.3. Ковариационная матрица случайного вектора

Компонентами ковариационной матрицы являются центральные моменты компонент случайного вектора: вторые центральные моменты и ковариации. Математическое определение ковариационной матрицы:

.

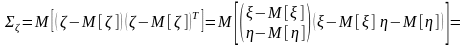
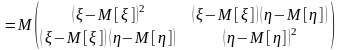Математическое ожидание случайной матрицы есть матрица, каждый элемент которой есть математическое ожидание соответствующего элемента исходной случайной матрицы. В итоге ковариационная матрица двумерного случайного вектора приобретает вид

.

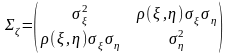Как видно, это симметричная квадратная матрица, ее размер соответствует размерности исходного случайного вектора. Определитель этой матрицы вычисляется достаточно просто:

.

Если случайные компоненты вектора независимы или хотя бы некоррелированы, ковариационная матрица становится диагональной, а ее определитель равен произведению диагональных элементов:

.

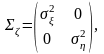
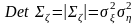При взаимно однозначной связи между  и , например линейной , коэффициент корреляции , а из этого следует, что определитель ковариационной матрицы равен нулю, то есть в этом случае матрица оказывается особенной. Этого следовало ожидать, поскольку если между составляющими случайного вектора существует взаимно однозначная связь, то, по сути дела, существует всего одна случайная величина, случайный вектор вырождается в скалярную (одноразмерную) случайную величину, и ковариационная матрица содержит только один элемент, то есть также вырождается в скаляр, а именно в значение дисперсии.

Для представления степени взаимной зависимости между компонентами случайного вектора применяется корреляционная матрица, элементами которой являются коэффициенты корреляции

.

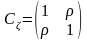Если компоненты случайного вектора независимы или хотя бы некоррелированы, корреляционная матрица становится единичной матрицей.