1.6.6.5. Плотность распределения Лапласа

График плотности распределения приведен на рис. 18. Плотность распределения симметрична относительно математического ожидания. Кривая плотности распределения описывается функцией

.

М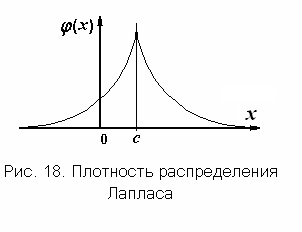 атематическое ожидание и медиана совпадают:

.

Для определения дисперсии воспользуемся характеристической функцией. Поскольку плотность распределения Лапласа симметрична и центральные моменты не зависят от смещения плотности распределения, примем с = 0. Тогда характеристическая функция получается из выражения

.

Если с  0, то в соответствии со свойством б) характеристических функций (см. разд. 1.6.4) появится экспоненциальный множитель

.

По свойству характеристических функций при с = 0

,

откуда следует, что дисперсия .

Четвертый центральный момент, асимметрия и эксцесс:

, As = 0, .

1.6.6.6. Плотность распределения Коши

График плотности распределения приведен на рис. 19. Плотность распределения симметрична относительно математического ожидания. Кривая плотности распределения описывается функцией

.

Плотность распределения симметрична, одномодальна.

Из общего выражения для моментов

в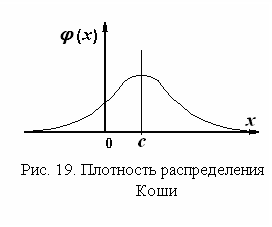 идно, что при всех целых значениях k > 0 этот несобственный интеграл не существует, поскольку порядок убывания подынтегральной функции на бесконечности при k > 0 не превышает 1. При k = 0 этот интеграл равен 1, что и должно следовать из условия нормировки плотности распределения.

В связи с этим математическое ожидание, дисперсия и моменты более высоких порядков случайной величины, распределенной по Коши, отсутствуют. Параметры плотности распределения Коши имеют названия: c – параметр сдвига (совпадает с модой и медианой),  – параметр масштаба.

Эксцесс случайной величины, распределенной по Коши, равен .

Характеристическая функция

.

Справедливость этого выражения обнаруживается при сопоставлении пары преобразований Фурье, связывающих плотность распределения Лапласа с ее характеристической функцией при c = 0. Здесь вид характеристической функции с точностью до множителя совпадает с видом плотности распределения Лапласа, а вид характеристической функции плотности Лапласа с точностью до того же множителя совпадает с видом плотности распределения Коши.

Заметим, что характеристическая функция случайной величины, распределенной по Коши, недифференцируема в нуле, и это еще один признак отсутствия моментов данной случайной величины.

1.6.6.7. Экспоненциальное семейство распределений

Представляемое здесь семейство плотностей распределений описывается функцией:

, где ,

p – параметр семейства, [] – гамма-функция (будет представлена в разделе 1.6.6.8). Все плотности распределения семейства симметричны, математическое ожидание совпадает с медианой и модой и равно c , эксцесс плотностей семейства равен

.

При p = 1 членом этого семейства является плотность распределения Лапласа, при p = 2 – нормальная плотность распределения.

В самом деле, при p = 1 и плотность распределения приобретает вид

,

а это и есть плотность распределения Лапласа, параметр которой в этом случае , ex = 6.

При p = 2 и плотность распределения принимает вид:

, ex = 3,

что и требовалось показать.

При дальнейшем увеличении параметра p плотность распределения приобретает форму, приближающуюся к форме равномерной плотности. При этом все плотности семейства симметричные с математическим ожиданием, равным c.