1.6.5. Линейные функции непрерывных случайных величин

Пусть задана функция случайной величины: 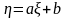. Вычислим математическое ожидание и дисперсию этой функции.

,

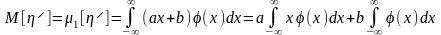откуда получаем:

,

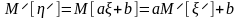иными словами, математическое ожидание линейной функции есть функция математического ожидания.

,

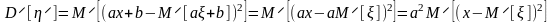откуда:

.

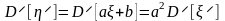Как и следовало ожидать, дисперсия не зависит от сдвига, а множитель выносится за знак дисперсии во второй степени.

1.6.6. Примеры плотности распределения непрерывных случайных величин

1.6.6.1. Случайная величина – интервал времени между импульсами

В простейшем потоке

Простейший случайный поток импульсов, заявок на обслуживание и тому подобных последовательностей случайных событий задается следующими свойствами:

поток импульсов (заявок) рассматривается в течение интервала времени, равного t;

в любом бесконечно малом, но не нулевом промежутке времени t, на которые поделен интервал времени (0, t] и который будем называть элементарным промежутком, с вероятностью p > 0 может появиться только один импульс (одна заявка);

появление импульса (заявки) в каждом из элементарных промежутков времени t есть событие, не зависящее от предыстории, то есть от появления импульса (заявки) в преды­дущие промежутки времени, это свойство –отсутствие последействия, или отсутствие памяти.

Такие условия осуществления событий, которые заключаются в случайном появлении импульсов (заявок) в следующие друг за другом элементарные промежутки времени, в точности соответствуют схеме Бернулли последовательности независимых испытаний (см. разд. 1.3.2). Если n – количество элементарных промежутков на интервале (0, t], то t = nt, а np – математическое ожидание количества импульсов (заявок) на этом интервале (то есть среднее значение их количества). Тогда естественным образом может быть вычислена средняя частота или интенсивность следования импульсов (заявок) в течение интервала (0, t] как отношение среднего их количества за этот интервал к длительности интервала: 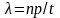. Отсюда, в частности, следует, что np = t. Единица измерения частоты  – [1/c] .

Найдем функцию распределения непрерывной случайной величины  – времени между двумя последовательными импульсами (заявками) в потоке:

.

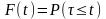Неравенство 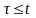выполняется, когда за время t появляется один импульс (заявка), или два импульса (заявки), или три импульса (заявки) и т. д. Определить вероятность бесконечного объединения подобных событий затруднительно. Гораздо легче и продуктивнее определить эту вероятность через вероятность противоположного события, а именно, через вероятность того, что за время t не появится ни одна заявка (отказ, импульс), то есть

.

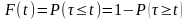Напомним, что исходной моделью для модели простейшего потока была схема независимых испытаний Бернулли (см. разд. 1.3.2). Поскольку потоки указанных событий реализуются в непрерывном времени, устремим t к нулю (при этом n 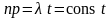  , ), и с использованием теоремы Пуассона (см. разд.1.3.6) найдем вероятность появления m импульсов в n интервалах времени, или, что то же самое, в течение времени t, как предел :

.

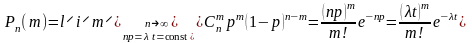Вероятность того, что в течение времени t не появится ни один импульс (или ни одна заявка), то есть m = 0, равна 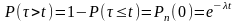. Отсюда функция распределения интервала времени между двумя последовательными импульсами (заявками) в случайном потоке

.

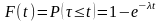П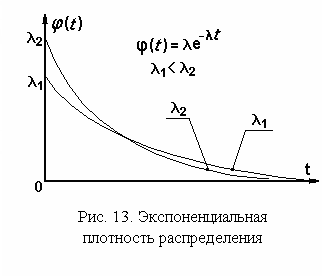 лотность распределения этой случайной величины есть производная от F(t) по t:

.

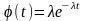В результате мы получили экспоненциальную плотность распределения или экспоненциальный закон распределения.

Вид кривой экспоненциальной плотности распределения при различных значениях параметра  представлен на рис. 13. Фигуры, ограниченные кривой плотности распределения и осью абсцисс, равновелики, их площади равны 1. Характеристическая функция экспоненциального распределения вычисляется, по определению (разд. 1.6.4), как интеграл:

.

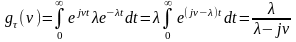Математическое ожидание и дисперсию случайного интервала времени между событиями (заявками, отказами, импульсами) находим, пользуясь свойствами характеристических функций:

,

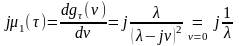откуда ;

,

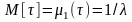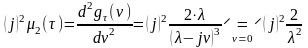откуда 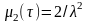и 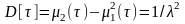. Значит, среднеквадратическое значение .

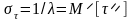При статистической обработке экспериментальных данных, когда возникает необходимость идентификации вида плотности распределения исследуемой случайной величины, последнее соотношение может служить одним из признаков экспоненциального распределения.

Сформированная таким образом математическая модель случайной последовательности событий называется простейшим потоком или потоком Пуассона и применяется в теории массового обслуживания и в теории надежности для вероятностного описания, например:

потока вызовов на телефонную станцию;

потока обращений к серверу коллективного пользования в компьютерной сети;

потока автомобилей на пограничный пункт таможенного досмотра;

потока клиентов на обслуживающее предприятие;

потока отказов технического устройства и т.д.

Наряду с простейшим потоком в теории массового обслуживания используются и более сложные модели потоков заявок, например, потоки Эрланга и Пальма, однако наиболее полные аналитические описания всех процедур и характеристик обслуживания заявок, потоков необслуженных заявок, длины очередей на обслуживание и тому подобных характеристик существуют пока только для простейших потоков.

В теории надежности F(t) называется функцией распределения времени безотказной работы устройства, а вероятность P(t) = 1 – F(t) = 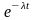– функцией надежности.

Математические модели случайных потоков событий применяются для анализа и синтеза систем, в которых подобные потоки возникают. Целью анализа и расчета таких систем может быть, например:

оценка вероятности того, что обслуживание заявки не состоится, и заявка пропадает;

оценка средней длины очереди заявок на обслуживание;

анализ и синтез стратегии обслуживания заявок;

расчет времени безотказной работы сложных систем и т.д.