
- •§ 1. Множества и операции над ними.
- •§ 5. Замечательные пределы и некоторые их свойства.
- •§ 2. Конечные и бесконечные множества.
- •§ 6. Вычисление пределов.
- •§ 3. Аксиоматика вещественных чисел.
- •§ 7. Сравнение функций.
- •§ 4. Некоторые свойства вещественных чисел.
- •4.1. Модуль вещественного числа и его свойства.
- •4.2. Ограниченные и неограниченные числовые множества.
- •4.3. Свойство Архимеда.
- •§ 1. Производная и дифференциал
- •§ 5. Расширенная система вещественных чисел. Некоторые числовые множества.
- •§ 2. Геометрический и физический смысл производной и дифференциала
- •§ 6. Принцип математической индукции.
- •§ 3. Дифференцирование суммы, произведения, частного
- •§ 1. Бесконечно малые и бесконечно большие последовательности.
- •§ 5. Производные и дифференциалы высших порядков
- •§ 2. Сходящиеся последовательности и их свойства.
- •§ 1. Теоремы о среднем
- •§ 4. Признаки существования пределов.
- •§ 2. Достаточные условия монотонности и экстремума функции на промежутке
- •§ 4. Подпоследовательности и предельные точки.
- •§ 3. Выпуклость, точки перегиба и асимптоты графика функции
- •§ 1. Функция, виды функций.
- •§ 4. Примерная схема исследования графика функции
- •§ 2. Предел функции.
- •§ 5. Правило Лопиталя
- •§ 3. Свойства пределов функции.
- •§ 6. Формулы Тейлора и Маклорена и некоторые их применения
- •I. Представление некоторых функций формулой Маклорена ( ):
- •§ 4. Признаки существования пределов.
- •§ 6. Формулы Тейлора и Маклорена и некоторые их применения
- •I. Представление некоторых функций формулой Маклорена ( ):
§ 5. Расширенная система вещественных чисел. Некоторые числовые множества.


 Приведем еще одну
геометрическую иллюстрацию вещественных
чисел. Рассмотрим числовую прямую и
окружность, касающуюся ее в точке О –
начале отсчета.
Приведем еще одну
геометрическую иллюстрацию вещественных
чисел. Рассмотрим числовую прямую и
окружность, касающуюся ее в точке О –
начале отсчета.
P
 -
+
-
+
x’
 x
0
x
0
Пусть ОР
- диаметр.
Построим отрезок Р ,
где точка
лежит на числовой прямой. Пусть
,
где точка
лежит на числовой прямой. Пусть
 -
точка пересечения отрезка Р
и окружности. Если исключить из
рассмотрения точку Р,
то между множеством точек
и множеством точек х
устанавливается
взаимно
однозначное соответствие,
т.е. каждой точке одного множества
отвечает единственная точка другого
множества, причем так, что различным
точкам отвечают также различные точки.
Дополним вещественную ось, а значит, и
множество вещественных чисел
-
точка пересечения отрезка Р
и окружности. Если исключить из
рассмотрения точку Р,
то между множеством точек
и множеством точек х
устанавливается
взаимно
однозначное соответствие,
т.е. каждой точке одного множества
отвечает единственная точка другого
множества, причем так, что различным
точкам отвечают также различные точки.
Дополним вещественную ось, а значит, и
множество вещественных чисел
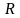 ,
двумя символами –
,
двумя символами – и
+
,
которые будут соответствовать точке Р
на окружности при рассмотренном правиле
взаимно однозначного соответствия.
и
+
,
которые будут соответствовать точке Р
на окружности при рассмотренном правиле
взаимно однозначного соответствия.
Определение 1.
Под расширенной
системой вещественных чисел
будем понимать множество
 =
=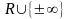 ,
для элементов которого выполняются
следующие условия:
,
для элементов которого выполняются
следующие условия:
1)
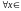 R:
–
<
R:
–
<
 <
+
,
<
+
,
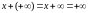 ,
,
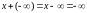 ,
,
 ;
;
2) если
>
0, то
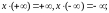
3) если
< 0, то
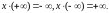
Если необходимо
подчеркнуть различие между символами
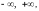 с одной стороны, и вещественными числами,
с другой, то последние будем называть
конечными. Если нас не интересует
знак, то будем писать символ
с одной стороны, и вещественными числами,
с другой, то последние будем называть
конечными. Если нас не интересует
знак, то будем писать символ
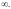
Заметим, что,
например, операции
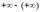 или
или
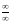 не определены (см. гл. II).
не определены (см. гл. II).
Определение 2. Пусть А . Если А не ограничено сверху, то будем полагать sup A = + ; если А неограниченно снизу, то inf A = - .
В дальнейшем мы будем оперировать следующими числовыми множествами:
1) сегмент, или
отрезок
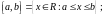
2) интервал
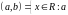 <
<
<
<
3)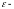 окрестность
точки
окрестность
точки

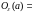
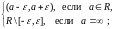
4) проколотая
окрестность
точки
:
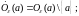
5) окрестность
точки
 :
:
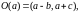 где
где
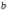 > 0,
> 0,
 >0;
>0;
полусегменты, или полуинтервалы :
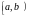 =
=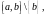 (
(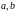 ]
= [
]
\ {
};
]
= [
]
\ {
};
числовая прямая :
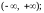
полупрямые : [
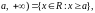
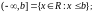
открытые полупрямые:
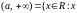 >
>
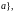
 <
<
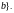
Все указанные множества, кроме 3) и 4), будем называть еще промежутками.
§ 2. Геометрический и физический смысл производной и дифференциала
Пусть функция
определена
в интервале (a, b)
и дифференцируема в точке
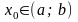 .
Пусть
.
Пусть
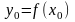 ,
,
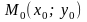 ,
,
 ,
,
 ,
,
 .
.
Рис.
1


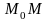 ( см. рис.1), уравнение которой
( см. рис.1), уравнение которой
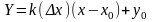 .
.
Здесь
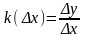 .
(1)
.
(1)
Так как функция
непрерывна
в точке
,
то
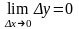 и, следовательно,
и, следовательно,

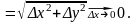
Рис.
2
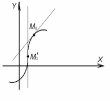
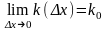 ,
то прямая
,
то прямая
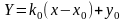 называется наклонной касательной
к графику функции
в
точке
называется наклонной касательной
к графику функции
в
точке
 ;
если
;
если
 то прямая
то прямая
 называется вертикальной касательной
к графику функции
в
точке
называется вертикальной касательной
к графику функции
в
точке
 (рис. 2).
(рис. 2).
По-другому,
предельное положение секущей
при
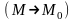 называется
касательной к графику функции
в
точке
.
называется
касательной к графику функции
в
точке
.
Теорема (о касательной). Пусть функция непрерывна в точке . В точке существует наклонная касательная тогда и только тогда, когда функция дифференцируема в точке . При этом ее уравнение имеет вид
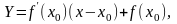 (2)
(2)
а
значит,
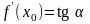 ,
где
,
где
 - угол наклона касательной к положительному
направлению оси
- угол наклона касательной к положительному
направлению оси
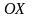 .
.
Доказательство.
В силу (1) конечное
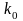 существует тогда и только тогда, когда
существует конечный предел
существует тогда и только тогда, когда
существует конечный предел
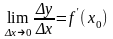 ,
причем
,
причем
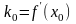 .
Отсюда и следует, что касательная в
точке
существует и ее уравнение имеет вид
(2). Из курса аналитической геометрии
.
Отсюда и следует, что касательная в
точке
существует и ее уравнение имеет вид
(2). Из курса аналитической геометрии
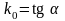 .
Поэтому
.
Поэтому
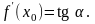
Следствие.
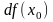 равен приращению ординаты касательной
в точке
.
равен приращению ординаты касательной
в точке
.
Действительно, первое слагаемое в (2) есть .
Вставка 1.
Рис.
3
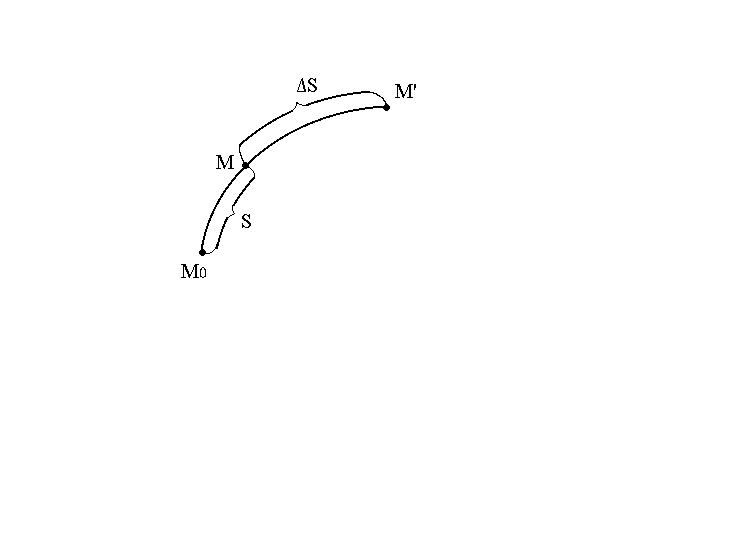
 -
закон движения материальной точки;
-
закон движения материальной точки;
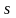 -
длина пути, отсчитываемая от точки
;
-
длина пути, отсчитываемая от точки
;
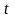 -
время, за которое пройден путь
.
Пусть
-
время, за которое пройден путь
.
Пусть
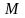 -
положение точки в момент времени
,
а
-
положение точки в момент времени
,
а
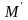 -
в момент времени
-
в момент времени
 ,
,
 -
длина пути
-
длина пути
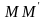 (рис. 3).
(рис. 3).
Тогда
 -
средняя скорость движения на участке
,
а
-
средняя скорость движения на участке
,
а
 =
=
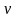 есть величина скорости движения
в точке
-
мгновенная скорость в точке
.
есть величина скорости движения
в точке
-
мгновенная скорость в точке
.
Таким образом,
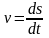 .
Отсюда
.
Отсюда
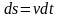 -
расстояние, которое прошла бы точка за
промежуток времени
-
расстояние, которое прошла бы точка за
промежуток времени
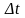 ,
если бы она двигалась равномерно со
скоростью, равной мгновенной скорости
в точке
.
,
если бы она двигалась равномерно со
скоростью, равной мгновенной скорости
в точке
.
Если
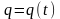 - количество электричества, протекающего
через поперечное сечение проводника
за время
,
то
- количество электричества, протекающего
через поперечное сечение проводника
за время
,
то
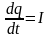 есть сила тока в момент
,
а
есть сила тока в момент
,
а
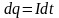 -
количество электричества за время
при
постоянной силе тока I.
-
количество электричества за время
при
постоянной силе тока I.
Билет № 6
1. Принцип математической индукции.
2. Дифференцирование суммы, произведения, частного.
