
- •§ 1. Множества и операции над ними.
- •§ 5. Замечательные пределы и некоторые их свойства.
- •§ 2. Конечные и бесконечные множества.
- •§ 6. Вычисление пределов.
- •§ 3. Аксиоматика вещественных чисел.
- •§ 7. Сравнение функций.
- •§ 4. Некоторые свойства вещественных чисел.
- •4.1. Модуль вещественного числа и его свойства.
- •4.2. Ограниченные и неограниченные числовые множества.
- •4.3. Свойство Архимеда.
- •§ 1. Производная и дифференциал
- •§ 5. Расширенная система вещественных чисел. Некоторые числовые множества.
- •§ 2. Геометрический и физический смысл производной и дифференциала
- •§ 6. Принцип математической индукции.
- •§ 3. Дифференцирование суммы, произведения, частного
- •§ 1. Бесконечно малые и бесконечно большие последовательности.
- •§ 5. Производные и дифференциалы высших порядков
- •§ 2. Сходящиеся последовательности и их свойства.
- •§ 1. Теоремы о среднем
- •§ 4. Признаки существования пределов.
- •§ 2. Достаточные условия монотонности и экстремума функции на промежутке
- •§ 4. Подпоследовательности и предельные точки.
- •§ 3. Выпуклость, точки перегиба и асимптоты графика функции
- •§ 1. Функция, виды функций.
- •§ 4. Примерная схема исследования графика функции
- •§ 2. Предел функции.
- •§ 5. Правило Лопиталя
- •§ 3. Свойства пределов функции.
- •§ 6. Формулы Тейлора и Маклорена и некоторые их применения
- •I. Представление некоторых функций формулой Маклорена ( ):
- •§ 4. Признаки существования пределов.
- •§ 6. Формулы Тейлора и Маклорена и некоторые их применения
- •I. Представление некоторых функций формулой Маклорена ( ):
§ 6. Формулы Тейлора и Маклорена и некоторые их применения
Пусть Pn
(x) – многочлен степени
n. Если функция
дифференцируема в точке
,
то, как было показано (гл. Y,
§ 1), ее можно представить в виде
 при
.
Поставим более общую задачу. Пусть
функция
имеет в точке
при
.
Поставим более общую задачу. Пусть
функция
имеет в точке
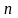 производных. Требуется выяснить,
существуют ли многочлены
производных. Требуется выяснить,
существуют ли многочлены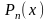 такие, что
такие, что
 при
,
и если да, то сколько их.
при
,
и если да, то сколько их.
Теорема 1 (формула Тейлора с остаточным членом в форме Пеано). Пусть функция раз дифференцируема в . Тогда при имеет место равенство
 ,
,
 .
(1)
.
(1)
Доказательство.
Положим
 .
Поскольку
.
Поскольку

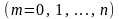 ,
то
,
то
 .
.
Поэтому,
применяя
 раз правило Лопиталя, получим
раз правило Лопиталя, получим
 ,
откуда
,
откуда
=
 при
,
т.е. получили (1).
при
,
т.е. получили (1).
Определение.
Многочлен называется
многочленом Тейлора в окрестности
точки
,
а при
называется
многочленом Тейлора в окрестности
точки
,
а при
 называется многочленом Маклорена,
формула (1) называется - формулой
Тейлора, а
- остаточным членом в форме Пеано.
называется многочленом Маклорена,
формула (1) называется - формулой
Тейлора, а
- остаточным членом в форме Пеано.
Вставка 1.
Теорема 2
(единственность разложения функции
по формуле Тейлора). Пусть функция
n раз дифференцируема
в
и
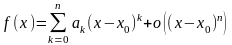 при
.
при
.
Тогда
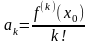
 ,
т.е. представление в данном виде
единственно.
,
т.е. представление в данном виде
единственно.
Доказательство. Из условия теоремы и формулы Тейлора получим равенство
 =
=
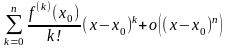 .
.
Переходя здесь к
пределу при
,
будем иметь
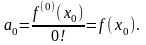 Если
теперь в предыдущем равенстве привести
подобные
Если
теперь в предыдущем равенстве привести
подобные
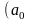 и
и
 ,
сократить полученный результат на
,
сократить полученный результат на
 и вновь перейти к пределу при
,
то получим
и вновь перейти к пределу при
,
то получим
 .
Продолжая этот процесс, получим
утверждение теоремы.
.
Продолжая этот процесс, получим
утверждение теоремы.
Вставка 2.
Теорема 3
(формула Тейлора с остаточным членом
в форме Лагранжа). Пусть функция
 раз дифференцируема в
.
Тогда найдется точка
,
лежащая между
и
такая, что
раз дифференцируема в
.
Тогда найдется точка
,
лежащая между
и
такая, что
 .
.
Доказательство.
Рассмотрим функцию
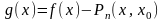 .
Тогда, как показано в теореме 1, выполнены
равенства
.
Тогда, как показано в теореме 1, выполнены
равенства
 .
Положим
.
Положим
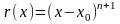 .
Для этой функции также имеем равенства
.
Для этой функции также имеем равенства
 .
Поэтому, применяя
раз теорему Коши (§ 1), получим, что
.
Поэтому, применяя
раз теорему Коши (§ 1), получим, что

 ,
лежащие между
и
,
лежащие между
и
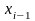 (при
(при
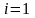 полагаем
=
)
такие, что
полагаем
=
)
такие, что
 .
.
Применим еще раз теорему Коши: найдется точка , лежащая между и xn , а значит, лежащая между и такая, что
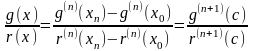 .
.
Отсюда окончательно имеем
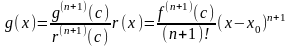 ,
,
что и требовалось доказать.
Вставка 3.
Рассмотрим некоторые приложения формулы Тейлора.
I. Представление некоторых функций формулой Маклорена ( ):
а) 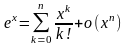 , б)
, б) 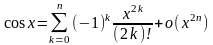 ,
,
в) 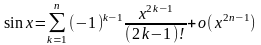 , г)
, г)
 ,
,
д)  .
.
Доказательство сразу вытекает из соотношений:
а) 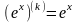 , б)
, б)  в)
в) 
г)  д)
д)  .
.
Вставка 4.
II. Третье достаточное условие локального экстремума. Пусть дана функция . Если из производных, не обращающихся в нуль в точке , первой оказывается производная нечетного порядка, то не является точкой локального экстремума. Если же такой производной является производная четного порядка, то - точка локального экстремума, причем точкой максимума, если эта производная отрицательна, и минимума, если эта производная положительна.
Действительно,
пусть
 ,
,
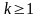 ,
- первая производная, отличная от нуля.
Запишем формулу Тейлора в следующем
виде
,
- первая производная, отличная от нуля.
Запишем формулу Тейлора в следующем
виде
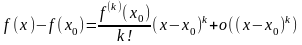 при
.
при
.
Ясно,
что при х, близких к х0,
 .
Поэтому при нечетном
.
Поэтому при нечетном
 этот знак меняется в зависимости от
полуокрестности, и потому экстремума
в точке
нет. При четном
знак не меняется, что и означает наличие
экстремума в точке
.
этот знак меняется в зависимости от
полуокрестности, и потому экстремума
в точке
нет. При четном
знак не меняется, что и означает наличие
экстремума в точке
.
Вставка 5.
III. Приближенные вычисления. При , близком к , из формулы Тейлора получим формулу для приближенных вычислений значения функции
 ,
,
причем за счет увеличения числа можно будет добиться наперед заданной точности вычислений (об этом более подробно будет изложено во второй части в теме «Ряды»).
Вставка 6.
IV..
Выделение главной части функции.
Из формулы Тейлора следует, что главная
часть функции f при
равна, например, первому слагаемому
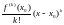 ,
отличному от нуля.
,
отличному от нуля.
Вставка 7.
Y.
Вычисление пределов основано
на формуле
 ~
~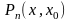 при
,
где
- многочлен Тейлора, что равносильно
замене функции f
ее главной частью при
.
при
,
где
- многочлен Тейлора, что равносильно
замене функции f
ее главной частью при
.
1. Признаки существования пределов функций.
2. Формула Маклорена и некоторые её применения.
