
- •§ 1. Множества и операции над ними.
- •§ 5. Замечательные пределы и некоторые их свойства.
- •§ 2. Конечные и бесконечные множества.
- •§ 6. Вычисление пределов.
- •§ 3. Аксиоматика вещественных чисел.
- •§ 7. Сравнение функций.
- •§ 4. Некоторые свойства вещественных чисел.
- •4.1. Модуль вещественного числа и его свойства.
- •4.2. Ограниченные и неограниченные числовые множества.
- •4.3. Свойство Архимеда.
- •§ 1. Производная и дифференциал
- •§ 5. Расширенная система вещественных чисел. Некоторые числовые множества.
- •§ 2. Геометрический и физический смысл производной и дифференциала
- •§ 6. Принцип математической индукции.
- •§ 3. Дифференцирование суммы, произведения, частного
- •§ 1. Бесконечно малые и бесконечно большие последовательности.
- •§ 5. Производные и дифференциалы высших порядков
- •§ 2. Сходящиеся последовательности и их свойства.
- •§ 1. Теоремы о среднем
- •§ 4. Признаки существования пределов.
- •§ 2. Достаточные условия монотонности и экстремума функции на промежутке
- •§ 4. Подпоследовательности и предельные точки.
- •§ 3. Выпуклость, точки перегиба и асимптоты графика функции
- •§ 1. Функция, виды функций.
- •§ 4. Примерная схема исследования графика функции
- •§ 2. Предел функции.
- •§ 5. Правило Лопиталя
- •§ 3. Свойства пределов функции.
- •§ 6. Формулы Тейлора и Маклорена и некоторые их применения
- •I. Представление некоторых функций формулой Маклорена ( ):
- •§ 4. Признаки существования пределов.
- •§ 6. Формулы Тейлора и Маклорена и некоторые их применения
- •I. Представление некоторых функций формулой Маклорена ( ):
§ 2. Достаточные условия монотонности и экстремума функции на промежутке
Теорема 1
(Достаточное и необходимое условие
монотонности). Для того, чтобы
дифференцируемая на интервале
функция
не убывала (не возрастала) на нем,
необходимо и достаточно, чтобы


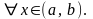
Доказательство.
1) Пусть, например,
Возьмем произвольные точки
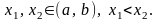 К отрезку
К отрезку
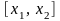 применим теорему Лагранжа:
применим теорему Лагранжа:
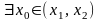 :
:
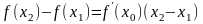 .
Так как
.
Так как
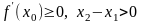 ,
то
,
то
 ,
что и означает не убывание функции
на
интервале
.
,
что и означает не убывание функции
на
интервале
.
Случай
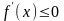 рассматривается аналогично.
рассматривается аналогично.
Пусть теперь функция дифференцируема и не убывает на интервале . Предположим, что
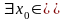 :
:
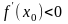 .
Так как
.
Так как
 ,
то по
,
то по
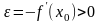
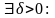
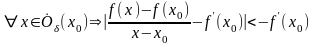 ,
или , в частности
,
или , в частности
 .
Отсюда при
получим
.
Отсюда при
получим
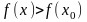 ,
а при
получим
,
а при
получим
 .
Таким образом, функция
убывает в
.
Таким образом, функция
убывает в
 ,
что противоречит условию. Следовательно,
,
что противоречит условию. Следовательно,
Так же, как в случае 1), доказывается
Теорема 2
(Достаточное условие строгой
монотонности). Если
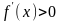
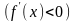 ,
то функция
возрастает (убывает) на интервале
,
то функция
возрастает (убывает) на интервале

Вставка 1.
Теорема 3 (1-е достаточное условие локального экстремума). Пусть - критическая точка непрерывной в и дифференцируемой в функции . Тогда, если функция меняет знак при переходе через точку ,то - точка локального экстремума функции , а именно: если меняет знак с "–" на "+", то - точка локального минимума; если меняет знак с "+" на "–" , то - точка локального максимума.
Доказательство. Пусть, например, меняет знак с "–" на "+", тогда по предыдущей теореме функция убывает слева от точки и возрастает справа от нее. А это и означает, что является точкой локального минимума.
Вставка 2.
Теорема 4 (2-е
достаточное условие локального
экстремума). Пусть функция
дифференцируема в интервале
,
,
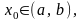 и
и
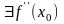 .
Тогда:
.
Тогда:
а) если
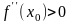 ,
то
- точка локального минимума функции
;
,
то
- точка локального минимума функции
;
б) если
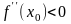 ,
то
- точка локального максимума функции
.
,
то
- точка локального максимума функции
.
Доказательство.
Пусть
,
т.е.
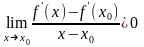 .
Тогда
.
Тогда
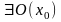 такая, что
такая, что
 .
.
Если теперь
,
то
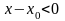 и потому
и потому
 ;
если же
,
то
;
если же
,
то
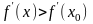 .
А так как
,
то при переходе через точку
производная функции меняет знак с "–"
на "+",
т.е.
-
точка локального минимума функции
.
.
А так как
,
то при переходе через точку
производная функции меняет знак с "–"
на "+",
т.е.
-
точка локального минимума функции
.
Аналогично рассматривается случай .
Вставка 3.
Рассмотрим вопрос о нахождении наибольшего и наименьшего значений непрерывной на отрезке функции.
По теореме Вейерштрасса такие значения существуют и достигаются на нем. Если, например, наибольшее значение реализуется во внутренней точке отрезка, то это необходимо есть точка локального экстремума (максимума). Поэтому для нахождения наибольшего и наименьшего значений непрерывной на отрезке функции находят ее критические точки на данном отрезке, вычисляют в них значения функции (не обязательно выясняя наличие экстремума) , добавляют к ним значения функции в концах отрезка и выбирают из них наибольшее и наименьшее.
.
Билет № 10
1. Последовательности и предельные точки.
2. Выпуклость, точки перегиба и асимптоты графика функции.
