
- •§ 1. Множества и операции над ними.
- •§ 5. Замечательные пределы и некоторые их свойства.
- •§ 2. Конечные и бесконечные множества.
- •§ 6. Вычисление пределов.
- •§ 3. Аксиоматика вещественных чисел.
- •§ 7. Сравнение функций.
- •§ 4. Некоторые свойства вещественных чисел.
- •4.1. Модуль вещественного числа и его свойства.
- •4.2. Ограниченные и неограниченные числовые множества.
- •4.3. Свойство Архимеда.
- •§ 1. Производная и дифференциал
- •§ 5. Расширенная система вещественных чисел. Некоторые числовые множества.
- •§ 2. Геометрический и физический смысл производной и дифференциала
- •§ 6. Принцип математической индукции.
- •§ 3. Дифференцирование суммы, произведения, частного
- •§ 1. Бесконечно малые и бесконечно большие последовательности.
- •§ 5. Производные и дифференциалы высших порядков
- •§ 2. Сходящиеся последовательности и их свойства.
- •§ 1. Теоремы о среднем
- •§ 4. Признаки существования пределов.
- •§ 2. Достаточные условия монотонности и экстремума функции на промежутке
- •§ 4. Подпоследовательности и предельные точки.
- •§ 3. Выпуклость, точки перегиба и асимптоты графика функции
- •§ 1. Функция, виды функций.
- •§ 4. Примерная схема исследования графика функции
- •§ 2. Предел функции.
- •§ 5. Правило Лопиталя
- •§ 3. Свойства пределов функции.
- •§ 6. Формулы Тейлора и Маклорена и некоторые их применения
- •I. Представление некоторых функций формулой Маклорена ( ):
- •§ 4. Признаки существования пределов.
- •§ 6. Формулы Тейлора и Маклорена и некоторые их применения
- •I. Представление некоторых функций формулой Маклорена ( ):
Билет № 1
1. Множества и операции над ними.
2. Замечательные пределы и некоторые их свойства.
§ 1. Множества и операции над ними.
Для удобства записей в дальнейшем будем использовать символы:
А – «для любого (произвольного) А»;
В – «существует (найдется) В»;
А В (импликация) – «В следует из А», «В – необходимое условие для А», «А – достаточное условие для В»;
А В – «В является необходимым и достаточным условием для А»; «А имеет место тогда и только тогда, когда выполнено В»;
А В – «А и В справедливы одновременно»;
А В – «справедливо хотя бы одно из предложений А или В».
Понятие множества относится к начальным понятиям современной математики. Оно не сводится к другим, уже известным и потому более простым понятиям, а значит, его нельзя определить, не используя синонимы, а можно только описать.
Под множеством будем понимать собрание, совокупность некоторых предметов, понятий, объединенных по какому-либо признаку (условию).
Вставка 1.
Предметы или понятия, составляющие некоторое множество, называются его элементами (иногда, точками).
Множества будем обозначать либо заглавными буквами А, В,…, либо прописными в фигурных скобках {x}, {a},... Множество элементов, обладающих характерным свойством Р, будем записывать так А = {x| P}.
Вставка 2.
В дальнейшем: N – множество натуральных чисел, Z – множество целых чисел, Q – множество рациональных чисел, J – множество иррациональных чисел, R – множество вещественных (действительных) чисел.
Если элемент х принадлежит множеству А, то будем писать х А; если же х не принадлежит А, то будем писать х А.
Начальным понятием является также понятие пустого множества, т.е. множества, не содержащее элементов. Пустое множество будем обозначать символом .
Множество А называется подмножеством множества В, если х А х В. В этом случае пишут А В. Пустое множество считают подмножеством любого множества А.
Возможен случай А = В, т.е. элементы множеств А и В совпадают.
Вставка 3.
Суммой или объединением А В множеств А и В называется множество С, состоящее из элементов, принадлежащих хотя бы одному из множеств А или В (С = А В = {x| х А х В}).
Вставка 4.
Из приведенного определения суммы вытекает, что А В = В А, А (В С) = А (В С).
Пересечением А В двух множеств А и В называется множество D, составленное из элементов, принадлежащих как множеству А, так и множеству В (D = А В = {x | x A x B}).
Вставка 5.
Легко убедиться в справедливости следующих свойств: 1) А В = В А, 2) (А В) С = А (В С), 3) А В, то А В = А, в частности А А = А, А = .
Разностью Е = А \ В двух множеств А и В называется множество, состоящее из элементов множества А, не принадлежащих В. Если А S, то множество K = S \ А называется дополнением множества А до множества S.
§ 5. Замечательные пределы и некоторые их свойства.

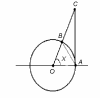

Доказательство.
Рассмотрим круг радиуса R с центром
в точке О. Пусть
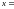
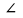 ВОА
, 0 < х <
ВОА
, 0 < х <
 и СА
и СА ОА
(см. рис.). Тогда
ОА
(см. рис.). Тогда
 ,
,
 ,
,
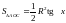 .
Из геометрических соображений получим
.
Из геометрических соображений получим
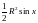 <
<
 <
<
 ,
откуда в результате преобразований
имеем неравенства 0 < 1 -
,
откуда в результате преобразований
имеем неравенства 0 < 1 -
 < 1 -
< 1 -
 .
.
В силу четности
здесь всех функций эти неравенства
можно считать верными
 .
.
Из левого неравенства
следует, что
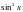 <
<
 ,
и потому
,
и потому
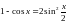 <
<
 .
Таким образом,
.
Таким образом,
0
< 1-
<
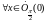 .
.
А так как
 ,
то из теоремы о зажатой функции получим
,
то из теоремы о зажатой функции получим
Вставка 1.
Следствие. 1)
 ,
2)
,
2)
 ,
3)
,
3)
 ,
4)
,
4)
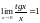 ,
,
5)
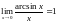 ,
6)
,
6)
 ,
7)
,
7)
 .
.
Доказательство.
1)
 ;
;
2)
0 <

 ;
;
3)
 ;
;
4)
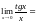
 ;
5)
;
5)
 ;
;
6)
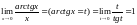 ;
7)
;
7)
 .
.
Теорема 2 (2-й
замечательный передел).
 .
.
Доказательство.
В § 3 гл. II
был доказан предел
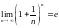 .
.
Пусть х +. Возьмем x > 1. По свойству Архимеда n N такое, что n х < n + 1. Тогда
 .
.
Так
как
 ,
то по теореме о зажатой функции получим
нужное.
,
то по теореме о зажатой функции получим
нужное.
2) Пусть х . Рассмотрим х < 1. Тогда

 .
.
Теорема доказана.
Следствие.
1)
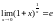 2)
2)

 (в частности,
(в частности,
 );
3)
);
3)
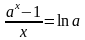
 (в частности,
(в частности,
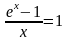 );
);
4)
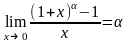 ;
5)
;
5)
 .
.
Действительно:
1)
 .
.
2) Воспользуемся
примером
 ,
тождеством
,
тождеством
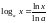 и теоремой о пределе сложной функции:
и теоремой о пределе сложной функции:
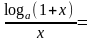

3)

4)

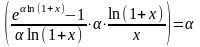 .
.
5)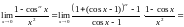
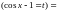
 .
.
Билет № 2
1. Конечные и бесконечные множества.
2. Вычисление пределов.
