17. Экспоненциальный (показательный) закон распределения.

Определение: Непрерывная случайная величина X, функция плотности которой задается выражением

называется случайной величиной, имеющей показательное, или экспоненциальное, распределение.

Величина срока службы различных устройств и времени безотказной работы отдельных элементов этих устройств при выполнении определенных условий обычно подчиняется показательному распределению. Другими словами, величина промежутка времени между появлениями двух последовательных редких событий подчиняется зачастую показательному распределению.

Как видно из формулы , показательное распределение определяется только одним параметром m.

Найдем функцию распределения показательного закона, используя свойства дифференциальной функции распределения:

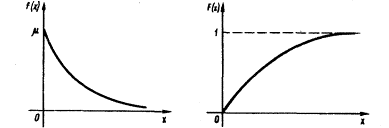
Графики дифференциальной и интегральной функций показательного распределения имеют вид:

18. Многомерная с.В.Ковариация…матрица Многоме́рное норма́льное распределе́ние

Многомерная случайная величина - упорядоченный набор (вектор) фиксированного числа одномерных случайных величин. Многомерное наблюдение  — реализация м.с.в. Как правило . Многомерная выборка  — неупорядоченный набор фиксированного числа многомерных наблюдений. Основными числовыми характеристиками м.с.в. являются вектор средних и ковариационная матрица.

Вектор средних

Вектор средних — вектор математических ожиданий м.с.в. . Оценкой вектора средних по многомерной выборке является среднее значение реализаций м.с.в.

.

Ковариационная матрица

Пусть случайные величины — элементы м.с.в. — имеют конечные дисперсии. Ковариационной матрицей м.с.в. называется квадратная матрица

в которой элементы  — ковариации случайных величин и . На главной диагнали матрицы находятся дисперсии случайных величин . Оценкой ковариационной матрицы по многомерной выборке является

.

Корреляционная матрица

Корреляционная матрица — матрица коэффициентов корреляции нескольких случайных величин с ненулевыми дисперсиями

в которой элементы есть коэффициенты корреляции соответствующих случайных величин. Диагональные элементы матрицы равны единице. Справедливо соотношение , где  — диагональная матрица с элементами .

Многоме́рное норма́льное распределе́ние (или многоме́рное га́уссовское распределе́ние) в теории вероятностей — это обобщение одномерного нормального распределения.

Определение Случайный вектор имеет многомерное нормальное распределение, если выполняется одно из следующих эквивалентных условий:

Произвольная линейная комбинация компонентов вектора имеет нормальное распределение или является константой.

Существует вектор независимых стандартных нормальных случайных величин , вещественный вектор и матрица размерности , такие что: .

Существует вектор и неотрицательно определённая симметричная матрица размерности , такие что характеристическая функция вектора имеет вид:

.