13. Интегральная теорема Лапласа. Кривая Гаусса.

   Теорема. Пусть производится n независимых опытов, в каждом из которых вероятность наступления события А одна и та же и равна . Пусть m - число появления события A в n опытах. Тогда для достаточно больших n случайная величина m имеет распределение, близкое к нормальному с параметрами a=M(m)=np, .

Следствия из интегральной теоремы Муавра-Лапласа

Пусть выполнены условия применимости интегральной теоремы Муавра-Лапласа.

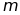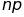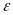Следствие 1. Вероятность того, что число наступлений события А в n повторных независимых испытаниях будет отличаться от величины не более чем на (по абсолютной величине), вычисляется по формуле

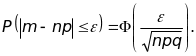
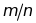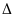Следствие 2. Вероятность того, что доля наступлений события А в n повторных независимых испытаниях будет отличаться от вероятности p наступления этого события в одном испытании не более чем на (по абсолютной величине), вычисляется по формуле

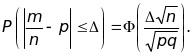
Кривая Гаусса.

Нормальным называют распределение вероятностей непрерывной случайной величины, которое задается плотностью . Нормальное распределение задается двумя параметрами: a – математическим ожиданием, – средним квадратическим отклонением. График плотности нормального распределения называют нормальной кривой (кривой Гаусса). Нормированным называют нормальное распределение с параметрами . Плотность нормированного распределения задается формулой .

Свойства. Если случайные величины и независимы и имеют нормальное распределение с математическими ожиданиями и и дисперсиями и соответственно, то также имеет нормальное распределение с математическим ожиданием и дисперсией .

13. (Продолжение) Функция Лапласа.

Найдем вероятность попадания случайной величины, распределенной по нормальному закону, в заданный интервал. Обозначим Тогда 

Т.к. интеграл  не выражается через элементарные функции, то вводится в рассмотрение функция , которая называется функцией Лапласа или интегралом вероятностей. Значения этой функции при различных значениях х посчитаны и приводятся в специальных таблицах. Ниже показан график функции Лапласа

.

 

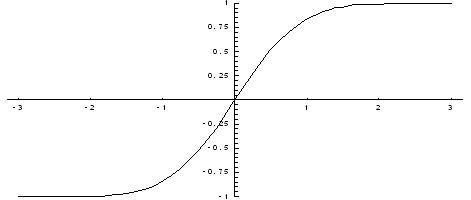
Функция Лапласа обладает следующими свойствами: 1) Ф(0) = 0; 2) Ф(-х) = - Ф(х); 3) Ф¥) = 1. Функцию Лапласа также называют функцией ошибок и обозначают erf x. Еще используется нормированная функция Лапласа, которая связана с функцией Лапласа соотношением:

14.Матожидание и дисперсия с.В. Моменты н-го порядка

Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности.

Если дискретная случайная величина принимает только значения x₁, x₂, ..., x_n, вероятности которых соответственно равны p₁, p₂, ..., p_n . Тогда математическим ожидание определяется равенством:

M (X) = x1p1 + x2p2 + ...+ xnpn.

Если дискретная случайная величина принимает счетное множество возможных значений, то

Дисперсией (рассеянием) дискретной случайной величины называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:

D (X) = M [X - M (X)]2.

Для вычисления дисперсии часто бывает удобно пользоваться следующей теоремой.

Теорема. Дисперсия равна разности между математическим ожиданием квадрата случайной величины Х и квадратом ее математического ожидания:

D (X) = M (X2) - [M (X)]2

Моменты n-го (k-го) порядка. Заменить k на n!

В теории вероятностей и математической статистике, помимо математического ожидания и дисперсии, используются и другие числовые характеристики случайных величин. В первую очередь это начальные и центральные моменты.

Начальным моментом k-го порядка случайной величины x называется математическое ожидание k-й степени случайной величины x , т.е. a _k = Mx ^k.

Центральным моментом k-го порядка случайной величины x называется величина m _k, определяемая формулой m _k = M(x - Mx )^k.

Заметим, что математическое ожидание случайной величины - начальный момент первого порядка, a ₁ = Mx , а дисперсия - центральный момент второго порядка,

a ₂ = Mx ² = M(x - Mx )² = Dx .

Существуют формулы, позволяющие выразить центральные моменты случайной величины через ее начальные моменты, например:

m ₂=a ₂-a ₁², m ₃ = a ₃ - 3a _{2a 1} + 2a ₁³.

Если плотность распределения вероятностей непрерывной случайной величины симметрична относительно прямой x = Mx , то все ее центральные моменты нечетного порядка равны нулю.