7. Условная вероятность и правило умножения для зависимых событий.

Условная вероятность — вероятность одного события при условии, что другое событие уже произошло.*Р_В(А)=Р(АВ)/Р(В) – условная вероятность А при условии В. (А произойдет если произойдет В).

*Р_А(В)=Р(АВ)/Р(А)

*Р(АВ)=Р(В)*Р_В(А)=Р(А)*Р_А(В).

Частный случай Р_В(А)=Р(А) то А и В – независимы для независимых событий Р(АВ)=Р(А)*Р(В)

8. Формула полной вероятности и Байеса.

Пусть событие А может появиться вместе с одним из образующих полную группу попарнонесовместных событий Н₁,Н₂…Н_n называемых гипотезами, тогда вероятность события А вычисляется как сумма произведений вероятностей каждой гипотезы на вероятность события А при этой гипотезе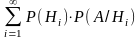

Формула Бейса Пусть имеется полная группа попарнонесовместных гипотез Н₁,Н₂…Н_nс известными вероятностями появления. В результате проведения опыта появилось некоторое события А, требуется переоценить вероятности гипотез при условии, что событие А произошло

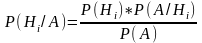
9. Случайная величина. Закон распределения и функция распределения.

Случайная величина в теории вероятностей, величина, принимающая в зависимости от случая те или иные значения с определёнными вероятностями. Так, число очков, выпадающее на верхней грани игральной кости, представляет собой С. в., принимающую значения 1, 2, 3, 4, 5, 6 с вероятностью ¹/₆ каждое. Если С. в. Х принимает конечную или бесконечную последовательность различных значений, то её распределение вероятностей (закон распределения) задаётся указанием этих значений:

x₁, x₂,..., x_n,...

и соответствующих им вероятностей:

p₁, p₂,..., p_n....

С. в. указанного типа называются дискретными. В других случаях распределение вероятностей задаётся указанием для каждого отрезка D = [а, b] вероятности Р_х (а, b)неравенства а £ х < b. Особенно часто встречаются С. в., для которых существует такая функция p_x (x)(плотность вероятности), что

С. в. этого типа называются непрерывными.

Ряд общих свойств распределения вероятностей С. в. достаточно полно описывается небольшим количеством числовых характеристик. Наиболее употребительными среди этих последних являются математическое ожидание Ех С. в. Х и её дисперсия Dx. Менее употребительны медиана, мода, квантили и т. п.

Законом распределения случайной величины называется соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями (его можно задать таблично, аналитически (в виде формулы) и графически.

При табличном задании закона распределения дискретной случайной величины первая строка таблицы содержит возможные значения, а вторая - их вероятности (Табл.1).

Таблица 1

Х	х1	х2	...	хn
p	p1	p2	...	pn

Сумма вероятностей второй строки таблицы 1, равна единице:

p₁ + p₂ + ...+ p_n = 1.

Функция распределения случайной величины. Её свойства

Каждая случайная величина полностью определяется своей функцией распределения.

Если x .- случайная величина, то функция F(x) = F_x (x) = P(x < x) называется функцией распределения случайной величины x . Здесь P(x < x) - вероятность того, что случайная величина x принимает значение, меньшее x.

Функция распределения любой случайной величины обладает следующими свойствами:

F(x) определена на всей числовой прямой R;

F(x) не убывает, т.е. если x₁ x₂, то F(x₁) F(x₂);

F(- )=0, F(+ )=1, т.е. и ;

F(x) непрерывна справа, т.е.