2. Ядро и образ линейного оператора

Пусть дан линейный оператор действующий из линейного пространства в линейное пространство Следующие понятия бывают полезными при решении линейных уравнений.

Определение 1. Ядром оператора называется множество

Образом оператора называется множество

Нетрудно доказать следующее утверждение.

Теорема 3. Ядро и образ линейного оператора являются линейными подпространствами пространств и соответственно, причем имеет место равенство

Для вычисления ядра оператора надо записать уравнение в матричной форме (выбрав базисы в пространствах и соответственно) и решить соответствующую алгебраическую систему уравнений. Поясним теперь, как можно вычислить образ оператора .

Пусть матрица оператора в в базисах и Обозначим через -й столбец матрицы Принадлежность вектора образу означает, что существуют числа такие, что вектор столбец представляется в виде т.е. является элементом пространства линейных комбинаций столбцов матрицы Выбрав в этом пространстве базис (например, максимальную совокупность линейно независимых столбцов матрицы ), вычислим сначала образ оператора-матрицы : а затем построим образ оператора :

1. Билет 27 Изменение координат вектора и матрицы оператора при переходе к новому базису

Пусть линейный оператор , действует из пространства в себя и пусть в линейном пространстве выбраны два базиса: и Разложим “новые” базисные вектора в линейные комбинации “старых” базисных векторов :

Стоящая здесь матрица м столбцом которой является координатный столбец го базисного вектора в “старом” базисе называется матрицей перехода от “старого”базиса к “новому“. Если теперь координаты вектора в “старом” базисе а координаты того же вектора в “новом” базисе то имеет место равенство

Так как разложение по базису единственно, то отсюда следует, что

Получен следующий результат.

Теорема 1. Координаты вектора в базисе и координаты того же вектора в базисе связаны соотношениями (2), где матрица перехода от “старого”базиса к “новому“ .

Посмотрим теперь, как связаны между собой матрицы и одного и того же оператора в различных базисах и пространства Матрицы и определяются равенствами Пусть Это равенство в базисе равносильно матричному равенству

а в базисе матричному равенству ( здесь приняты те же обозначения, что и в (1)). Используя теорему (1), будем иметь

так как столбец произвольный, то отсюда получаем равенство

Доказан следующий результат.

Теорема 2. Если матрица оператора в базисе а матрица того же оператора в базисе то

Замечание 1. Две произвольные матрицы и связанные соотношением где некоторая невырожденная матрица называются подобными матрицами. Таким образом, две матрицы одного и того же оператора в различных базисах подобны.

Пример 1. Матрица оператора в базисе имеет вид

Найти матрицу этого оператора в базисе Вычислить координаты вектора в базисе

Решение. Матрица перехода от старого базиса к новому и обратная к ней матрица имеют вид

поэтому по теореме 2 матрица оператора и новом базисе будет такой:

Далее, вектор имеет следующий координатный столбец в базисе По теореме 1 координатный столбец этого вектора в базисе будет иметь вид

Замечание 2. Можно обобщить этот результат на операторы, действующие из одного линейного пространства в другое. Пусть оператор действует из линейного пространства в другое линейное пространство и пусть в пространстве выбраны два базиса: и а в пространстве – два базиса и Тогда можно составить две матрицы и линейного оператора

и две матрицы и перехода от “старых” базисов к “новым”:

Нетрудно показать, что в этом случае имеет место равенство

Билет 28 Собственные значения и собственные векторы линейного оператора. Матрица оператора в базисе из собственных векторов

Пусть дан линейный оператор ( линейное пространство над числовом полем ⁴ ).

Определение 2. Вектор называется собственным вектором, соответствующим собственному значению , если: а) б) Совокупность всех различных собственных значений оператора называют спектром оператора . Обозначение:

В качестве обычно берут множество действительных чисел или множество комплексных чисел

Например, если матрица то вектор является собственным вектором этого оператора, соответствующим собственному значению так как При этом

Отметим очевидное свойство собственных векторов: если собственный вектор оператора соответствующий собственному значению то тоже собственный вектор оператора соответствующий собственному значению В ряде случаев, выбирая постоянную можно упростить вид собственных векторов.

Опишем теперь, как вычисляются собственные векторы и собственные значения. Зафиксируем в пространстве некоторый базис и вычислим матрицу оператора в этом базисе. Тогда операторное уравнение (с учетом того, где ) можно записать в матричном виде

Эта система должна иметь нетривиальное решение поэтому ее определитель должен равняться нулю

Определитель (5) называется характеристическим определителем матрицы (или оператора ). Раскрывая его, получим так называемое характеристическое уравнение , решая которое, найдем собственные значения матрицы ( или оператора ) . Положив в (4) и решив полученную алгебраическую систему уравнений относительно вектора-столбца , найдем все собственные векторы соответствующие собственному значению матрицы Затем по формуле вычислим собственные векторы оператора , соответствующие собственному значению

Билет 29 Кривые второго порядка на плоскости

Множество точек на плоскости⁵ удовлетворяющих уравнению

где не обращаются одновременно в нуль, называется кривой второго порядка на плоскости. Старшие члены в (2) образуют действительную квадратичную форму

с матрицей По теореме 4 ортогональным преобразованием (где матрица из ортонормированных собственных векторов матрицы ) ее можно привести к каноническому виду , где собственные значения матрицы При этом преобразовании исходное уравнение (2) приводится к виду

Применяя метод выделения полного квадрата Лагранжа, преобразуем уравнение (4) к одной из следующих форм (ради удобства записываем эти уравнения в терминах исходных переменных и ):

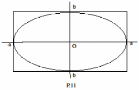
1. (эллипс с полуосями и )

2. (гипербола с полуосями и )

Рис. 12

Метод сечений. Суть этого метода состоит в том, что одну из переменной в уравнении поверхности фиксируют (например, считают постоянной) и затем смотрят, какая кривая второго порядка получилась в сечении . Например, рассмотрим уравнение двуполостного гиперболоида Таблица 1. Поверхности второго порядка

Зафиксируем здесь переменную После преобразований получим следующее уравнение:

Это уравнение есть уравнение эллипса в плоскости с полуосями

и ,

1 Здесь и всюду далее с тем, чтобы не прерывать выкладки, в квадратных скобках будем указывать соответствующие замены переменных или формулы, необходимые для преобразований исходных выражений.

2 Полезно запомнить, что в первый индекс номер строка, а номер столбца, на пересечении которых находится элемент

3 Если оператор линейный, то пишут опуская скобки.

4

5 Эту плоскость мы будем обозначать так же, как и множество геометрических векторов, буквой .