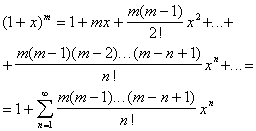VM2_1
.docБилет №1
Последовательность — это упорядоченный список элементов некоторого множества.
Часто
для обозначения последовательностей
используется индексная запись. Конечная
последовательность обозначается ![]() ,
а бесконечная
,
а бесконечная ![]() .
.
Примеры:
Целочисленная последовательность xn = ( − 1)n;
Функциональная последовательность
 ,
где
,
где
![]()
В математике пределом последовательности называют объект, к которому члены последовательности в некотором смысле стремятся или приближаются с ростом номера.
Пусть
дано топологическое пространство T и
последовательность xn.
Тогда, если существует элемент ![]() такой,
что
такой,
что
![]() ,
,
где U(x) — открытое множество, содержащее x, то он называется пределом последовательности xn.
Не у всякой последовательности существует предел. Например, если взять в качестве пространства множество вещественных чисел со стандартной топологией, а в качестве xn последовательность xn = ( − 1)n, то у неё не будет предела. Если у последовательности существует предел, то она называется сходящейся, если нет — расходящейся.
Пределом последовательности вещественных чисел называется число A, если выполнено следующее условие:
![]() ,
,
то есть для любой окрестности точки A можно указать номер, начиная с которого все элементы последовательности будут лежать в этой окрестности.
Имеют место следующие арифметические свойства пределов вещественных последовательностей:
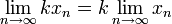 ,
где k — константа;
,
где k — константа;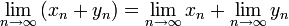 ,
если указанные пределы существуют;
,
если указанные пределы существуют;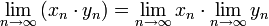 при
том же условии;
при
том же условии;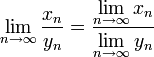 ,
если пределы существуют и
,
если пределы существуют и 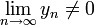 .
.
Билет №2
Определение ряда и его сходимость |
||
Определение 1. Пусть задана бесконечная числовая последовательность u1, u2,…,un,…. Выражение
называется числовым рядом. Числа u1, u2,…,un,… называются первым, вторым, …, n-м, … членами ряда. un также называется общим членом ряда. Сумма конечного числа n первых членов ряда называется n-ой частичной суммой ряда:
Если
существует конечный предел Ряд, полученный отбрасыванием от исходного n первых членов, называется n-м остатком ряда. Обозначение:
Все члены, кроме тех, что входят в n-й остаток ряда, в сумме дают т. н. n-ю частичную сумму ряда. Необходимое условие сходимости Для
сходимости ряда Док-во:
По условию последовательность
Если
ряды
Билет №3 Если an ≥ 0 (n = 1, 2, 3, ... ), то ряд a1 + a2 + a3 + ... называется положительным. В том случае, когда при всех n оказывается an > 0, будем называть ряд строго положительным. Положительные ряды обладают многими свойствами, сближающими их с обычными суммами конечного числа слагаемых. Легко видеть, что частичная сумма Sn = a1 + a2 + ... + an положительного ряда возрастает (может быть, не строго) с увеличением n. Так как всякая возрастающая числовая последовательность имеет конечный или бесконечный предел (причем члены последовательности не превосходят этого предела), то для любого положительного ряда существует предел
Этот предел будет конечным или бесконечным, смотря по тому, ограничено сверху или нет множество частичных сумм {Sn}. Таким образом, имеет место Теорема 1. Положительный ряд сходится тогда и только тогда, когда множество его частичных сумм ограничено сверху. Разумеется, у ряда не положительного ограниченность множества частичных сумм не обеспечивает сходимости, как это видно из примера ряда 1 + (-1) + 1 + (-1) + ... Отметим еще, что частичные суммы сходящегося положительного ряда не превосходят его суммы. Сходимость или расходимость ряда устанавливается с помощью достаточных признаков. Признаки сравнения рядов Даны
два ряда Если сходится, то также сходится; Если расходится, то также расходится. Предельные признаки сравнения рядов Пусть даны два ряда и , у которых члены an и bn положительны для всех n. Тогда справедливы следующие предельные признаки:
Так
называемый обобщенный
гармонический ряд
Билет №4 Ряд называется знакочередующимся, если его члены попеременно принимают значения противоположных знаков, т. е.:
Признак Лейбница — признак сходимости знакочередующегося ряда. Пусть для ряда
выполняются следующие условия:
Тогда этот ряд сходится. Ряды, удовлетворяющие признаку Лейбница, называются рядами Лейбница. Из доказательства признака Лейбница следует, что сумма знакопеременного сходящегося ряда меньше по модулю первого члена ряда. Поскольку любой остаток ряда rn является также рядом Лейбница, то для него справедливо:
Ряд абсолютно сходится, если сходится ряд, составленный из модулей членов этого ряда. Если ряд сходится, но не является абсолютно сходящимся, то он называется условно сходящимся. абсолютная сходимость «сильнее» «простой» сходимости.
Билет №5. Определение. Ряд, члены которого являются функциями, называется функциональным рядом. Его обозначают:
Определение.
Если при Определение.
Множество всех значений Очевидно,
что в области сходимости функционального
ряда его сумма является функцией от
.
Будем ее обозначать Признак Вейерштрасса. Теорема.
Если для функционального ряда Док-во По
условию (2) для любого n
,
любого p Из (3) и (4) следует, что для ряда (1) вып. Условие Коши на множестве Е, в силу этого по критерию Коши — ряд сходится равномерно на множестве Е. Абсолютная сходимость ряда для каждого следует из правой части (3). Следствие:
Если сходится ряд
,
где
Теорема. Если все члены ряда (1) - непрерывные на [a;b] ф-ции, а ряд (1) сх-ся равномерно на [a;b], то его сумма S(x) также непрерывна на отрезке [a;b].
Т
е о р е м а 1. Пусть на отрезке
равномерно
на
Т е о р е м а 2. Равномерно сходящийся на отрезке ряд (комплекснозначных) непрерывных функций
можно
почленно интегрировать
Полученный при этом ряд (4) равномерно сходится на . В частности,
Дифференцирование походу тоже самое что и интегрирование только наоборот. , (8)
|
Билет №6
Степенной ряд с одной переменной — это формальное алгебраическое выражение вида:
![]()
в
котором коэффициенты ![]() берутся
из некоторого кольца
берутся
из некоторого кольца ![]() .
.
Признаки сходимости
Для степенных рядов есть несколько теорем, описывающих условия и характер их сходимости.
Первая теорема Абеля: Пусть ряд
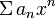 сходится
в точке
сходится
в точке 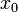 .
Тогда этот ряд сходится абсолютно в
круге
.
Тогда этот ряд сходится абсолютно в
круге 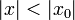 и
равномерно по
и
равномерно по 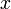 на
любом компактном подмножестве этого
круга.
на
любом компактном подмножестве этого
круга.
Обращая
эту теорему, получаем, что если степенной
ряд расходится при ![]() ,
он расходится при всех
,
таких что
,
он расходится при всех
,
таких что ![]() .
Из первой теоремы Абеля также следует,
что существует такой радиус круга
(возможно,
нулевой или бесконечный), что при
.
Из первой теоремы Абеля также следует,
что существует такой радиус круга
(возможно,
нулевой или бесконечный), что при ![]() ряд
сходится абсолютно (и равномерно по
на
компактных подмножествах круга
),
а при
ряд
сходится абсолютно (и равномерно по
на
компактных подмножествах круга
),
а при ![]() —
расходится. Это значение
называется
радиусом сходимости ряда, а круг
—
кругом сходимости.
—
расходится. Это значение
называется
радиусом сходимости ряда, а круг
—
кругом сходимости.
Формула Коши-Адамара: Значение радиуса сходимости степенного ряда может быть вычислено по формуле:
![]()
Признак Д’Аламбера: Если при
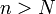 и
и 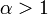 выполнено
неравенство
выполнено
неравенство

тогда
степенной ряд
сходится
во всех точках окружности ![]() абсолютно
и равномерно по
.
абсолютно
и равномерно по
.
Вторая теорема Абеля: Пусть степенной ряд сходится в точке . Тогда он сходится равномерно по на отрезке, соединяющем точки 0 и .
Интервал сходимости степенного ряда |
Так называется интервал, в каждой точке которого степенной ряд с действительными членами сходится, причем абсолютно. На каждом из концов этого интервала ряд может как сходиться (абсолютно или условно), так и расходиться. Вне этого интервала ряд расходится. Заметим, что интервал сходимости существует для каждого сходящегося хоть на каком-нибудь интервале степенного ряда. Для ряда, сходящегося только в одной точке, интервал получается вырожденным. Для расходящегося ряда интервал равен пустому множеству. |
Рассмотрим
степенной ряд 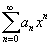 ,
имеющий радиус сходимости R
> 0:
,
имеющий радиус сходимости R
> 0:
![]()
Функция 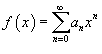 является
непрерывной функцией при |x|
< R.
Степенной ряд внутри интервала сходимости
можно дифференцировать почленно. При
этом производная степенного ряда
выражается формулой
является
непрерывной функцией при |x|
< R.
Степенной ряд внутри интервала сходимости
можно дифференцировать почленно. При
этом производная степенного ряда
выражается формулой
![]()
Степенной ряд можно также почленно интегрировать на отрезке, который расположен внутри интервала сходимости. Следовательно, если − R < b < x < R, то выполняется равенство
![]()
Билет №7
Представление функции в виде
![]() (6.1)
(6.1)
называется ее разложением в степенной ряд.
Теорема 6.1. Если функция f(x) раскладывается в окрестности точки х0 в степенной ряд (6.1) с радиусом сходимости R, то:
функция f имеет на интервале (x0 – R , x0 + R) производные всех порядков, которые можно найти почленным дифференцированием ряда (6.1):
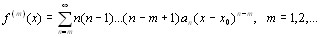 (6.2)
(6.2) 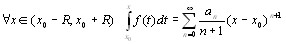 (6.3)
(6.3)ряды (6.1), (6.2) и (6.3) имеют одинаковые радиусы сходимости.
Теорема
6.2. Если функция f раскладывается в
некоторой окрестности точки х0 в
сте-пенной ряд (6.1), то ![]() ,
и, следовательно, справедлива формула
,
и, следовательно, справедлива формула
![]() (6.4)
(6.4)
Доказательство.
Дифференцируя т раз равенство (6.1), получим:
![]()
Примем х = х0 , тогда f(m)(x0) = m!am , что доказывает формулу (6.4).
Определение 6.2. Пусть функция f(x) определена в некоторой окрестности точки х0 и имеет в этой точке производные всех порядков. Тогда ряд
![]()
называется рядом Тейлора.
О: Многочленом Тейлора степени п называется частичная сумма
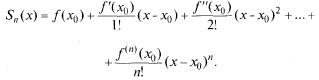
Остаточным членом ряда Тейлора называется
![]() (30.8)
(30.8)
Для
того чтобы бесконечно дифференцируемая
в т.![]() функция
функция![]() являлась
суммой составленного для нее ряда
Тейлора (30.6), необходимо и достаточно,
чтобы
являлась
суммой составленного для нее ряда
Тейлора (30.6), необходимо и достаточно,
чтобы![]()
Используя
определение сходящегося ряда и выражение
(30.8), имеем следующую цепочку: ![]() —
сумма (30.6)
—
сумма (30.6)![]()
![]()
Приведем
запись остаточного члена в форме Лагранжа
![]() (30.9)
где
(30.9)
где![]() находится
между
находится
между![]() и
х.
и
х.
Билет №8
Функция f(x) разлагается в степенной ряд на интервале (-R,R), если на этом интервале данный степенной ряд сходится к функции f(x).
При решении многих задач рекомендуется пользоваться следующими разложениями элементарных функций:
1. ![]() ;
;
2.![]()
![]() ;
;
3. ![]() ,
,
;
4. ![]()
![]() ;
;
5. ![]()
;
6.
|
|
![]() .
.
7. ![]()
Билет №9
Если f(x)
разлагается на отрезке ![]() в
равномерно сходящийся тригонометрический
ряд:
в
равномерно сходящийся тригонометрический
ряд:
![]() (1),(a-нулевое
без деления на 2)
(1),(a-нулевое
без деления на 2)
то это разложение единственное и коэффициенты определяются по формулам:
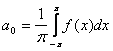 (около
pi
должно быть двойка)
(около
pi
должно быть двойка)
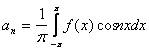
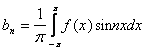 ,
где n=1,2,
...
,
где n=1,2,
...
Тригонометрический
ряд (1) рассмотренного вида с коэффициентами
называется тригонометрическим
рядом Фурье,
а ![]() коэффициентами
ряда Фурье.
коэффициентами
ряда Фурье.
О:
Функция![]() называется
удовлетворяющей условиям Дирихле на
[а, b], если она:
называется
удовлетворяющей условиям Дирихле на
[а, b], если она:
1) непрерывна на [а, b] или имеет конечное число точек разрыва 1 рода;
2) кусочно-монотонна
на [а, b], т.е. отрезок [а, b] можно разделить
на конечное число отрезков, внутри
которых функция![]() либо
только возрастает, либо только убывает,
либо постоянна.
либо
только возрастает, либо только убывает,
либо постоянна.
Пусть
периодическая функция![]() с
периодом
с
периодом![]() удовлетворяет
на любом отрезке из R условиям Дирихле.
Тогда для нее можно найти по формулам
(31.3) коэффициенты
удовлетворяет
на любом отрезке из R условиям Дирихле.
Тогда для нее можно найти по формулам
(31.3) коэффициенты![]() и
построить ряд Фурье
и
построить ряд Фурье
Т
(Дирихле): Если периодическая функция![]() с
периодом
с
периодом![]() удовлетворяет
на любом отрезке из R условиям Дирихле,
то р.Ф. для функции
удовлетворяет
на любом отрезке из R условиям Дирихле,
то р.Ф. для функции![]() сходится
сходится![]() R.
При этом в каждой точке непрерывности
функции
R.
При этом в каждой точке непрерывности
функции![]() сумма
ряда
сумма
ряда![]() а
в каждой точке
а
в каждой точке![]() разрыва
разрыва![]() сумма
сумма![]() .
.
Разложение на (-l; l) выглядит также- только вместо pi в коеффициентах ставится l, а под выражениями синуса и косинуса не nx а pi*nx/l.

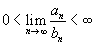 ,
то оба ряда
и
либо
сходятся, либо расходятся;
,
то оба ряда
и
либо
сходятся, либо расходятся;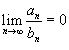 ,
то ряд
сходится,
если сходится ряд
;
,
то ряд
сходится,
если сходится ряд
; ,
то ряд
расходится,
если расходится ряд
.
,
то ряд
расходится,
если расходится ряд
.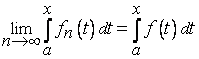 (1)
(1)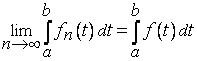 .
(2)
.
(2)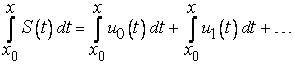 .
(4)
.
(4)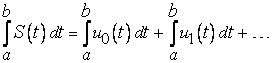 .
(5)
.
(5)