Определение линейной независимости системы векторов

Система векторов A₁, A₂,...,A_n называется линейно независимой, если линейная комбинация этих векторовλ₁*A₁+λ₂*A₂+...+λ_n*A_n равна нулевому вектору только при нулевом наборе чисел λ_1, λ₂,...,λ_n, то есть система уравнений: A₁x₁+A₂x₂+...+A_nx_n =Θ имеет единственное нулевое решение.

2. Базис и координаты. Рассмотрим произвольное вещественное линейное пространство R.  Определение. Совокупность линейно независимых элементов е₁, е₂,..., е_n пространства R называется базисом этого пространства, если для каждого элемента х пространства R найдутся вещественные числа х₁, x₂,..., х_n такие, что справедливо равенство 

х  = x₁e₁ + x₂e₂ + ... + x_ne_n = 0.                                                                             (2.6)

При этом равенство (2.6) называется разложением элемента х по базису е₁, е₂,..., е_n, а числа х₁, x₂,..., х_n  называются координатами элемента х (относительно базиса е₁, е₂,..., е_n).  Докажем, что каждый элемент х линейного пространства R может быть разложен по базису е₁, е₂,..., е_n единственным способом,     т. е. координаты каждого элемента х относительно базиса е₁, е₂,..., е_n определяются однозначно. 

3. Размерность линейного пространства.Как и выше, будем рассматривать произвольное вещественное линейное пространство R.  Определение 1. Линейное пространство R называется n-мерным, если в нем существует п линейно независимых элементов, а любые (n + 1) элементов уже являются линейно зависимыми. При этом число n называется размерностью пространства R.  Размерность пространства R обычно обозначают символом dim R.  Определение 2. Линейное пространство R называется бесконечномерным, если в нем существует любое число линейно независимых элементов.  В настоящей книге мы будем изучать, в основном, пространства конечной размерности п. Бесконечномерные пространства составляют  предмет специального изучения. (Они изучаются в гл. 10 и 11 выпуска «Основы математического анализа», часть П.)  Выясним связь между понятием размерности пространства и введенным в предыдущем пункте понятием базиса.  Теорема 2.5. Если R — линейное пространство размерности n, то любые n линейно независимых элементов этого пространства образуют его базис. 

Определение 1. Подмножество линейного пространства называется подпространством пространства над числовым множеством 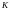, если наряду с двумя произвольными элементами принадлежащими 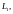ему принадлежит и любая линейная комбинация ( числа).

Например, пространство двумерных геометрических векторов является подпространством трехмерных геометрических векторов В подпространстве существует свой базис, который можно выбрать из базисных векторов пространства .

Введем теперь понятие линейного оператора. Сначала заметим, что любое отображение пространства в пространство ставящее в соответствие каждому элементу единственный элемент по закону называется оператором (действующим из пространства в пространство ).

Билет 26 Определение 2. Оператор называется линейным оператором, если выполняются свойства³:

а) б)

Свойства а) и б) можно объединить в одно:

(при получаем сумму операторов и , при получаем умножение оператора на число). Нетрудно показать, что пространство является линейным пространством.

_{Определение 3.} Матрицей оператора в базисах и называется матрица (размера ), й столбец которой является координатным столбцом образа (образа го базисного вектора пространства ) в базисе

Ниже, если не оговорено противное, будем считать, что все операторы действуют из пространства в себя, т.е. В этом случае матрицу называют матрицей оператора в базисе