Билет 1 Предел функции

дадим понятие предела функции в конечной точке Различают проколотую - окрестность точки которая определяется как симметричный интервал с выброшенной точкой

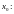
и просто - окрестность точки совпадающую с указанным интервалом:

Пусть функция определена в некоторой проколотой окрестности точки (в самой точке функция можеть быть определена или нет; её значение в точке не существенно).

Определение Говорят, что число P является пределом функции в точке ( или при если для произвольного числа найдется число (зависящее, вообще говоря, от такое, что для всех значений , удовлетворяющих неравенству будет иметь место неравенство При этом пишут

И, наконец, дадим определение предела функции в бесконечности. Сделаем это кратко.

Определение 4. Множества

называются окрестностями точек соответственно. Следующие высказывания являются определениями предела функции в бесконечности:

Перейдем теперь к обоснованию арифметических действий над пределами.

Теорема 5. Если существуют (конечные) пределы то и существуют пределы при этом

Если (кроме существования пределов и ) выполняется ещё условие то существует предел причем

Односторонние пределы

Дадим их кратко. Определение 1. Левый предел функции в точке (обозначение: ): Правый предел функции в точке (обозначение: ): Очевидно следующее свойство:

Для существования обычного предела необходимо и достаточно, чтобы существовали односторонние пределы и чтобы имело место равенство

Билет 2 Бесконечно малые функции

Определение. Функция 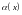называется бесконечно малой функцией в точке или функцией класса , если При этом пишут Таким образом,

Например, функция а функции не являются функциями класса

Следующая теорема устанавливает связь между бесконечно малыми функциями и функциями, имеющими предел при

Теорема 4. Если существует (конечный) предел то Обратно: если функция представляется в виде то имеет предел в точке и

Доказательство. Существование предела 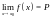эквивалентно высказыванию

Высказывание (4), в свою очередь, эквивалентно тому, что функция т. е. что Теорема доказана.

Замечание 2. Равенство называют асимптотическим разложением функции имеющей предел в точке

Эквивалентные бесконечно малые. Таблица эквивалентных бесконечно малых

Введем следующее понятие. Пусть конечная или бесконечная точка и пусть функ-

ции и определены в некоторой проколотой окрестности точки

Определение 5. Две бесконечно малые функции и (при ) называются

эквивалентными, если в некоторой проколотой окрестности и если

При этом пишут:

Используя эту теорему, а также таблицу эквивалентных бесконечно малых:

Таблица 1.

Если при то при верны следующие соотношения:

const.

можно без особого труда вычислять пределы конкретных функций.

Бесконечно большие функции и их связь с бесконечно малыми

Пусть функция определена в некоторой проколотой окрестности точки

Определение Функция называется бесконечно большой функцией (ББФ) при если для всякого существует число такое, что

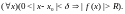При этом пишут

Теорема 7. Пусть функция не обращается в нуль в некоторой проколотой окрестности точки Тогда справедливо высказывание

Иначе говоря, для того чтобы функция была бесконечно малой при необходимо и достаточно, чтобы обратная к ней по величине функция была бесконечно большой при

Теорема Лопиталя Пусть функции и в некоторой проколотой окрестности удовлетворяют требованиям:

и непрерывны и дифференцируемы в

Если при этом существует(конечный или бесконечный) предел отношения производных: то и существует равный ему предел отношения самих функций:

Теорема Лопиталя Пусть функции и в некоторой проколотой окрестности удовлетворяют требованиям:

и непрерывны и дифференцируемы в

Если при этом существует (конечный или бесконечный) предел отношения производных: то и существует равный ему предел отношения самих функций:

Например, для рассмотренного выше предела имеем

Билет 3 Непрерывность функции в точке

Пусть функция определена в точке и некоторой ее окрестности.

Определение Функция называется непрерывной в точке если

т.е. если

Функция называется непрерывной слева (справа) в точке если (соответственно ).

Функция называется непрерывной на множестве если она непрерывна в каждой точке этого множества.

Теорема 1. Пусть сложная функция определена в некоторой проколотой окрестности точки и пусть выполнены условия:

а) существует

б) функция непрерывна в точке

Тогда существует предел и имеет место равенство

Теорема 2. Пусть сложная функция определена в точке и некоторой ее окрестности и пусть выполнены условия:

а) функция непрерывна в точке ,

б) функция непрерывна в соответствующей точке

Тогда сложная функция непрерывна в точке

Теорему 1 называют теоремой о переходе к пределу под знаком непрерывной функции, а теорему 2– теоремой о непрерывности сложной функции

Нетрудно показать, что сумма, разность и произведение двух функций, непрерывных в точке также являются непрерывными в этой точке функциями. Частное двух непрерывных в точке функций непрерывно в этой точке, если

Определение 3.Функции вида

называются простейшими элементарными функциями. Всякая функция, полученная из простейших элементарных функций путем применения к ним конечного числа операций сложения, вычитания, умножения, деления и взятия функций от функций (т.е. образования сложных функций) называется элементарной функцией (общего вида).

Имеет место следующая замечательная теорема.

Теорема 3. Всякая элементарная функция непрерывна в любой внутренней точке своей области определения .

Напомним, что точка называется внутренней точкой множества если она входит в вместе с некоторой своей окрестностью

Если хотя бы одно из условий определения 2 не выполнено, то функция является

разрывной в точке . Различают два типа разрывов:

Точка – точка разрыва I рода: а) существуют и конечные односторонние пределы но либо они не совпадают, либо хотя бы один из них не равен значению ;

б) существуют конечные односторонние пределы но не определена в точке

Точка – точка разрыва II рода: либо не существует хотя бы один из односторонних пределов либо хотя бы один из них равен бесконечности.

Например, точка точка разрыва I рода для функций

а для функции она является точкой разрыва II рода.

Если то прямая 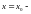вертикальная асимптота для функции Прямая называется наклонной (горизонтальной при ) асимптотой функции , если Нетрудно показать, что если существуют конечные пределы

то прямая асимптота кривой Таким образом, асимптоты функции

могут возникнуть при подходе к точкам разрыва второго рода этой функции либо на бесконечности.

Билет 4 Производная функции в точке, ее геометрический и механический смысл

На рисунке изображены график функции точки секущая, 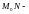касательная к кривой углы Пусть функция определена в точке и некоторой ее окрестности . Сместимся из точки в точку Величина называется приращением аргумента в точке а величина = называется приращением функции в точке (соответствующим приращению аргумента).

Выясним, в чем состоит геометрический смысл производной и дифференциала. Так как и так как то т.е.

т.е. производная функции в точке является угловым коэффициентом касательной к кривой с точкой касания

_{С другой стороны, из рисунка видно,что поэтому}

дифференциал равен приращению касательной к графику функции при переходе аргумента из точки в точку

Из геометрического смысла производной легко получить уравнения касательной и нормали к кривой в точке

(касательная), (нормаль).

Выясним теперь механический смысл производной. Если 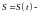путь пройденный материальной точкой за время от момента до момента то средняя скорость материальной точки, а величина

мгновенная скорость материальной точки в момент

Билет 5 Теорема 1. Пусть сложная функция определена в некоторой проколотой окрестности точки и пусть выполнены условия:

а) существует

б) функция непрерывна в точке

Тогда существует предел и имеет место равенство

Теорему 1 называют теоремой о переходе к пределу под знаком непрерывной функции,

Производная сложной функции

Теорема 5. Пусть сложная функция определена в точке и некоторой ее окрестност и пусть выполнены условия:

1. функция дифференцируема в точке

2. функция дифференцируема в соответствующей точке

Тогда сложная функция дифференцирума в точке и имеет место равенство

Логарифмическая производная

При дифференцировании показательно-степенной функции обычно используют логарифмическую производную Делается это так:

Например,

Билет 6 Понятие дифференциала функции, его геометрический смысл. Дифференциалом функции   в   называется главная, линейная относительно  , часть приращения функции.

.

Покажем, что   и   эквивалентные бесконечно малые при  :

(  - бесконечно малая).

Геометрический смысл дифференциала:

Пр оведем к графику функции   в точку   касательную   и рассмотрим ординату этой касательной для точки  . На рисунке ,  . Из прямоугольного треугольника   имеем:  , т.е.  . Но, согласно геометрическому смыслу производной,  . Поэтому   или  . Это означает, что дифференциал функции   в   равен приращению ординаты касательной к графику функции в этой точке, когда   получает приращение  .

Теорема 4. Если функции дифференцируемы в точке то в этой точке дифференцируемы и функции причем

(в рассматриваемой точке ).

Если, кроме того, то в точке дифференцируемо и частное, причем

Доказательство проведем для производной суммы. Имеем поэтому

Теорема доказана.

Таблица производных

1)

2)

3)

4)

5)

6)

7)

Билет 7 Производные и дифференциалы высших порядков

Производная есть сама функция от поэтому можно взять от нее производную. Полученная таким образом функция (если она существует) называется второй производной от функции и обозначается И вообще:

если известна производная ( порядка), то производная го порядка определяется так: При этом функция называется раз дифференцируемой в точке

Аналогично определяются дифференциалы высшего порядка. Именно:

если известен дифференциал порядка то дифференциал го порядка определяется так: при этом дифференциал независимой переменной и все его степени считаются постоянными дифференцирования.

Имеем И вообще, справедливо утверждение: если функция дифференцируема раз в точке то

Формула Лейбница. Если функции дифференцируемы раз в точке то имеет место равенство

Билет 8 Формула Тейлора с остаточными членами в форме Пеано и Лагранжа

При вычислении пределов функций мы использовали таблицу 1 эквивалентных бесконечно малых. Например, при вычислении предела мы использовали формулы Однако этих формул не достаточно для вычисления предела

Нужны более точные формулы или так называемые асимптотические разложения высших порядков. Переходя к описанию таких разложений, введем следующее понятие.

Определение 5. Пусть функция определена в некоторой проколотой окрестности

точки Говорят, что функция имеет в точке асимптотическое разложение го порядка, если существуют числа такие, что в некоторой в некоторой проколотой окрестности представляется в виде

Здесь Равенство (3) означает, что функция аппроксимируется (приближенно равна) в некоторой малой окрестности точки многочленом. В каком случае функция имеет асимптотическое разложение порядка? Ответ на этот вопрос содержится в следующем утверждении.

Теорема 2. Пусть функция имеет в точке производные до го порядка включительно. Тогда имеет в точке асимптотическое разложение порядка вида

(формулу (4) называют формулой Тейлора с остаточным членом в форме Пеано или локальной формулой Тейлора).

Теорема 4. Пусть функция удовлетворяет следующим условиям:

1) существуют и непрерывны на отрезке ;

2) производная существует и конечна по-крайней мере на интервале

Тогда для всех функция представляется в виде

где точка находится между и

Формулу (5) называют (глобальной) формулой Тейлора с остаточным членом в форме Лагранжа.

Применения формулы Тейлора

а) Приближенное вычисление значений функции. Если в формуле (4) (или (5)) отбросить остаточный член, то получим приближенное значение функции

с точностью до модуля остаточного члена. Если величина то и погрешность этого приближенного равенства будет очень малой. Например, При этом

Билет 9 Монотонность функции

Напомним определение монотонных функций.

Определение 1. Говорят, что функция строго возрастает на множестве если для любых из неравенства вытекает неравенство Если же то функция называется строго убывающей на множестве Если же из строгого неравенства между аргументами вытекают нестрогое неравенство между значениями функции, то говорят, что является неубывающей (соответственно невозрастающей ) на множестве Множество всех функций строго возрастающих и строго убывающих образует класс строго монотонных функций; невозрастающие и неубывающие функции образует класс просто монотонных функций.

При исследовании на монотонность функций используются выписанная ранее

Теорема Лагранжа. Если функция непрерывна на отрезке и является дифференцируемой по-крайней мере в интервале то существует точка такая, что

Теорема 1. Пусть функция непрерывна на отрезке и является дифференцируемой по-крайней мере в интервале Тогда справедливы следующие высказывания:

1. если то функция строго возрастает на отрезке ;

2. если то функция строго убывает на отрезке .

Доказательство вытекает из равенства (1), в котором надо положить Действительно, если а (тогда и ), то (см. (1)) будет

выполняться неравенство 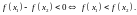Это означает, что функция строго возрастает на отрезке . Аналогично доказывается высказывание 2. Теорема доказана.

Локальный экстремум

Пусть функция определена в точке и некоторой её окрестности.

Определение 2. Говорят, что функция достигает в точке локального максимума, если существует такое, что выполняется неравенство . Если при указанных имеет место противоположное неравенство то говорят, что в точке функция достигает в точке локального минимума.

Заметим, если неравенства или обращаются в равенство лишь в одной точке то говорят, что соответствующий максимум или минимум является строгим. Точки функция достигает локального максимума или минимума, называются точками локального экстремума этой функции.

Замечание 2. Слово “локальный” здесь означает, что введенное понятие экстремума верно лишь в достаточно малой окрестности точки Иногда слово “локальный” будем опускать.

Необходимое условие экстремума. Пусть в точке функция достигает локального экстремума. Тогда либо в этой точке функция дифференцируема и тогда либо не дифференцируема в точке

Замечание 3. Точки такие, что либо равна нулю, либо не существует (или равна ), называтся критическими точками функции

Теорема 2 (достаточные условия экстремума по первой производной). Пусть точка критическая точка для функции и функция непрерывна в этой точке. Пусть, кроме того, производная существует в некоторой проколотой окрестности точки Тогда:

1. если при переходе аргумента через точку (слева направо) изменяет знак с на то в точке функция достигает локального максимума;

2. если при переходе аргумента через точку (слева направо) изменяет знак с на то в точке функция достигает локального минимума;

3. если в окрестности точки функция не изменяет знака, то в точке функция не достигает локального экстремума.

Выпуклость, вогнутость, точки перегиба

Пусть функция дифференцируема в точке Тогда в точке она имеет касательную, каждая точка которой удовлетворяет уравнению

Определение 3. Говорят, что кривая выпукла вверх в точке если существует такое, что в окрестности кривая находится

ниже своей касательной (3) в точке т.е. если Если же

то кривая называется выпуклой вниз в точке (часто говорят, о выпуклости или вогнутости в точке ). Говорят, что кривая выпукла вверх (выпукла вниз) на интервале если она выпукла вверх (выпукла вниз) в каждой точке этого интервала.

На рисунке Р.2 функция выпукла вверх в точке а на Р.3 – выпукла вниз.

Теорема 3. Пусть функция дважды дифференцируема на интервале . Тогда справедливы высказывания:

1. если то кривая выпукла вверх на

2. если то кривая выпукла вниз на

Определение 4. Точка называется точкой перегиба кривой если:а) дифференцируема в точке ; б) кривая при переходе через точку изменяет направление выпуклости (это равносильно тому, что разность изменяет знак при переходе через точку ).

Необходимое условие точки перегиба. Если - точка перегиба и если существут то

Доказательство вытекает из локальной формулы Тейлора и из равенства

Замечание 4. К точкам, подозрительным на “перегиб”, следует отнести, прежде всего, точки , для которых Однако “перегиб” может иметь место и в точках, в которых вторая производная не существует или равна Например, в точке функция имеет производную И в этой точке эта функция имеет “перегиб”. Очевиден следующий результат.

Теорема 4 (достаточное условие точки перегиба). Пусть функция дифференцируема в точке и некоторой её окрестности и дважды дифференцируема в некоторой проколотой окрестности этой точки. Тогда если при переходе через точку вторая производная изменяет знак, то точка перегиба кривой

Билет 10 Свойства функций, непрерывных на отрезке

Функция называется непрерывной на отрезке если а) она непрерывна в любой точке 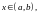а на концах и отрезка непрерывна справа и слева соответственно, т.е. Функции, непрерывные на отрезке, обладают рядом замечательных свойств, сформулированных ниже.

1. Теорема Вейерштрасса Если функция непрерывна на отрезке то она ограничена на этом отрезке, т.е. существует постоянная такая, что

2. Теорема Вейерштрасса Если функция непрерывна на отрезке то она достигает на этом отрезке своих наибольшего и наименьшего значений, т.е. существуют точки такие, что

3. Теорема Больцано-Коши Если функция непрерывна на отрезке то каково бы ни было значение существует значение такое, что

4. Теорема Больцано-Коши Если функция непрерывна на отрезке и принимает на концах этого отрезка значения разных знаков то существует хотя бы одно значение такое, что

    Теорема 5.2 (Ролля)   Пусть функция   дифференцируема на интервале  , непрерывна в точках   и   и принимает в этих точках значение 0:  . Тогда найдётся хотя бы одна точка  , в которой  .

        Замечание 5.2   Это утверждение можно переформулировать так: между двумя корнями   и   дифференцируемой функции   обязательно найдётся корень её производной   (то есть точка  , такая что  ). Условие   означает, что касательная, проведённая к графику   при  , расположена горизонтально.

Заметим также, что теорема Ролля не утверждает, что корень   -- единственный корень производной на интервале  ; на этом интервале может находиться несколько корней производной.     

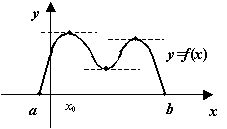
Рис.5.4.Между двумя корнями дифференцируемой функции лежит хотя бы один корень её производной

        Теорема 5.3 (Лагранжа)   Пусть функция   дифференцируема на интервале   и непрерывна в точках   и  . Тогда найдётся такая точка  , что

(5.1)

        Замечание 5.3   Формулу (5.1) можно записать в виде

(5.2)

Если считать, что аргументу   придано приращение  , то функция получает приращение  . (При этом мы не считаем, что   и   стремятся к 0, то есть это конечные, а не бесконечно малые, приращения.) При этих обозначениях формулу (5.2) мы можем записать в виде

в котором участвуют конечные приращения аргумента и функции. Поэтому формулу (5.2) называют формулой конечных приращений.     

           Теорема 5.4 (Коши)   Пусть функции   и   дифференцируемы на интервале   и непрерывны при   и  , причём   при всех  . Тогда в интервале   найдётся такая точка  , что

        

Билет 11 Операция, обратная дифференцированию, называется интегрированием. Перейдем к ее изложению.

Первообразная и неопределенный интеграл

Ниже в качестве берется любой из промежутков: (концы и могут быть бесконечными).

Определение 1. Говорят, что функция является первообразной для функции на множестве если Разыскание всех первообразных функции называется интегрированием

Например, функция является первообразной для на всей оси так как

Теорема 1(об общем виде всех первообразных данной функции). Пусть фиксированная первообразная функции (на множестве ). Тогда множество всех первообразных функции (на множестве ) описывается формулой

где произвольная постоянная.

Доказательство вытекает из того, что если и две первообразные функции , то а, значит, разность является постоянной величиной на множестве , т.е.

Определение 2. Совокупность всех первообразных функции (на множестве ) называется неопределенным интегралом на этой функции. Обозначение: При этом сама функция называется подынтегральной функцией и если интеграл от нее существует, то говорят, что интегрируема на .

Таблица неопределенных интегралов (ниже везде произвольная постоянная)

Замена переменной в неопределенном интеграле

Перейдем к формулировке теоремы о замене переменной в неопределенном интеграле, которая часто используется при вычислении интегралов. Здесь имеются в виду два утверждения¹:

где функция, обратная к функции

Теорема 2. а) Пусть выполнены условия: 1) функция непрерывна в своей области определения б) функция непрерывно дифференцируема на множестве таком, что

Тогда для всех имеет место равенство

б) Пусть выполнены условия: 1) функция непрерывна в своей области определения

2) функции и непрерывны на множестве таком, что

3) 4) функция имеет на множестве обратную функцию Тогда для всех имеет место равенство

Замечание 1. Преобразования в часто называют процедурой введения множителя под знак дифференциала. Формулу удобно применять в тех случаях, когда функция легче интегрируется, чем исходная функция Её применяют, например, при вычислении интегралов от иррациональностей вида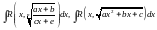 (здесь рациональная функция). В первом случае делается замена во втором случае подбирают такую замену чтобы исчезла иррациональность.

Например,

= Далее надо вернуться к старой переменной с помощью обратной функции и получить ответ:

Интегрирования по частям в неопределенном интеграле

При вычислении интегралов часто используется операция интегрирования по частям, законность которой регламентируется следующим утверждением.

Теорема 3. Пусть функции непрерывно дифференцируемы на множестве Тогда на этом множестве справедливо равенство

Доказательство вытекает из цепочки тождеств

Замечание 2. Операция интегрирования по частям применяется к интегралам вида

( многочлен степени ).

При этом в интегралах типа 1 для получения дифференциала надо ввести под знак дифференциала трансцендентную функцию а в интегралах типа 2 под знак дифференциала надо ввести многочлен Например,

Билет 12 Определенный интеграл, его свойства и геометрический смысл

П усть функция определена на отрезке Произведем разбиение (см. Р5)

отрезка на частичные отрезки и выберем произвольно точки Вычислим значения

и составим так называемую интегральную сумму

Определение 3. Если существует конечный предел интегральных сумм:

и если этот предел не зависит от вида разбиения и выбора точек то его называют определенным интегралом от функции на отрезке Обозначение: При этом саму функцию называют интегрируемой на отрезке

Мы пришли к следующему геометрическому смыслу определенного интеграла:

интеграл численно равен площади криволинейной трапеции с верхней границей, описываемой уравнением

Замечание 3. В определении 3 интеграла предполагается, что отрезок интегрирования ориентирован от до (т.е. ). В случае противоположной ориентации отрезка (т.е. при ) полагаем по определению Также полагаем по определению, что

Линейность интеграла. Если функции и интегрируемы на отрезке то на этом отрезке интегрируема и любая их линейная комбинация и имеет место равенство

Аддитивность интеграла. Если функция интегрируема на максимальном из отрезков то она интегрируема и на двух других отрезках, причем имеет место равенство

Далее везде предполагаем, что

Монотонность интеграла. Если функции и интегрируемы на отрезке и то

Интегрируемость модуля. Если функции интегрируема на отрезке то на этом отрезке интегрируема и функция причем имеет место неравенство

Теорема о среднем для интеграла. Пусть функция непрерывна на отрезке Тогда существует точка 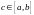такая, что (геометрический смысл этой теоремы состоит в том, что существует прямоугольник с основанием и высоты равновеликий криволинейной трапеции ).

Доказательство. Пусть (по теореме Вейерштрасса значения и функцией достигаются). Имеем поэтому из свойства монотонности интеграла отсюда получаем

Последние неравенства показывают, что значение является промежуточным для функции на отрезке а, значит, по теореме Больцано-Коши существует такое, что

Теорема доказана.

Билет 13 Интеграл с переменным верхним пределом

Заметим, что в качестве переменной интегрирования можно выбрать любую букву:

Пусть функция интегрируема на отрезке Тогда для любого можно вычислить число Значит, для каждого определена функция Эту функцию называют интегралом с переменным верхним пределом.

Теорема 1. Если функция интегрируема на отрезке то интеграл непрерывен на этом отрезке. Если непрерывна на отрезке то

дифференцируема на указанном отрезке, причем

Доказательство первой части этого утверждения опускаем. Перейдем к обоснованию второй части. Пусть произвольная точка интервала Вычислим

Так как непрерывна на отрезке то применима теорема о среднем: существует точка такая, что

Тогда Устремляя здесь и учитывая, что при этом т.е. Равенство (1) показано в любой внутренней точке отрезка Можно показать, что оно верно и на концах этого отрезка. Теорема доказана.

Следствие 1. Любая непрерывная на отрезке функция имеет первообразную.

Действительно, в качестве одной из первообразных можно указать интеграл с переменным верхним пределом ( ).