Фазовая скорость.

Найдем выражение для скорости v продольной волны в однородной газообразной среде.

О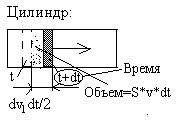 тносительная деформация выделенного объема при возмущающем действии поршня за время dt:

, где S – площадь поршня.

Добавочное давление dp можно найти из з-на Гука (где dV/V=d):

Под действием силы dF=S dp возмущенный поршнем газ приобретает импульс, равный ,  - плотность газа. По II-му закону Ньютона

, откуда искомая скорость волны:

Замечание. Предполагается, что =const.

Групповая скорость.

Основываясь на принципе суперпозиции, можно заменить любую несинусоидальную волну эквивалентной ей системой синусоидальных волн, т.е. представить ее в виде волнового пакета.

За скорость распространения такой несинусоидальной волны принимают скорость u перемещения точки М, в которой амплитуда имеет какое-нибудь фиксированное значение. Следовательно, точка М движется по закону , откуда

Найдем

Связь между групповой и фазовой скоростью:

Так как , то

Квантовая оптика.

Фотон.

- это элементарная частица. Определим характеристики фотона как частицы.

Энергия

Импульс, масса

, (т.к. v=c) – такого быть не может, поэтому говорят, что фотон имеет массу покоя , т.е. по этой формуле массу фотона находить нельзя.

, если , то

- это определение импульса фотона.

- волновое число

Квантово-волновой дуализм.

Волны	Кванты
Свет может проявлять себя как в волновых, так и в квантовых опытах.
1. Интерференция	1. Внешний фотоэффект
2. Дифракция	2. Эффект Комптона.
3. ,k,	3. Энергия, импульс: ,p,c

Внешний фотоэффект.

Эффект вырывания электронов с поверхности вещества в результате действия квантов света.

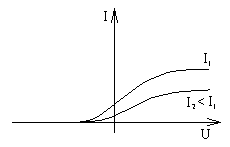
Вольт-амперная характеристика вакуумного фотодиода с фотокатодом.

Лучший нейтральный светофильтр - сетка. Если изменится частота, то фотоэффект может пропасть совсем.

Свойства фотоэффекта:

1. Фотоэффект безынерционен.

2. Ток насыщения

3. Существует красная граница фотоэффекта

Уравнение Эйнштейна для внешнего фотоэффекта.

получаем из условия

Эффект Комптона.

В этом эффекте проявляются квантовые свойства света.

У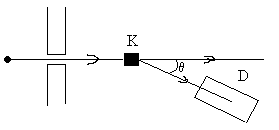 зкий пучок монохроматического рентгеновского излучения радает на «легкое» рассеивающее вещество К, и после рассеяния на угол  измеряется длина рассеянного излучения. Опыты Комптона показали, что длина волны рассеянного излучения больше длины волны падающего излучения:

, причем  зависит только от угла .

С квантовой точки зрения рассеяние – результат взаимодействия фотонов падающего излучения с электронами вещества.

Фотон:

- импульс

Электрон:

Происходит рассеяние фотона на электроне. Фотон получает импульс и энергию ; электрон приобретает импульс и энергию

- закон сохранения энергии

- закон сохранения импульса.

Подробнее:

,

откуда (учитывая что )

Т.к.

Из этой формулы видно, что ' =  в двух случаях:

1) =0 (рассеяние отсутствует)

2) Падающее излучение имеет очень малую частоту, при которой . (В этом случае знаменатель стремится к еденице)

Заменяя  по формуле и подставляя в выражение для  получим: