Определение оптимального плана

Число занятых клеток равно (m+n-1)=5+3-1=7, план является не вырожденным, потенциалы и могут быть рассчитаны.

Если бы число занятых клеток было меньше, чем (m+n-1), то не хватило бы количество уровней для определения потенциалов. Для этого носят нуль в одну из свободных клеток таблицы так, чтобы общее число занятых клеток стало равным (m+n-1). Нуль вводят в клетку с наименьшим тарифом, чтобы в каждой строке и каждом столбце было не меньше одной занятой клетки.

Найденное исходное опорное решение проверяется на оптимальность методом потенциалов по следующему критерию: если опорное решение транспортной задачи является оптимальным, то ему соответствует система действительных чисел и , удовлетворяющих условиям для занятых клеток и для свободных клеток.

Проверим найденное опорное решение на оптимальность, добавив в распределительную таблицу столбец и строку .

Полагая , запишем это значение в последнем столбце таблицы.

Рассмотрим занятую клетку первой строки, которая расположена в первом столбце (1,1), для нее выполняется условие , откуда . Т.к. , то . Это значение запишем в последней строке таблицы. Далее надо рассматривать ту из занятых клеток таблицы, для которой один из потенциалов известен. Рассмотрим занятую клетку (1,5): 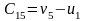, откуда . Т.к. , то .

Таблица 3

	240	480	120	320	160
360	7 200	10	13	9	0 160	0
440	14	9 440	12	10	0	0
520	10 40	12 40	9 120	7 320	0	-3
	7	9	6	4	0

Для клетки (2, 2):

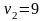
Для клетки (3, 1): , ,

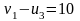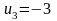
Для клетки (3, 2): , ,

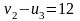Для клетки (3, 3): , ,

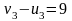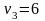Для клетки (3, 4): , ,

Найденные значения потенциалов заносим в таблицу. Вычисляем оценки свободных клеток:

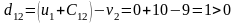
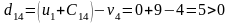
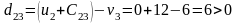
Все (отрицательных оценок нет ) значит, опорное решение является оптимальным.

Х_опт = .

Стоимость транспортных расходов составит:

f (X_опт) = 200 · 7 + 440 ·9 + 40 · 10 + 120 · 9 + 320 · 7 +12·40= 9360.

По оптимальному плану Х_опт следует перевезти от поставщика А₁ потребителям В₁ продукцию в количестве 200 единиц соответственно, от поставщика А₂ потребителю В₂ - 440 единиц, от поставщика А₃ - потребителям В₁, В₂, В₃ и В₄ – 40,40, 120 и 320 единиц соответственно.

При этом суммарные затраты на перевозку продукции от поставщиков к потребителям будут минимальными и составят f_min = 9360 денежных единиц.

У поставщика А₁ останется невостребованными 160 единиц продукции.

Задача 3.

Предприятие потребляет некоторый ресурс X (един.в месяц) и выпускает продукцию, которую продает и получает доход Y (денежных един. в месяц).

Этот процесс продолжается в течении 10 месяцев. Значения X и Y приведены в таблице 3. Необходимо построить линейную модель зависимости Y от X методом наименьших квадратов. Решение проиллюстрировать графически. Сделать выводы экономического характера с использованием полученной модели.

Таблица 3

Вариант	1
Переменные	Х	Y
1	2	4
2	6	5
3	16	12
4	12	3
5	8	10
6	4	5
7	20	16
8	17	14
9	7	9
10	11	15