Решение
Исходя из условия задачи имеем:
А =
;
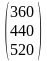с = (2 3 5); В = (240 480 120 320); С =
.
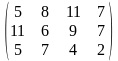Построение экономико-математической модели
Запишем начальные условия задачи в форме табл. 1.
Таблица 1
Поставщики |
Мощности поставщиков |
Себестоимость продукции |
Пункты потребления и их спрос |
|||
В1 |
В2 |
В3 |
В4 |
|||
240 |
480 |
120 |
320 |
|||
А1 |
360 |
2 |
5+2=7 x11 |
8+2=10 x12 |
11+2=13 x13 |
7+2=9 x14 |
А2 |
440 |
3 |
11+3=14 x21 |
6+3=9
x22 |
9+3=12
x23 |
7+3=10
x24 |
А3 |
520 |
5 |
5+5=10 x31 |
7+5=12 x32 |
4+5=9 x33 |
2+5=7 x34 |
Обозначим через
xij (i =
;
j =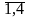
)
количество продукции, которое планируется
перевезти от поставщика Ai потребителю
Bj, а через f - суммарные затраты на
производство и перевозку.
Непосредственно в таблице подсчитываем суммарные тарифы на производство и перевозку продукции из пункта Ai (i = ) в пункт Bj (j = ).
Целевая функция задачи запишется в виде:
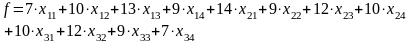(1)
Запишем ограничения, накладываемые мощностями поставщиков:
x11 + x12 + x13 + x14 360;
x21 + x22 + x23 + x24 440; (2)
x31 + x32 + x33 + x34 520.
Спрос пунктов потребления выражаем в виде равенств:
x11 + x21 + x31 = 240;
x12 + x22 + x32 = 480; (3)
x13 + x23 + x33 = 120;
x14 + x24 + x34 = 320.
Если исключить обратные перевозки, должны выполняться ограничения:
xij 0 (i = ; j = ). (4)
Соотношения (1) - (4) образуют экономико-математическую модель рассматриваемой задачи: целевая функция (1), описывающая транспортные затраты, минимизируется при ограничениях (2) - (4).
Сравнивая суммарную мощность поставщиков 360 + 440 + 520 =1320 с суммарным спросом пунктов потребления 240 + 480 + 120 + 320 = 1160, видим, что эти суммы не совпадают. Имеем открытую транспортную задачу.
Часть произведенной поставщиками продукции (1320 - 1160 = 160 единиц) останется нераспределенной. Введем в рассмотрение фиктивного потребителя В5 со спросом, равным небалансу, т.е. 160 единицам, с одинаковыми затратами на перевозку, равными ci5 = 0 (i = ). Пятый столбец будем рассматривать в последнюю очередь.
Построение исходного опорного плана
Построим опорный план по правилу минимального элемента.
В клетку (1; 5) с тарифом 0 впишем число х15 = 160, удовлетворив спрос потребителя В5 - пятый столбец исключаем из рассмотрения.
В клетку (3; 4) с тарифом 7 впишем число х34 = 320, удовлетворив спрос потребителя В4 - четвертый столбец исключаем из рассмотрения.
В клетку (1; 1) с тарифом 7 впишем число х11 = 200, исчерпав запасы поставщика А1 - первую строку исключаем из рассмотрения.
В клетку (3; 3) с тарифом 9 впишем число х33 = 120, удовлетворив спрос потребителя В3 - третий столбец исключаем из рассмотрения.
В клетку (2; 2) с тарифом 9 впишем число х22 = 440, удовлетворив спрос потребителя А2 - вторую строку исключаем из рассмотрения.
В клетку (3; 1) с тарифом 10 впишем число х31 = 40, удовлетворив спрос потребителя В1 - первый столбец исключаем из рассмотрения.
В клетку (3; 2) с тарифом 12 впишем число х32 = 40, удовлетворив спрос потребителя В2 - второй столбец исключаем из рассмотрения.
Оставшуюся у поставщика А3 продукцию в объеме 160 единиц распределяем фиктивному потребителю В5. Окончательно получаем табл. 2.
Таблица 2
|
240 |
480 |
120 |
320 |
160 |
360 |
7
200 |
10
|
13 |
9
|
0 160 |
440 |
14 |
9 440
|
12 |
10 |
0 |
520 |
10 40 |
12 40 |
9 120
|
7 320 |
0
|
Исходным опорным планом перевозок является
Х1
=
.
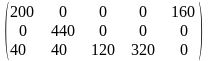Этому плану соответствует значение целевой функции:
f (X1) = 200 · 7 + 440 ·9 + 40 · 10 + 120 · 9 + 320 · 7 +12·40= 9360
(без учета показателей фиктивного потребителя).