Равновесие тела при наличии трения качения

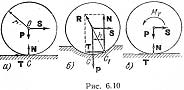
Рассмотрим цилиндр (каток), покоящийся на горизонтальной плоскости, когда на него действует горизонтальная активная сила S; кроме нее, действуют сила тяжести Р, а также нормальная реакция N и сила трения Т (рис. 6.10, а). При достаточно малом модуле силы S цилиндр остается в покое. Но этот факт нельзя объяснить, если удовлетвориться введением сил, изображенных на рис. 6.10, а. Согласно этой схеме равновесие невозможно, так как главный момент всех сил, действующих на цилиндр МСz= –Sr, отличен от нуля, и одно из условий равновесия не выпол­няется. Причина этого несоответствия состоит в том, что мы представляем это тело абсолютно твердым и предполагаем касание цилиндра с по­верхностью происходящим по образующей. Для устранения отмечен­ного несоответствия теории с опытом необходимо отказаться от гипотезы абсолютно твердого тела и учесть, что в действительности цилиндр и плоскость вблизи точки С деформируются и существует некоторая площадь соприкосновения конечной ширины. Вследствие этого в ее правой части цилиндр прижимается сильнее, чем в левой, и полная реакция R приложена правее точки С (см. точку С1 на рис. 6.10, б). Полученная схема действующих сил статически удовле­творительна, так как момент пары (S,Т) может уравновеситься мо­ментом пары (N,Р). В отличие от первой схемы (рис. 6.10, а), к цилиндру приложена пара сил с моментом МT=Nh.(6.11). Этот  момент называется  моментом  трения качения. h=Sr/, где h-расстояние от C до C1. (6.13). С увеличением модуля активной силы S растет расстоя­ние h. Но это расстояние связано с площадью поверхности контакта и, следовательно, не может неограниченно увеличиваться. Это зна­чит, что наступит такое состояние, когда увеличение силы S при­ведет к нарушению равновесия. Обозначим максимально возможную величину h буквой d. Величина d пропорциональна радиусу цилиндра и различна для разных материалов. Следовательно, если имеет место равновесие, то выполняется условие: h<=d.(6.14). d называется коэффициентом трения качения; она имеет размерность длины. Условие (6.14) можно также записать в виде Мт<=dN, или, учитывая (6.12), S<=(d/r)N.(6.15).  Очевидно, что максимальный момент трения качения MTmax=dN  пропорционален  силе  нормального давления.

 

Коэффициент трения устанавливает пропорциональность между силой трения и силой нормального давления, прижимающей тело к опоре. Коэффициент трения является совокупной характеристикой пары материалов которые соприкасаются и не зависит от площади соприкосновения тел.

Виды трения

Трение покоя проявляется в том случае, если тело находившееся в состоянии покоя, приводится в движение. Коэффициент трения покоя обозначается μ0.

Трение скольжения проявляется при наличии движения тела, и оно значительно меньше трения покоя.

1.

μск < μ0

Трение качения проявляется в том случае, когда тело катится по опоре, и оно значительно меньше трения скольжения.

2.	μкач << μск

Сила трения качения зависит от радиуса катящегося предмета. В типичных случаях (при расчетах трения качения колес поезда или автомобиля), когда радиус колеса известен и постоянен, его учитывают непосредственно в коэффициенте трения качения μкач.

Определение коэффициента трения

К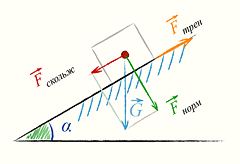 оэффициент трения можно определить экспериментально. Для этого помещают тело на наклонную плоскость, и определяют угол наклона при котором:

коэффициент трения покоя

тело начинает двигаться (коэффициент трения покоя μ0)

коэффициент трения скольжения

тело движется с постоянной скоростью (коэффициент трения скольжения μ).

3.	μFн= Fс
4.	μGcos(α)= Gsin(α)

5.

μ=tg(α)

Здесь: μ — искомый коэффициент трения, α — угол наклона плоскости

Коэффициенты трения качения.

Сила трения качения описывается как:

F_тр=k_тр(F_n/r) , где k_тр- коэффициент трения а F_n - прижимающая сила, а r - радиус колеса.

Размерность коэффициента трения качения, естественно, [длина].

Коэффициенты трения скольжения.

Сила трения скольжения описывается как:

F_тр=k_трF_n , где k_тр- коэффициент трения а F_n - прижимающая сила .