Сила. Система сил. Равновесие абсолютно твердого тела.

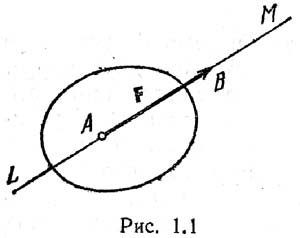
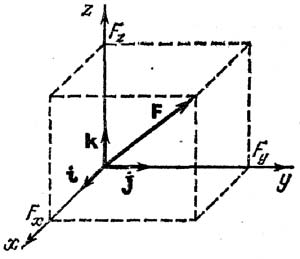
В механике под силой понимается мера механического взаимодействия материальных тел, в результате которого взаимо­действующие тела могут сообщать друг другу ускорения или де­формироваться (изменять свою форму). Сила— векторной величиной. Она характеризуется чис­ленным значением, или модулем, точкой приложения и направлением. Точка приложения силы и ее направление определяют линию действия силы. На рисунке показано, как сила приложена к точке A. Отрезок AB= модулю силы F. Прямая LM называется линией действия силы. В сист. СИ сила изм. в ньютонах (Н). Так же есть 1МН=10⁶Н, 1 кН=10³Н. Существует 2 способа задания силы: непосредственным описанием и векторный (ч-з проекции на оси координат). F= F_xi + F_yj + F_zk , где F_x, F_y, F_z– проекции силы на оси координат, а i, j, k - единичные орты. Абсолютно твёрдое тело— тело в котором расстояние м-ду 2 его точками ост. неизменным независимо от действия на него сил.

Совокупность нескольких сил (F₁, F₂, ... ,F_n) называется системой сил. Если, не нарушая состояния тела, одну систему сил (F₁, F₂, ..., F_n) можно заменить другой си­стемой (Р₁, P ₂ , ... , P_n) и наоборот, то такие системы сил называются эквивалентными. Символически это обозначается следую­щим образом: ( F ₁ , F ₂ , ... , F_n )~ (Р₁, P ₂ , ... , P_n). Однако, это не означает, что если две системы сил оказывают одинаковое действие на тело они будут эквивалентны. Эквивалентные системы вызывают одинаковое состояние системы. Когда система сил ( F ₁ , F ₂ , ... , F_n ) эквивалентна одной силе R, то R назыв. равнодействующей. Равнодействующая сила может заменить действие всех данных сил. Но не всякая си­стема сил имеет равнодействующую. В инерциальной системе координат выпол­няется закон инерции. Это означает, в частности, что тело, находя­щееся в начальный момент в покое, останется пребывать в этом состо­янии, если на него не действуют никакие силы. Если абсо­лютно твердое тело остается в состоянии покоя при действии на него  системы  сил   ( F ₁ , F ₂ , ... , F_n ),   то эта система называется   уравно­вешенной, или системой сил, эквивалентной нулю: ( F₁ , F ₂ , ... , F_n )~0. В этом случае говорят, что тело находится в равновесии. В математике два вектора считаются равными, если они параллельны, направлены в одну сторону и равны по модулю. Для эквивалентности двух сил этого недостаточно и из равенства F=Р еще не следует соотношение F~Р. Две силы эквива­лентны, если они векторно равны и приложены к одной точке тела. 

Аксиома 3 (закон параллелограмма). Равнодействующая двух сил, приложенных к одной точке тела под углом друг к другу, выражается по величине и по направлению диагональю параллелограмма, построен­ного на заданных силах (рис.1.6):

 

 .

 

 Величину равнодействующей силы можно определить по теореме косинусов

 

 

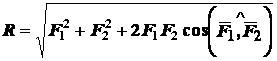
или по теореме синусов

 

 .

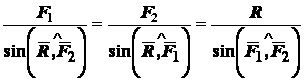 Аксиома 4 (о действии и противодей­ствии). Два тела дейст­вуют друг на друга с силами, равными по величине и направлен­ными по одной прямой в противопо­ложные стороны (рис. 1.7).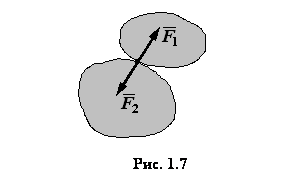

 Заметим, что эти силы приложены к разным телам.

Принцип отвердения.

Деформируемое твердое тело может рассматриваться как изменяемая система материальных точек. Поэтому те аксиомы статики, которые относятся к изменяемой системе, сохраняются в сопротивлении материалов. В частности, к деформируемому твердому телу применима аксиома отвердения, которую формулируют так: равновесие системы не нарушается от наложения лишних связей. Мысленно превращая деформируемое тело в абсолютно твердое, мы налагаем на него лишние связи. Значит, равновесие деформируемого тела не нарушается, если его превратить в абсолютно твердое. После этого для него можно составлять уравнения статики твердого тела, которые, таким образом, сохраняют силу и в сопротивлении материалов.

При применении принципа (аксиомы) отвердения необходимо предположить, что сначала тело получает деформацию, а потом, для определения реакций связей, его можно превращать в абсолютно твердое.

Рассмотрим, например, балку (рис. 2), лежащую на трех опорах и нагруженную двумя сосредоточенными силами (термин «сосредоточенная сила» нужно понимать в том смысле, как это разъяснено выше).

Если считать балку абсолютно твердой, то вопрос об определении реакций лишен смысла. В действительности под действием сил балка прогнется, как указано на рис. 2 пунктиром. Только после изгиба в опорах возникнут совершенно определенные реакции.

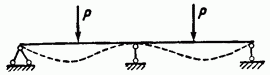
Рис. 2.

Представим себе, что после деформации балка стала абсолютно жесткой. Величины реакции от этого не изменились, но мы получаем право составлять уравнения равновесия обычным способом. Конечно, в данном случае этих уравнений недостаточно для нахождения реакций.

Из принципа отвердения вытекают два свойства фундаментальной важности:

1) реакции связей в статически неопределимых системах удовлетворяют уравнениям статики, составленным так, как если бы система состояла из абсолютно жестких элементов;

2) в системах, статически определимых, реакции определяются так, как если бы элементы системы были абсолютно жесткими.

Аксиома 5 (аксиома отвердевания). Равновесие нетвердого тела не нару­шится, если при тех же действующих на него силах оно затвердеет и станет абсолютно твердым.

 На основании этой аксиомы результа­ты, полученные в статике абсолютно твердого тела, можно применять к дефор­мируемым телам.

 Утверждение, обратное аксиоме 5, неверно (если тело пе­рестает быть твер­дым, то его равновесие может нарушиться).

СВЯЗИ. РЕАКЦИИ СВЯЗЕЙ.

    Тела, рассматриваемые в механике, могут быть свободными и несвободными. По определению, приведенному выше, тело, которое не скреплено с другими телами и может совершать из данного положения любые перемещения в пространстве, называется свободным.

    Тело, перемещениям которого в пространстве препятствуют какие-нибудь другие, скрепленные или соприкасающиеся с ним тела, называется несвободным.

    Необходимо помнить, что разделение тел на свободные и несвободные условно, так как фактически свободных тел в природе нет. Если тело не свободно, то говорят, что на него наложены связи. Все то, что ограничивает перемещения данного тела в пространстве, будем называть связью.     Следует подчеркнуть, что определение связей, как некоторых других тел, ограничивающих свободу перемещений данного тела, является неполным. Наиболее общее и полное определение связей будет дано в разделе динамики.    Если тело не может покинуть связь, то связь называется удерживающей. Примером может служить проволока с надетым на нее кольцом. Если же тело при некоторых перемещениях может покинуть связь, то она называется односторонней или неудерживающей: например, тело, лежащее на столе, может перемещаться по столу —связь не нарушается, но если поднять его, сняв со стола, связь нарушится.    Тело под действием приложенных к нему сил давит на связи, но перемещению тела препятствуют наложенные на него связи» отклоняющие движение от того направления, которое имело бы тело, свободное от связей.    Сила, с которой связь действует на тело, называется реакцией связи. Если считать силу, с которой тело действует на связь, действием, то сила реакции связи является противодействием. Согласно закону о равенстве действия и противодействия реакция связи равна по модулю силе действия тела на связь, а ее направление противоположно тому направлению, в котором данная связь препятствует перемещению тела. Однако эти силы нельзя считать уравновешенными, хотя они равны по модулю и направлены противоположно, так как точки приложения этих двух сил принадлежат различным телам: действие (давление) приложено к связи, а реакция связи (противодействие) приложена к телу, равновесие которого мы рассматриваем.    Таким образом, все силы, действующие на тело, можно разделить на две группы: силы активные, или задаваемые (сила тяжести, сила упругости сжатой или растянутой пружины и т. п.) и реакции связей. К первой группе следует относить все силы, не являющиеся реакциями связей.    Характерной особенностью активных сил является то, что модуль и направление каждой из них наперед известны и непосредственно не зависят от действия других, приложенных к данному телу сил, а также от движения тела и характера наложенных на него связей. Силы реакции связей зависят от действия приложенных активных сил, а также от движения тела и характера наложенных на него связей

   Реакции связей возникают только тогда, когда тело, на которое заложены связи, под действием активных сил оказывает давление на эти связи. Как только давление прекращается, перестают действовать на тело и силы реакции связей. В этом смысле силы реакции связей называются пассивными, так как в отличие от активных они сами не могут вызвать движение тела.

   Изучая движение или покой какого-либо тела, мы должны учитывать все силы, которые действуют на это тело,— как активные, так и реакции связей.

   В статике почти всегда приходится рассматривать равновесие несвободного тела. Определение реакций связей для тела, находящегося в равновесии, является одной из основных задач статики.

   Чтобы определить реакцию связи, необходимо знать ее модуль, направление и точку приложения. Модуль каждой силы реакции связи всегда зависит от действующих на тело активных сил и является наперед неизвестным. Направление же сил реакций связей известно лишь для некоторых типов связей. Если связь препятствует перемещению тела только в одном каком-нибудь направлении, то направление ее реакции противоположно этому направлению. Если же связь препятствует перемещениям тела по многим направлениям, то направление силы реакции связи наперед неизвестно и может быть (так же, как и модуль силы реакции) установлено в результате решения соответствующей задачи статики. Точка приложения реакции связи известна.

    Следует подчеркнуть, что если связь не препятствует перемещению тела в некотором направлении, то ее реакция не имеет составляющей в этом направлении.

Связи и их реакции

    Тело, которое может совершать из данного положения любые перемещения в пространстве, называется свободным.

    Тело, перемещениям которого препятствуют какие-нибудь другие, скрепленные или соприкасающиеся с ним тела, называется несвободным. Все то, что ограничивает перемещение данного тела, называют связью.

    Сила, с которой данная связь действует на тело, препятствующая тем или иным его перемещениям, называется реакцией связи. Реакция связи направлена в сторону противоположную той, куда связь не дает перемещаться телу.

    Принцип освобождаемости от связей: несвободное твердое тело можно рассматривать как свободное, если его мысленно освободить от связей, заменив их действие реакциями. В статике этот принцип позволяет рассматривать равновесие несвободного твердого тела как свободного под действием активных (заданных) сил и реакций связей.

    Рассмотрим наиболее часто встречающиеся типы связей на плоскости и направления их реакций.