21.Скалярное произведение векторов. Свойства.

скалярным произведением двух нулевых векторов а и б называется число, равное произведению длин этих векторов на косинус угла между ними.

Обозначается. а*б=|a|*|b|*cosf

Скалярное произведение векторов равно модулю одного из них, умноженному на проекцию другого на ось, сонаправленную с первым вектором. ab=|a|*ПРAb=|b|*ПРБa

Свойства

• теорема косинусов легко выводится с использованием скалярного произведения:

• Угол между векторами:

• Оценка угла между векторами:

в формуле   знак определяется только косинусом угла (нормы векторов всегда положительны). Поэтому скалярное произведение > 0, если угол между векторами острый, и < 0, если угол между векторами тупой.

• Проекция вектора 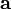  на направление, определяемое единичным вектором  :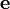

,

• условие ортогональности (перпендикулярности) векторов   и  :

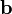• Площадь параллелограмма, натянутого на два вектора   и  , равна

22.Выражение скалярного произведения векторов в координатной форме.

Если векторы   и   заданы своими координатами в базисе  :  ,  ,

То их скалярное произведение определяется формулой:

.

Доказательство.

.

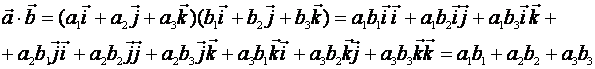Т.к.                                                                

                                        

Теорема доказана.

23.Векторное произведение векторов. Свойства.

Векторным произведением вектора   на вектор   называется вектор, обозначаемый символом   и определяемый следующими тремя условиями:

1). Модуль вектора   равен  , где   - угол между векторами   и  ;

2). Вектор   перпендикулярен к каждому из вектора   и  ;

3). Направление вектора   соответствует «правилу правой руки».

Векторное произведение зависит от порядка сомножителей, именно: .

Модуль векторного произведения   равен площади S параллелограмма, построенного на векторах   и  : .

Само векторное произведение может быть выражено формулой ,где   - орт векторного произведения. Векторное произведение   обращается в нуль тогда и только тогда, когда векторы   и   коллинеарны. В частности,  .

Если система координатных осей правая и векторы   и   заданы в этой системе своими координатами:

,  ,

то векторное произведение вектора   на вектор   определяется формулой или

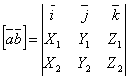
25. Смешанное произведение трех векторов.

Смешанным произведением трех векторов  ,  ,   называется число, равное векторному произведению  , умноженному скалярно на вектор  , то есть  .

Имеет место тождество , ввиду чего для обозначения смешанного произведения   употребляется более простой символ  . Таким образом,

,  .

Если векторы  ,  ,   компланарны (и только в этом случае), смешанное произведение   равно нулю; иначе говоря, равенство есть необходимое и достаточное условие компланарности векторов  ,  ,  .

26. Выражение смешанного произведения векторов через координаты векторов.

Если векторы  ,  ,   заданы своими координатами: ,  ,  ,то смешанное произведение   определяется формулой

.

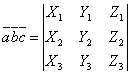27. Условия перпендикулярности, коллинеарности, компланарности векторов.

Условие перпендикулярности векторов:

1.Векторы являются перпендикулярными тогда и только тогда, когда их скалярное произведение равно нулю.

2.Даны два вектора a (xa;ya) и b (xb;yb). Эти векторы будут перпендикулярны, если выражение xaxb + yayb = 0.

Условие коллинеарности векторов

1.Векторы коллинеарны, если абсцисса первого вектора относится к абсциссе второго так же, как ордината первого — к ординате второго.

2.Даны два вектора a (xa;ya) и b (xb;yb). Эти векторы коллинеарны, если xa =   xb и ya =   yb, где  R.

Условия компланарности векторов

1.Три вектора компланарны, если их смешанное произведение равно нулю.

2.Три вектора компланарны, если они линейно зависимы.