8. Ранг матрицы

Наибольший из порядков миноров данной матрицы, отличных от нуля, называется рангом матрицы. Обозначается r,r(A), rang A.

Минор, порядок которого определят ранг матрицы, называется базисным. У матрицы может быть несколько базисных миноров.

Свойства ранга марицы:

1. при транспонировании матрицы её ранг не меняется.

2. Если вычеркнуть из матрицы нулевой ряд, то ранг матрицы не изменится.

3. Ранг матрицы не изменится при элементарных преобразованиях матрицы.

Ранг канонической матрицы равен числу единиц на главной диагонали. На этом основан один из способов вычисления ранга матрицы.

9.Система линейных алгебраических уравнений (слу). Теорема Кронекера-Капелли.

Система линейных алгебраических уравнений, содержащей m уравнений и n неизвестных, называется система вида. 

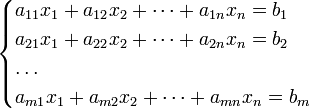
Здесь   — неизвестные, которые надо определить. Коэффициенты системы   и её свободные члены   предполагаются известными. Индексы коэффициента   системы обозначают номера уравнения   и неизвестного  , при котором стоит этот коэффициент.

Система называется однородной, если все её свободные члены равны нулю,  , иначе — неоднородной.

Система называется квадратной, если число   уравнений равно числу   неизвестных.

Решение системы уравнений — совокупность   чисел  , таких что подстановка каждого   вместо   в систему обращает все её уравнения в тождества.

Система называется совместной, если она имеет хотя бы одно решение, и несовместной, если у нее нет ни одного решения. Совместная система может иметь одно или более решений.

Решения   и   совместной системы называются различными, если нарушается хотя бы одно из равенств:

Совместная система называется определенной, если она имеет единственное решение; если же у нее есть хотя бы два различных решения, то она называется неопределенной. Если уравнений больше, чем неизвестных, она называется переопределённой.

Теорема Кронекера–Капелли (критерий совместности системы линейных уравнений). Для того чтобы система линейных уравнений была совместной, необходимо и достаточно, чтобы ранг матрицы системы был равен рангу ее расширенной матрицы, т.е.  .

Замечание. Если ранг матрицы совместной системы равен числу неизвестных, то система имеет единственное решение, если же ранг меньше числа неизвестных, то система имеет множество решений.

.

10.Решение слу матричным методом.

Ма́тричный метод решения (метод решения через обратную матрицу) систем линейных алгебраических уравнений с ненулевым определителем состоит в следующем.

Пусть дана система линейных уравнений с   неизвестными (над произвольным полем):

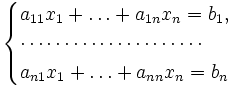
Тогда её можно переписать в матричной форме:

, где   — основная матрица системы,   и   — столбцы свободных членов и решений системы соответственно:

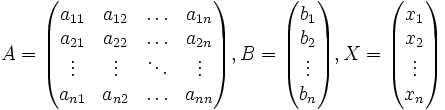
Умножим это матричное уравнение слева на   — матрицу, обратную к матрице  : 

Так как  , получаем  . Правая часть этого уравнения даст столбец решений исходной системы. Условием применимости данного метода (как и вообще существования решения неоднородной системы линейных уравнений с числом уравнений, равным числу неизвестных) является невырожденность матрицы A. Необходимым и достаточным условием этого является неравенство нулю определителя матрицы A:

Для однородной системы линейных уравнений, то есть когда вектор  , действительно обратное правило: система   имеет ненулевое решение только если  . Такая связь между решениями однородных и неоднородных систем линейных уравнений носит название альтернативы Фредгольма.