
Тераційні методи
Ітераційні методи встановлюють процедуру уточнення певного початкового наближення до розв'язку. При виконанні умов збіжності вони дозволяють досягти будь-якої точності просто повторенням ітерацій. Перевага цих методів у тому, що часто вони дозволяють досягти розв'язку з наперед заданою точністю швидше, а також розв'язувати більші системи рівнянь. Суть цих методі полягає в тому, щоб знайти нерухому точку матричного рівняння:
![]() ,
,
еквівалентного
початковій системі лінійних алгебраїчних
рівнянь. При ітерації ![]() в
правій частині рівняння заміняється,
наприклад, у методі
Якобі (метод простої ітерації) на
наближення, знайдене на попередньому
кроці:
в
правій частині рівняння заміняється,
наприклад, у методі
Якобі (метод простої ітерації) на
наближення, знайдене на попередньому
кроці:
![]() .
.
Збіжність
ітераційної процедури досягається
вибором матриці ![]() ,
що залежить від задачі. Умови збіжності
конкретні для кожного конктретного
метода.
,
що залежить від задачі. Умови збіжності
конкретні для кожного конктретного
метода.
36.
Як відомо, цій системі відповідають дві матриці. Основна матриця системи
 ;
;
розширена матриця системи


 .
.
Для кожної системи лінійних рівнянь можна скласти розширену матрицю і, навпаки, за допомогою розширеної матриці можна відновити систему лінійних рівнянь.
Кожному еквівалентному перетворенню системи лінійних рівнянь відповідає перетворення розширеної матриці системи.
Перестановці рівнянь в системі відповідає перестановка рядків розширеної матриці.
Перестановці змінних в рівняннях відповідає перестановка стовпчиків основної матриці системи.
Викресленню нульового рівняння відповідає викреслення з розширеної матриці нульового рядка.
Ранг матриці - найвищий з порядків мінорів цієї матриці, відмінних від нуля
37.
Теорема (Кронекера – Капелі). Система лінійних рівнянь сумісна тоді і тільки тоді, коли ранг її основної матриці дорівнює рангу розширеної матриці.
Доведення. Будемо розглядати систему лінійних рівнянь.
 Цю
систему можна переписати так.
Цю
систему можна переписати так. .
.
38.
Матриця називається ступінчастою, якщо виконані наступні умови: після нульової рядки йдуть тільки нульові рядки; перший ненульовий елемент в кожній наступній рядку розташований правіше, ніж у попередній.
Ранг матриці - найвищий з порядків мінорів цієї матриці, відмінних від нуля.
Ранг матриці - Розмірність образу d i m (i m (A)) лінійного оператора, якому відповідає матриця.
Зазвичай
ранг матриці A позначається ![]() (
( ![]() )
Або
)
Або ![]() .
.
39.
Метод Гауса — Жордана використовується для розв'язання систем лінійних алгебраїчних рівнянь, знаходження оберненої матриці, знаходження координат вектора у заданому базисі, відшукання рангу матриці. Метод є модифікацією методу Гауса. Названий на честь Гауса та німецького математика та геодезиста Вільгельма Йордана.
Алгоритм:
Обирається перша зліва колонка, що містить хоч одне ненульове значення.
Якщо верхнє число у цій колонці - нуль, то обмінюється увесь перший рядок матриці з іншим рядком матриці, де у цій колонці нема нуля.
Усі елементи першого рядка діляться на верхній елемент обраної колонки.
Від рядків, що залишились, віднімається перший рядок, помножений на перший елемент відповідного рядка, з метою отримання у якості першого елемента кожного рядка (крім першого) нуля.
Далі, повторюємо ці операції із матрицею, отриманою з початкової матриці після викреслювання першого рядка та першого стовпчика.
Після повторення операцій n-1 разів отримаємо верхню трикутну матрицю.
Віднімаємо від передостаннього рядка останній рядок, помножений на відповідний коефіцієнт, щоб у передостанньому рядку залишилась лише 1 на головній діагоналі.
Повторюємо попередній крок для наступних рядків. У результаті отримуємо одиничну матрицю і рішення на місці вільного вектора (над ним необхідно виконувати ті самі перетворення).
Приклад
Розв'яжемо систему рівнянь:
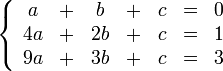
Запишемо її у вигляді матриці 3×4, де останній стовпчик є вільним членом:
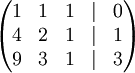
Виконаємо такі дії:
До рядка 2 додамо: -4 * рядок 1.
До рядка 3 додамо: -9 * рядок 1.
Отримаємо:
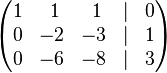
До рядка 3 додамо: -3 * рядок 2.
Рядок 2 ділимо на -2
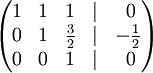
До рядка 1 додамо: -1 * рядок 3.
До рядка 2 додамо: -3/2 * рядок 3.
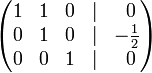
До рядка 1 додамо: -1 * рядок 2.
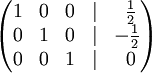
У правому стовпчику отримаємо рішення:
![]() .
.
40.
Система лінійних рівнянь називається однорідною, якщо вільні члени всіх рівнянь системи дорівнюють нулю.
42.
