Канонічне рівняння еліпса

Властивості

• Якщо F ₁ і F ₂ - Фокуси еліпса, то для будь-якої точки X, що належить еліпсу, кут між дотичною в цій точці і прямий (F ₁ X) дорівнює куту між цією дотичній і прямий (F ₂ X) .

• Пряма, проведена через середини відрізків, відсічених двома паралельними прямими, що перетинають еліпс, завжди буде проходити через центр еліпса. Це дозволяє побудовою за допомогою циркуля і лінійки легко отримати центр еліпса, а надалі осі, вершини і фокуси.

• Еволюти еліпса є астроіда.

• Точки перетину еліпса з осями є його вершинами.

22.

Гіпербола - геометричне місце точок M Евклідової площини, для яких абсолютне значення різниці відстаней від M до двох виділених точок F ₁ і F ₂ (Званих фокусами) постійно. Точніше,

 причому | F ₁ F ₂ |> 2 a> 0.

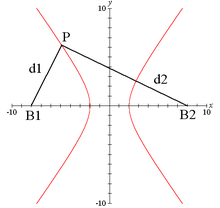
 канонічним рівнянням гіперболи

Властивості

Оптичне властивість. Світло від джерела, що знаходиться в одному з фокусів гіперболи, відбивається другої гілки гіперболи таким чином, що продовження відбитих променів перетинаються в другому фокусі.

Інакше кажучи, якщо F ₁ і F ₂ фокуси гіперболи, то дотична в будь-якої точки X гіперболи є бісектрисою кута   .

Для будь-якої точки що лежить на гіперболі відношення відстаней від цієї точки до фокусу до відстані від цієї ж точки до директриси є величина постійна.

Гіпербола володіє дзеркальною симетрією щодо дійсної та уявної осей, а також обертальної симетрією при повороті на кут 180 навколо центру гіперболи.

Кожна гіпербола має сполучену гіперболу, для якої дійсна і уявна осі міняються місцями, але асимптоти залишаються колишніми. Це відповідає заміні a і b один на одного у формулі, яка описує гіперболу. Сполучена гіпербола не є результатом повороту початкової гіперболи на кут 90 ; обидві гіперболи розрізняються формою.

23.

Пара́бола — геометричне місце точок, що рівновіддалені від точки і прямої. Одна з кривих другого порядку.

Точка зветься фокусом, а пряма - директрисою.

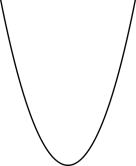
Канонічне рівняння параболи в прямокутній системі координат:

 (або  , якщо поміняти місцями осі).

Квадратне рівняння   при 

Властивості:

• Парабола - крива другого порядку.

• Вона має вісь симетрії, що називається віссю параболи. Вісь проходить через фокус і перпендикулярна директрисі.

• Оптична властивість. Пучок променів, паралельних осі параболи, відбиваючись у параболі, збирається в її фокусі. І навпаки, світло від джерела, що знаходиться у фокусі, відображається параболою в пучок паралельних її осі променів.

• Для параболи 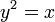  фокус знаходиться в точці (0,25; 0).

• Якщо фокус параболи відобразити щодо дотичній, то його образ буде лежати на директрисі.

• Парабола є антиподерою прямій.

• Всі параболи подібні. Відстань між фокусом і директрисою визначає масштаб.

• При обертанні параболи навколо осі симетрії виходить еліптичний параболоїд.

• Еволютою параболи є напівкубічна парабола.

24.

Площина - це поверхня, яка повністю містить, кожну пряму, що з'єднує будь-які її точки.

Площина — множина точок, рівновіддалених від двох заданих.

рівняння загальнеAx+By+Cz+d=0

ріняня площини у відрізках

рівняня прямої що проходить чер 3 точки

Нормальне (нормоване) рівняння площини

Рівняння площини, що проходить через точку   перпендикулярно до вектора  :

25.

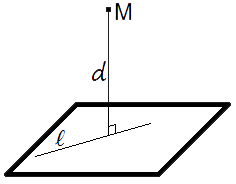
Відстань від точки до площини — дорівнює довжині перпендикуляра, опущеного з точки на площину.

Якщо задано рівняння площини Ax+ By+ Cz + D = 0, то відстань від точки M(M_x, M_y, M_z) до площини можна знайти використовуючи наступну формулу

d  =	|A·Mx+ B·My + C·Mz+ D|
	(A2 + B2 + C2)1/2

26.

Пряма лінія у просторі

Пряма задана загальними рівняннями

П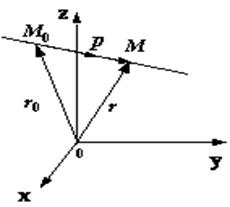 ряму можна задавати, як лінію перетину двох площин:

  параметричне рівняння прямої у просторі.

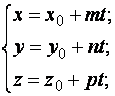
 – канонічні рівняння прямої у просторі.

• Через будь-які три точки, що не належать одній прямій, можна провести одну і тільки одну площину.

• Дві площини, що мають спільну точку, перетинаються по прямій, яка містить цю точку.

• Якщо площині належать дві точки прямої, то і уся пряма належить цій площині.

27.

дві прямі а і в в просторі можуть перетинатися, бути паралельними, бути мимобіжними.

Дві площини називаються паралельними, якщо вони не перетинаються. Уявлення про паралельні площини дають підлога і стеля класної кімнати, дві протилежні стіни класної кімнати, поверхня стола і площина підлоги.

Якщо площини α і β паралельні, то пишуть: α іі β.

Ми знаємо, що якщо дві різні площини мають спільну точку, то вони перетинаються по прямій, яка проходіть через цю точку.

Випадки взаємного розміщення прямої і площини:

Площина α не має спільних точок із прямою а. Пряма і площини, які не мають спільних точок, називаються паралельними, позначаються аІІα

Площина α має з прямою а тільки одну спільну точку. У цьому випадку говорять, що пряма а і площина α

Пряма а лежить у площині α

28.

е 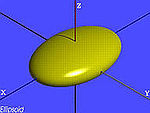ліпсоїд

   Сфера

Еліптичний параболоїд

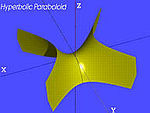
Гіперболічний параболоїд

Конус

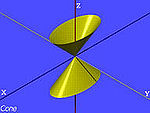
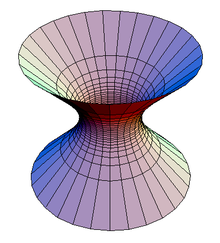
  Однопорожнинний гіперболоїд

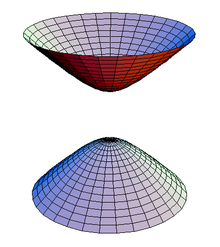
  двопорожнинний гіперболоїд

29.

Ве́кторний (ліні́йний) про́стір — основне поняття лінійної алгебри, узагальнення множини всіх векторів на площині чи в просторі з операціями додавання векторів тамноження вектора на скаляр.

У довільному векторному просторі не визначені операції скалярного, векторного добутку; норми чи метрики. Ці операції можуть вводитись як додаткові структури. Проте векторні простори із скалярним або ермітовим скалярним добутком відіграють важливу роль як у лінійній алгебрі, так і поза її межами, див. напр. гільбертів простір.

Прикладами векторних просторів над полем R дійсних чисел можуть бути множини векторів на площині чи в просторі

30.

Лінійно незалежні вектори (лінійна незалежність множини) — множина векторів, які не утворюють нетривіальних лінійних комбінацій рівних нулю.

Якщо існує така лінійна комбінація векторів рівна нулю з хоча б одним  , то   називається лінійно залежною.

• Якщ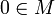о  , то   є лінійно залежна.

• Якщо   лінійно незалежна, то   лінійно незалежна для всіх  .

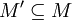• Якщо   лінійно залежна, то   лінійно залежна для всіх  .

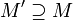• Якщо до системи входить , то система лінійно залежна.

• Система векторів лінійно залежна тоді і тільки тоді, коли принаймні один з векторів системи лінійно виражається через інші

• Якщо деяка підсистема системи векторів лінійно залежна, то і вся система лінійно залежна.

• Будь-яка підсистема лінійно незалежної системи векторів лінійно незалежна.

31.

У разі векторного простору скінченної розмірності над полем дійсних чисел дві системи координат вважаються пов'язаними додатньо, якщо додатній визначник матриці переходу від однієї з них до іншої.

Розмірністю скінченновимірного векторного простору 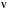над полем називається число, що дорівнює найбільшій кількості лінійно незалежних векторів з простору .

32.

підпростір векторного простору переліз сума пряма сумаПідпростором векторного простору називається непорожня підмножина векторів простору, яка сама утворює векторний простір. V. Сумою підросторівV1+V2 називається множина {x+x2|x1,x2єV2}. ПеретиномпідпросторівV1V2 називаєтьсямножинавекторів, яківходятьодночасно до V1 і V2. Сума й перетинпідпросторів є підпросторами простору V // Сума двохпідпросторівV1 і V2називається прямою сумою, якщо для кожного вектора з просторуV1+V2 існуєоднозначнезображення у виглядісуми вектора з V1 і вектора з V2, тежсаме, що з рівностіx +y=0 при xєV1yєV2 слідуєx=0y=0. Пряма сума позначаєтьсяV10(+в нулю)V2.

33.

Скалярним добутком двох векторів a та b звуть число, що дорівнює добуткові довжин цих векторів на косинус кута між ними:

Для   векторного простору над полем комплексних чисел стандартний скалярний добуток векторів   визначається як відображення, що задовільняє наступним умовам:

де риска над комплексним числом позначає комплексно-спряжене число.

Інший варіант скалярного добутку можна визначити як:

Таке визначення здебільшого використовується в фізиці.

Результати обох визначень є взаємно-спряженими комплексними числами. Для скалярного добутку вектора на самого себе, який визначає норму вектора, обидва визначення дають однаковий результат.