
Ортогональний базис — ортогональна система елементів лінійного простору зі скалярним добутком, що має властивість повноти.
Ортогональний базис — базис, складений з попарно ортогональних векторів.
Ортонормований базис задовольняє ще й умові одиничності норми всіх його елементів. Тобто це ортогональний базис з нормованими елементами.
ортогональний базис - В скінченновимірному унітарному векторному просторі розмірності n, кожна ортонормована система із n векторів утворює ортонормований базис.
В
кожному гільбертовому
просторі ![]() ,
ортонормована система векторів
,
ортонормована система векторів ![]() утворює
ортонормований базис
утворює
ортонормований базис
1.
Основні поняття теорії множин.
Множина – це сукупність об'єктів спільної природи. Її можна задати списком, тобто переліком її елементів, або вказавши спільну для елементів множини ознаку чи властивість. Множина називається скінченою або нескінченною, в залежності від того скінчену чи нескінченну к-ть елементів вона містить. Для позначення множин – А,В, для позначення елементів множини а,b. Множина, що не містить жодного елемента називається порожньою і позначається . є А ( - є елемент множини А, є – символ приналежності). А – множина називається підмножиною множини В, якщо вона складається з усіх, або деяких елементів множини В, при цьому записується А с В
(с – символ включення). А с А – будь яка множина є підмножиною самої себе. Дві множини А та В називаються рівними А=В, якщо кожний елемент множини А є елементом множини В і навпаки.
(Приклад: А={x є R : -1 x 2}. А є множиною дійсних чисел, що задовольняють таку нерівність. Задати таку множину списком – неможливо. ē – не належить. - квантор загальності і читається так: для кожного, для будь-якого, для всіх. - квантор існування. - не існує.
і - символ об'єднання і перетину множин, при цьому об'єднанням двох множин А та В називається множина С, С= А В, яка складається з елементів, що належать, хоча-би одній множині А та В. Графічно об'єднання двох множин можна зобразити за допомогою діаграми Вєнни. Перетином двох множин А та В називається множина С, С = А В, яка складається з елементів, що належать і множині А і множині В. Різницею двох множин А та В називається множина С, С = А \ В, яка складається з тих елементів множини А, які не належать множині В.
Зауважимо, що А с В; В с С => А с С – властивість транзиторності. => – символ для позначення слова "випливає". <=> – знак рівносильності.
2.
Відно́шення еквівале́нтності в математиці — бінарне відношення, яке є рефлексивне, симетричне та транзитивне.
приклад: Відношення рівності на будь-якій множині M є відношенням еквівалентності.
Відношення рівнопотужності множин є еквівалентністю.
Рівність (" ![]() "),
Тривіальне відношення еквівалентності
на будь-якому множині, зокрема, дійсних
чисел.
"),
Тривіальне відношення еквівалентності
на будь-якому множині, зокрема, дійсних
чисел.
Порівняння за модулем, ("а ≡ b (mod n)")
Прикладом відношення еквівалентності є відношення рівності чисел чи множин,
геометричне відношення подібності трикутників, відношення паралельності прямих у
евклідовому просторі.
Нехай ≡ - відношення еквівалентності на A і x∈A. Тоді підмножина
елементів множини A, які еквівалентні x, називається класом еквівалентності для x:
[x]≡ = {y | y∈A, x ≡ y}
Сукупність множин {Bi|i∈I} називається розбиттям множини A, якщо Bi=A і Bi∩Bj = ∅ для i≠j. Множини Bi, i∈I є підмножинами множини A і називаються класами, суміжними класами, блоками або елементами розбиття. Очевидно, що кожний елемент a∈A належить одній і тільки одній множині Bi, i∈I.
3.
Відно́шення поря́дку в математиці — бінарне відношення, яке є транзитивним та антисиметричним.
![]() (транзитивність),
(транзитивність),
![]() (антисиметричність).
(антисиметричність).
Відношення порядку називається нестрогим, якщо воно рефлексивне
![]() .
.
І навпаки, відношення строгого порядку є антирефлексивним
![]() .
.
Відношення порядку називається повним (лінійним), якщо
![]() (повне
відношення).
(повне
відношення).
Повнота (лінійність) відношення порядку означає його рефлексивність, тому такий порядок завжди нестрогий.
Якщо умова повноти не виконується, і порядок є нестрогим, то відношення називають відношенням часткового порядку.
Зазвичай
відношення строгого порядку (повного
чи часткового) позначається знаком <,
а відношення нестрогого порядку знаком ![]() .
.
Впорядко́вана
множина́ — множина для
будь-яких двох елементів ![]() ,
, ![]() якої
встановлено одне з наступних відношень
порядку:
якої
встановлено одне з наступних відношень
порядку:
або ![]() (
не
перевищує
),
або
(
не
перевищує
),
або ![]() (
не
перевищує
),
(
не
перевищує
),
які володіють наступними властивостями:
рефлексивність: будь елемент не перевершує самого себе;
антисиметричність: якщо не перевершує , а не перевершує , то елементи і збігаються;
транзитивність: якщо не перевершує , а не перевершує
 ,
то
не
перевершує
.
,
то
не
перевершує
.
запис: Впорядковані (скінченні або такі, елементи яких можна перерахувати) множини часто записують, розташовуючи їх елементи в заданому порядку в круглих дужках. Наприклад, записи
(1; 2; 3) і (2; 1; 3) (1)
представляють різні скінченні впорядковані множини, які можна отримати з однієї і тієї ж множини {1; 2; 3}, впорядковуючи її двома різними способами. Для запису скінченної впорядкованої множини у виді, аналогічному (1), необхідно вказати перший елемент впорядкованої множини і вказати порядок (правило) розташування наступних елементів.
4.
Алгебраїчна система (алгебраїчна структура) — в математиці це непорожня множина з заданим на ній набором операцій та відношень, що задовільняють деякій системі аксіом.
![]() -арна операція
-арна операція ![]() на
на ![]() —
це відображення прямого
добутку
екземплярів
множини в саму множину
—
це відображення прямого
добутку
екземплярів
множини в саму множину ![]() .
За визначенням, нуль-арна
операція —
це просто виділений елемент множини.
.
За визначенням, нуль-арна
операція —
це просто виділений елемент множини.
Найчастіше розглядають унарні і бінарні операції, як найпростіші. Але для потреб топології, алгебри, комбінаторики вивчають операції більшої арності, наприклад, теоріяоперад і алгебр над ними (мультиоператорних алгебр).
Біна́рна опера́ція (бінарний оператор) — це математичний об'єкт, що складається з двох величин і певної дії над ними.
Бінарну операцію також називають двоелементною або двомісною операцією. (дивись Містність операції).
Бінарною
операцією на множині ![]() є відображення декартового
добутку
є відображення декартового
добутку ![]() в
множину
:
в
множину
:
![]()
Бінарні операції часто записують за допомогою інфікса, наприклад, a * b, a + b, a • b, замість функціонального запису f(a, b).
Іноді елементи просто пишуть одне за одним без інфікса: ab.
Бінарні операції є наріжним каменем алгебраїчних структур, що їх вивчають в абстрактній алгебрі.
Бінарні операції входять в означення таких структур, як групи, моноїди, напівгрупи, кільця, поля тощо.
За визначенням: магма є множиною з довільною бінарною операцією на ній.
Багато бінарних операцій, що становлять інтерес, є комутативними чи асоціативними. Багато з них також мають нейтральний елемент та обернені елементи.
Типовими прикладами таких бінарних операцій є додавання (+) і множення (*) чисел та матриць.
Прикладами некомутативних бінарних операцій є віднімання (-), ділення (/), піднесення до степеня (^), композиція функцій.
Деякі операції мають властивість ідемпотентності чи дистрибутивності.
приклади бінарних операцій
арифметичні дії з числами: додавання, віднімання, множення, ділення;
додавання, множення матриць;
об'єднання і перетин множин.
5.
Групою називається множина G,
на якій визначено бінарну
операцію ![]() ,
що зазвичай називають множенням і
позначають
,
що зазвичай називають множенням і
позначають ![]() або
або ![]() ,
і має такі властивості:
,
і має такі властивості:
Асоціативність: для довільних елементів a, b, c групи G виконується рівність
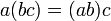
Існування нейтрального елемента: існує елемент e такий, що для кожного елемента a групи G виконується
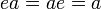
Існування оберненого елемента: для кожного елемента a групи існує елемент
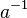 такий,
що
такий,
що 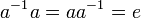 .
.
Операція множення в групі не обов'язково є комутативною.
Таким чином, група є моноїдом, у якому для кожного елемента існує обернений.
Властивості абстрактних груп вивчаються в теорії груп. Провідну роль у геометрії, зокрема в диференціальній геометрії і топології, відіграють дії груп на різноманітних просторах (див. також групи перетворень).
Підгрупою групи G називається підмножина ![]() групи
групи ![]() ,
що сама є групою щодо операції, визначеної
в
.
,
що сама є групою щодо операції, визначеної
в
.
Підмножина групи є її підгрупою тоді і тільки тоді, коли вона задовольняє такі умови:
містить добуток будь-яких двох елементів з ,
містить разом зі всяким своїм елементом
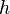 обернений до
нього елемент
обернений до
нього елемент 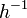 .
.
У разі скінченних і періодичних груп перевірка умови 2 є зайвою.
Еквівалентно є підгрупою, якщо виконується умова:
![]()
приклад:
Підмножина групи , що складається з одного елементу
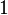 ,
буде, очевидно, підгрупою, і ця підгрупа
називається одиничною підгрупою
групи
.
,
буде, очевидно, підгрупою, і ця підгрупа
називається одиничною підгрупою
групи
.Сама також є своєю підгрупою.
Нехай G абелева група елементами якої є
![]()
6.
Кільце́ — в абстрактній алгебрі це алгебраїчна структура, в якій визначені операції додавання та множення з властивостями подібними до додавання і множення цілих чисел. Вивченням властивостей кілець присв'ячена теорія кілець.
Кільце ![]() —
це множина з
двома бінарними
операціями,
що звичайно позначаються "
—
це множина з
двома бінарними
операціями,
що звичайно позначаються "![]() "
та "
"
та "![]() "
і називаються додаванням та множенням,
яка задовільняє наступній системі аксіом:
"
і називаються додаванням та множенням,
яка задовільняє наступній системі аксіом:
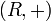 є комутативною групою.
Її називають адитивною
групою кільця і нейтральний
елемент в
ній позначають як 0 (нуль);
є комутативною групою.
Її називають адитивною
групою кільця і нейтральний
елемент в
ній позначають як 0 (нуль);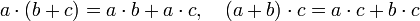 (дистрибутивність додавання
щодо множення);
(дистрибутивність додавання
щодо множення);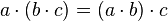 (асоціативність множення);
(асоціативність множення);в
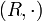 існує
нейтральний елемент 1 (одиниця),
що задовільняє:
існує
нейтральний елемент 1 (одиниця),
що задовільняє: 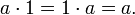
Розглядаються також кільця, у яких не задовільняється асоціативність множення, наприклад, кільця (або алгебри) Лі. У такому разі, кільця, в яких множення асоціативне, називають асоціативними кільцями.
Кільця,
що задовольняють на
вимогу комутативності множення ![]() називають комутативними
кільцями.
Не всі кільця є комутативними, наприклад,
кільцематриць чи кватерніонів.
називають комутативними
кільцями.
Не всі кільця є комутативними, наприклад,
кільцематриць чи кватерніонів.
властивості:
якщо
кільце містить більше одного елемента,
то ![]()
![]()
![]()
![]() якщо
і
якщо
і ![]() обидва
мають обернені елементи. Отже множина
всіх оборотних елементів кільця є
замкненою відносно множення, і тому
утворює групу, що позначається
обидва
мають обернені елементи. Отже множина
всіх оборотних елементів кільця є
замкненою відносно множення, і тому
утворює групу, що позначається ![]() .
.
Підмножина К1 кільця К називається підкільцем кільця К, якщо К1 є кільцем відносно операцій додавання і множення, визначених в кільці К. Перевірка того, що дана підмножина кільця є його підкільцем, включає вияснення, чи різниця й добуток довільних двох елементів підмножини К1 належить до К1. Приклади. 1. Кільце парних чисел - підкільце кільця цілих чисел. 2. Кільце цілих чисел - підкільце кільця раціональних чисел. 3. Кільце раціональних чисел - підкільце кільця дійсних чисел.
7.
По́ле (англ. field — поле, нім. körper — тіло) — це алгебраїчна структура, для якої визначені дві пари бінарних операцій: додавання/віднімання та множення/ділення, причому ці операції задовольняють умовам, схожим на властивості арифметичних операцій над раціональними, дійсними або комплексними числами.
Поле
— це комутативне кільце ![]() з одиницею,
в якому кожний ненульовий
елемент
з одиницею,
в якому кожний ненульовий
елемент ![]() має обернений
має обернений ![]() ;
як правило, в означенні вимагають також
існування принаймні одного ненульового
елемента.
;
як правило, в означенні вимагають також
існування принаймні одного ненульового
елемента.
Якщо
підмножина
поля ![]() сама
утворює поле щодо операцій в
(з
тими самими нулем і одиницею),
то
називається підполем
сама
утворює поле щодо операцій в
(з
тими самими нулем і одиницею),
то
називається підполем ![]() а
— розширенням
поля
.
Позначається
а
— розширенням
поля
.
Позначається ![]()
Приклад:
Полем є: раціональні числа
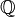 , дійсні
числа
, дійсні
числа 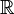 , комплексні
числа
, комплексні
числа 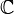 .
Кожне наступне з цих полів є розширенням
попереднього:
.
Кожне наступне з цих полів є розширенням
попереднього:
![]()
Так
само, множина всіх алгебраїчних
чисел замкнена
відносно алгебраїчних операцій, а тому
утворює поле, яке містить ![]() і
міститься в
і
міститься в ![]()
Якщо
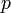 — просте
число,
то кільце
лишків
— просте
число,
то кільце
лишків 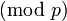 —
це скінченне
поле з
елементів,
яке позначається
—
це скінченне
поле з
елементів,
яке позначається
![]()
Називається — поле Галуа порядку , назване так на честь Евариста Галуа, який першим розглянув скінченні поля.
Мероморфні функції
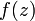 на
одиничному крузі
на
одиничному крузі 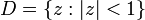 ,
з операціями поточкового додавання та
множення, утворюють поле.
,
з операціями поточкового додавання та
множення, утворюють поле.
8.
Натура́льні
чи́сла — числа,
що виникають природним чином при лічбі.
Це числа: 1, 2, 3, 4, … Множину натуральних
чисел прийнято позначати знаком ![]()
До арифметичних операцій над натуральними числами прийнято відносити такі операції:
операції:
Додавання: доданок + доданок = сума.
Множення: множник множник = добуток. Крім знака , для позначення множення використовується знак
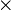 або
відсутність знака (у випадку, коли це
не спричинює двозначності запису).
або
відсутність знака (у випадку, коли це
не спричинює двозначності запису).Віднімання: зменшуване
 від'ємник = різниця.
При цьому, щоб результат також був
натуральним числом, зменшуване повинно
бути більшим за від'ємник (а якщо 0
відносити до натуральних чисел, до
допустима також рівність зменшуваного
та від'ємника). За означенням,
від'ємник = різниця.
При цьому, щоб результат також був
натуральним числом, зменшуване повинно
бути більшим за від'ємник (а якщо 0
відносити до натуральних чисел, до
допустима також рівність зменшуваного
та від'ємника). За означенням, 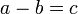 ,
якщо
,
якщо 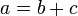 .
.Ділення: ділене / дільник = частка. За означенням,
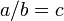 ,
якщо
,
якщо 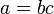 .
Ділення може позначатися також
горизонтальною рискою (ділене зверху,
дільник знизу) або двокрапкою. У багатьох
випадках ділення виводить за межі
множини натуральних і навіть цілих
чисел (див. Подільність).
Тому запроваджується також інша
операція.
.
Ділення може позначатися також
горизонтальною рискою (ділене зверху,
дільник знизу) або двокрапкою. У багатьох
випадках ділення виводить за межі
множини натуральних і навіть цілих
чисел (див. Подільність).
Тому запроваджується також інша
операція.Ділення з остачею: ділене / дільник = (частка, остача). За означенням, ділене = a, дільник = b, частка = q, остача = r, якщо
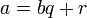 ,
, 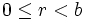 .
Така дія над натуральними числами
завжди здійсненна й однозначна, хоча
можливі значення для частки й остачі —
це натуральні числа та 0.
.
Така дія над натуральними числами
завжди здійсненна й однозначна, хоча
можливі значення для частки й остачі —
це натуральні числа та 0.
Операції додавання та множення є основними, а інші означаються через них, як описано вище; це характерно для будь-яких математичних структур з аналогічними операціями. Зазначимо також, що додавання та множення є замкненими операціями у множині натуральних чисел, оскільки вони завжди дають у результаті натуральне число (якщо були здійснені над натуральними числами); цього не можна сказати про віднімання та ділення.
основні властивості
Комутативність додавання:
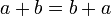
Комутативність множення:
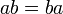
Асоціативність додавання:
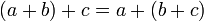
Асоціативність множення:
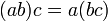
Дистрибутивність множення відносно додавання:
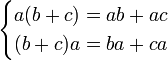
Математи́чна інду́кція — застосування принципу індукції для доведення теорем в математиці. Зазвичай полягає в доведенні вірності твердження стосовно одного знатуральних чисел, а потім всіх наступних.
Принцип
індукції полягає в тому, що
нескінченна послідовність тверджень ![]() ,
, ![]() ,
вірна якщо:
,
вірна якщо:
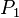 —
вірне,
та
—
вірне,
таіз правильності
 випливає
правильність
випливає
правильність 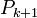 для
всіх k.
для
всіх k.Існує також варіація, так званий принцип повної математичної індукції. Ось його сувора формулювання:
Нехай є послідовність тверджень P 1 , P 2 , P 3 ,
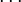 .
Якщо для будь-якого натурального n з
того, що істинні всі P 1 , P 2 , P 3 ,
, P n -
1 ,
Слід також істинність P n ,
То всі твердження в цій послідовності
істинні, тобто
.
Якщо для будь-якого натурального n з
того, що істинні всі P 1 , P 2 , P 3 ,
, P n -
1 ,
Слід також істинність P n ,
То всі твердження в цій послідовності
істинні, тобто  .
.У цій варіації база індукції виявляється зайвою, оскільки є тривіальним приватним випадком індукційного переходу. Дійсно, при n = 1 посилка
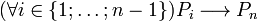 еквівалентна P 1 .
Принцип повної математичної індукції
є прямим застосуванням сильнішою трансфінітних
індукції.
еквівалентна P 1 .
Принцип повної математичної індукції
є прямим застосуванням сильнішою трансфінітних
індукції.
9.
Ко́мпле́ксні
чи́сла, — розширення поля дійсних
чисел,
зазвичай позначається
.
Будь-яке комплексне число може бути
представлене, як формальна сума ![]() ,
де
,
де![]() і
і ![]() —
дійсні числа,
—
дійсні числа, ![]() — уявна
одиниця[1].
— уявна
одиниця[1].
Комплексні числа утворюють алгебраїчно замкнуте поле — це означає, що многочлен ступеня n із комплексними коефіцієнтами має рівно n комплексних коренів (основна теорема алгебри). Це одна з головних причин широкого застосування комплексних чисел у математичних дослідженнях. Крім того, застосування комплексних чисел дозволяє зручно і компактно сформулювати багато математичних моделей, що застосовуються в математичній фізиці та природничих науках — електротехніці,гідродинаміці, картографії, квантовій механіці, теорії коливань і багатьох інших.
Арифметичні
дії виконуються аналогічно до дій з
многочленами, але з урахуванням
рівності ![]() .
Нехай
.
Нехай ![]() та
та ![]() —
комплексні числа. Тоді:
—
комплексні числа. Тоді:
Для комплексних чисел певним чином визначають також інші операції, наприклад, піднесення до довільного комплексного степеня, логарифмування, знаходженнясинуса, косинуса тощо. Деякі з цих операцій не є однозначними і ведуть до розгляду багатозначних функцій, які взагалі часто виникають при вивченні функцій комплексної змінної. Теорію про функції комплексної змінної часто називають комплексним аналізом. Одним зі способів означення елементарних функцій комплексної змінної є задання такої функції як суми степеневого ряду, в який можна розкласти аналогічну функцію дійсної змінної (див. Ряд Тейлора).
Зв'язані визначення
Нехай ![]() і
і ![]() — дійсні
числа,
такі, що комплексне число
— дійсні
числа,
такі, що комплексне число ![]() (звичайні
позначення). Тоді
(звичайні
позначення). Тоді
Числа
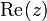 і
і  називаються
відповідно дійсною (Real)
і уявною (Imaginary)
частинами
називаються
відповідно дійсною (Real)
і уявною (Imaginary)
частинами 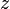 .
.Якщо
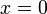 ,
то
називається
уявним або чисто уявним.
,
то
називається
уявним або чисто уявним.
Число
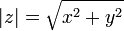 називається
модулем числа
.
Для дійсного числа модуль збігається
з його абсолютною величиною. Деякі
властивості модуля:
називається
модулем числа
.
Для дійсного числа модуль збігається
з його абсолютною величиною. Деякі
властивості модуля:
![]() ,
причому
,
причому ![]() тоді
і тільки тоді, коли
тоді
і тільки тоді, коли ![]()
![]() (нерівність
трикутника)
(нерівність
трикутника)
![]()
![]()
Кут
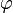 такий,
що:
такий,
що: 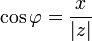 і
і 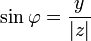 ,
називається аргументом
.
Для комплексного нуля значення аргумента
не визначене, для ненульового
числа
аргумент
визначається з точністю до
,
називається аргументом
.
Для комплексного нуля значення аргумента
не визначене, для ненульового
числа
аргумент
визначається з точністю до 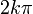 ,
де
,
де  —
будь-яке ціле
число.
—
будь-яке ціле
число.
10.
Комплексне число можна ототожнити з точкою площини:
в декартовій системі координат точка описується парою координат
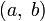 чи
чи 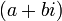 (алгебраїчна
форма комплексного числа).
(алгебраїчна
форма комплексного числа).в полярній системі координат точка описується довжиною вектора
 (від початку
координат до
даної точки) та кутом
між
віссюабсцис та
даним вектором (тригонометрична форма
комплексного числа).
(від початку
координат до
даної точки) та кутом
між
віссюабсцис та
даним вектором (тригонометрична форма
комплексного числа).
Для переходу від однієї форми запису комплексного числа до іншої користуються формулою:
![]() ,
,
де і — дійсні числа, причому додатне. У такій формі можна подати довільне комплексне число, відмінне від 0.
(називається
модулем числа
) —
це відстань між
точкою ![]() та
початком координат.
та
початком координат.
(називається аргументом числа ) — кут (виражений у радіанах) між правою піввіссю осі абсцис і вищезгаданим вектором, причому кут відраховується проти годинникової стрілки (а в разі руху за стрілкою годинника береться зі знаком «мінус»).
![]() ,
,
![]() ,
,
![]() ,
,
![]()
Геометричне представлення зручне для інтерпретації операцій над комплексними числами. Так, додавання та віднімання комплексних чисел рівносильне відповідно додаванню та відніманню відповідних векторів. При множенні комплексних чисел їх модулі множаться, а аргументи додаються (так що поворот навколо початку координат можна інтерпретувати як множення на певне комплексне число з одиничним модулем). При діленні комплексних чисел їх модулі діляться, а аргументи віднімаються. При піднесенні комплексного числа до цілого степеня його модуль підноситься по цього ж степеня, а аргумент множиться на показник степеня; це правило називається формулою Муавра і значно спрощує виконання піднесення комплексних чисел до великих степенів.
11.
тригонометрична форма комплексного числа
в полярній системі координат точка описується довжиною вектора (від початку координат до даної точки) та кутом між віссюабсцис та даним вектором (тригонометрична форма комплексного числа).
П![]() одання
числа у тригонометричній формі єдине
з точністю до цілої кількості повних
обертів, які можна додавати до аргументу.
одання
числа у тригонометричній формі єдине
з точністю до цілої кількості повних
обертів, які можна додавати до аргументу.
З використанням формули формули Ейлера можна переписати тригонометричну форму так:
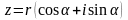 - тригонометрична
форма комплексного числа.
- тригонометрична
форма комплексного числа.
Формула Муавра — формула, за якою для будь-якого комплексного числа та будь-якого цілого числа виконується рівність:
![]()
Важливість формули полягає у поєднанні двох розділів математики — тригонометрії та комплексного аналізу.
12.
Означення.
Визначником другого порядку
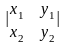 називається
число
=x1y2–y1x2
називається
число
=x1y2–y1x2
Визначником
третього порядку
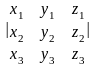 називається число
=x1y2z3+y1z2x3+z1x2y3–z1y2x3–y1x2z3–
x1z2y3
називається число
=x1y2z3+y1z2x3+z1x2y3–z1y2x3–y1x2z3–
x1z2y3
У
визначнику можна визначити дві діагоналі.
Головну діагональ визначника
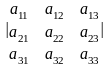 утворюють
елементи а11,
а22,
а33.
Побічну діагональ цього визначника
складають елементи а13,
а22,
а31.
утворюють
елементи а11,
а22,
а33.
Побічну діагональ цього визначника
складають елементи а13,
а22,
а31.
Для обчислення визначника третього порядку існує правило трикутників. Визначник є сумою 6-и добутків, з яких три беруться зі знаком „+” і три – зі знаком „–”.
Властиості:
Якщо один з рядків (стовпчиків) матриці помножити на число , то визначник матриці також помножиться
Якщо поміняти місцями два рядки (стовпчики), то визначник змінить знак на протилежний.
Визначник, що містить два однакові рядки (стовпчики), дорівнює нулю.
Визначник не змінюється, якщо до одного з рядків (стовпчиків) матриці додати інший рядок (стовпчик) цієї матриці.
Якщо один з рядків (стовпчиків) складається з нулів, то визначник дорівнює нулю.
Визначник матриці трикутного вигляду дорівнює добутку елементів, що знаходяться на головній діагоналі.
Якщо який-небудь рядок (стовпчик) матриці є лінійною комбінацією інших рядків (стовпчиків), то визначник дорівнює нулю.
13.
Система координат — спосіб задання точок простору за допомогою чисел. Кількість чисел, необхідних для однозначного визначення будь-якої точки простору, визначає його вимірність. Обов'язковим елементом системи координат є початок координат - точка, від якої ведеться відлік відстаней. Іншим обов'язковим елементом є одиниця довжини, яка дозволяє відраховувати відстані. Всі точки одновимірного простору можна задати при обраному початку координат одним числом. Для двовимірного простору необхідні два числа, для тривимірного - три. Ці числа називаються координатами.
двовимірна система
Сучасна Декартова система координат в двох вимірах (також знана під назвою прямокутна система координат) задається двома осями, розташованими під прямим кутом одна до одної. Площину, в якій знаходяться осі, називають іноді xy-площиною. Горизонтальна вісь позначається як x (вісь абсцис), вертикальна як y (вісь ординат). В тривимірному просторі до цих двох додається третя вісь, перпендикулярна xy-площині — вісь z. Всі точки в системі Декартових координат, складають так званийДекартовий простір.
Точка перетину, де осі зустрічаються, називається початком координат та позначається як O. Відповідно, вісь x може бути позначена як Ox, а вісь y — як Oy. Прямі, проведені паралельно до кожної осі на відстані одиничного відрізку (одиниці виміру довжини) починаючи з початку координат, формують координатну сітку. Точка в двовимірній системі координат задається двома числами
Тривимірна та n-вимірна система координат
Координати в тривимірному просторі формують трійку (x, y, z).
Координати x, y, z для тривимірної Декартової системи можна розуміти як відстані від точки до відповідних площин: yz, xz, та xy.
Тривимірна Декартова система координат є дуже популярною, тому що відповідає звичним уявам про просторові виміри — висоту, ширину та довжину (тобто три виміри). Але залежно від галузі застосування та особливостей матиматичного апарату, сенс цих трьох осей може бути зовсім іншим.
Системи координат вищих розмірностей також застосовуються (наприклад, 4-вимірна система для зображення простору-часу в спеціальній теорії відносності).
Система декартових координат у абстрактному n-вимірному просторі є узагальненням викладених вище положень та має n осей (по кожній на вимір), що є взаємоперпендикулярні. Відповідно, положення точки в такому просторі буде визначатися кортежем з n координат, або n-кою.
14.
Вектор -
це величина, яка характеризується
числовим значенням і напрямком. Під
направленим відрізком ![]() розуміють
впорядковану пару точок, перша з яких
- точка A -
називається його початком,
а друга - B -
його кінцем.
В геометрії розглядають вектори, що не
залежать від точки прикладання (вільні
вектори).
розуміють
впорядковану пару точок, перша з яких
- точка A -
називається його початком,
а друга - B -
його кінцем.
В геометрії розглядають вектори, що не
залежать від точки прикладання (вільні
вектори).
Вектори позначають двома способами:
малими буквами латинського алфавіту (наприклад,
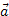 );
);двома великими буквами латинського алфавіту (наприклад, ), де перша буква - початок вектора, а друга - кінець.
Графічно вектори зображають у вигляді направлених відрізків певної довжини .
