
- •3.3 Настройка параметров типовых законов регулирования с использованием динамической модели объекта управления
- •3.4. Имитационное моделирование систем управления
- •3.5. Многоуровневое управление технологическими процессами на основе адаптивных моделей.
- •4. Идентификация статических моделей объектов управления.
- •4.1. Общая схема постановки и решения задач статистической идентификации.
- •4.2. Расчет параметров модели по методу наименьших квадратов (мнк).
- •4.3. Линейные и квадратичные по входам мнк – модели
- •4.4. Приведение моделей к линейным по параметрам
- •4.5. Вероятностная трактовка метода наименьших квадратов
- •4.6. Точность оценок по мнк
- •4.7. Проверка значимости оценок параметров регрессии
- •4.8. Оценка качества регрессионной модели
- •4.9. Влияние входных воздействий на качество регрессионных моделей
4.4. Приведение моделей к линейным по параметрам
Стандартным способом приведения нелинейных моделей к линейным по параметрам является разложение в ряд Тейлора, как правило, с точностью до первого (линейные по х модели (4.15), (4.16)) или до второго (квадратичные по х модели (4.17), (4.18)) порядка малости

![]()
или

![]()
где
![]()
Поскольку
такая аппроксимация нелинейных
зависимостей приводит к заведомо
приближённым моделям, то при возможности
следует использовать особые приёмы
линеаризации по параметрам, не связанные
с потерей![]() точности.
точности.
Пусть,
например, необходимо определить параметры
c,
d
зависимости
![]() .
Тогда,
логарифмируя, получим:
.
Тогда,
логарифмируя, получим:
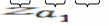
![]()
После
того, как найдём коэффициенты ![]() линейной по параметрам модели из условия
минимизации
линейной по параметрам модели из условия
минимизации ![]() определим исходные параметры
определим исходные параметры ![]() .
.
Приведём несколько других примеров, сведя их в таблицу.
Исходная функция |
Преобразованная функция |
|
|
|
|
|
|
|
|
Приведём содержательный пример, относящийся к химической технологии. Уравнение Аррениуса, определяющее кинетику химичнских реакций, имеет вид
![]() (4.26)
(4.26)
где
К
– константа скорости реакции, Т
– температура
в ![]() ,
Е
– энергия активации, R
– универсальная газовая постоянная,
известная из теории.
,
Е
– энергия активации, R
– универсальная газовая постоянная,
известная из теории.
Здесь
выходом модели является К,
входом - Т,
а параметры ![]() и Е
подлежат
определению.
и Е
подлежат
определению.
Модель нелинейная по параметру Е, так что непосредственно МНК в линейном по параметрам варианте неприменим. Прологарифмируем обе части (4.26).
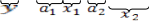
![]()
Обозначая
![]()
приходим к стандартной модели
![]()
определив
параметры которой ![]() по МНК, найдём параметры исходной модели
(4.26)
по МНК, найдём параметры исходной модели
(4.26)
![]()
4.5. Вероятностная трактовка метода наименьших квадратов
Популярность МНК связана не только с простотой расчёта параметров моделей, но и с возможностью его вероятностного обоснования как, при определённых условиях, наилучшего метода определения параметров. Подобное обоснование позволяет также оценить точность получаемых моделей.
В
вероятностной трактовке МНК предполагается,
что существует зависимость между![]() и
и ![]() вида
вида ![]() ,
отражающая связь между
и
,
отражающая связь между
и ![]() лишь в среднем или, более конкретно,
лишь в среднем или, более конкретно,
![]() ,
т.е. зависимость
,
т.е. зависимость ![]() представляет собой условное математическое
ожидание выхода модели
при значениях входов
представляет собой условное математическое
ожидание выхода модели
при значениях входов ![]() .
В отличие от функциональных зависимостей
такие зависимости называются
регрессионными. Задача МНК при этом
заключается в нахождении оценок
параметров а
регрессионных
моделей.
.
В отличие от функциональных зависимостей
такие зависимости называются
регрессионными. Задача МНК при этом
заключается в нахождении оценок
параметров а
регрессионных
моделей.
…(47), существуют два основных источника неточностей экспериментально-статистических моделей, проявляющихся в том, что
![]() (4.27)
(4.27)
Искажение формы истинной зависимости. Оно, например, происходит из-за неполной достоверности гипотез, принятых для описания моделируемых явлений. Так, при отсутствии точных представлений о гладкости идентифицируемых зависимостей, приближая их линейной формой или формой второго порядка, что, разумеется, сопряжено с погрешностями.
Факторы неопределённости в результатах измерений. Имеется два основных источника неопределённости:
Случайные ошибки измерений;
Наличие неучтённых или (и) неконтролируемых факторов, влияющих случайным образом на y помимо x.
Допущения, которые кладутся в основу вероятностного обоснования МНК, предполагают отсутствие искажения формы модельной (регрессионной) зависимости, т.е. предполагается, что существуют значения параметров а, называемые истинными, такие, что при отсутствии факторов неопределённости зависимость точно описывает функциональную связь между x и y для всех наблюдаемых значений x.
Кроме
того, делается ряд допущений относительно
случайных отклонений
экспериментальных данных
от истинных значений ![]() ,
а именно:
считается независимыми (для разных i)
нормально распределёнными случайными
величинами с нулевым мат ожиданием и
одинаковыми i
хотя, как правило, заранее не известными,
дисперсиями
,
а именно:
считается независимыми (для разных i)
нормально распределёнными случайными
величинами с нулевым мат ожиданием и
одинаковыми i
хотя, как правило, заранее не известными,
дисперсиями ![]() .
.
При выполнении этих допущений МНК – оценки, а обладает следующими важными свойствами:
Несмещённость, т.е.
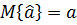 (при любом конечном N
оценка МНК не даёт систематического
сдвига оценок по отношению к истинным
значениям параметров модели);
(при любом конечном N
оценка МНК не даёт систематического
сдвига оценок по отношению к истинным
значениям параметров модели);Состоятельность, т.е.
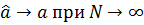 (т.е. оценки МНК сходятся к истинным
значениям параметров модели при
увеличении числа наблюдений
/экспериментов/).
(т.е. оценки МНК сходятся к истинным
значениям параметров модели при
увеличении числа наблюдений
/экспериментов/).
Здесь
необходимы пояснения. Рассмотрим
корреляционную матрицу оценок ![]() ,
являющуюся мерой отклонения оценок от
истинных значений параметров (диагональные
элементы этой матрицы).
,
являющуюся мерой отклонения оценок от
истинных значений параметров (диагональные
элементы этой матрицы).
![]() (4.27)
(4.27)
Равны
дисперсиям /или квадратам СКО/ отклонений
![]() .
.
Тогда можно показать, что
![]() ,
(4.28)
,
(4.28)
Если допустить, что существует
![]() ,
(4.29)
,
(4.29)
То
![]() (4.30)
(4.30)
а
значит ![]() (4.31)
(4.31)
В частности, отсюда следует, что
![]() (4.32)
(4.32)
где
![]()
и
что ![]() (4.33)
(4.33)
Эффективность, т.е. МНК – оценки точнее всех других оценок параметров (при сделанных допущениях: нормальное распределение и взаимная независимость измерительных ошибок , отсутствие априорной информации об оцениваемых параметрах). Более конкретно,
(МНК) (Любой другой способ оценивания)
![]() (4.34)
(4.34)
