Вопрос 9

Включение конденсатора в цепь переменного тока не вызывает разрыва цепи, так как ток в цепи все время поддерживается за счет заряда и разряда конденсатора. Пусть напряжение (рис. 2.8 а)

,тогда

   (2.17)

Формула (2.17) показывает, что ток опережает приложенное напряжение на угол   . Нулевым значениям тока соответствуют максимальные значения напряжения. Физически это объясняется тем, что при достижении электрическим зарядом и соответственно напряжением максимального значения ток становится равным нулю.

Под фазовым сдвигом тока относительно напряжения здесь, как и раньше, подразумевается разность начальных фаз напряжения и тока, т.е.

.

Таким образом, в отличие от цепи с катушкой, где  , угол сдвига фаз в цепи с конденсатором отрицателен.

 Из (2.17) видно, что амплитуды тока и напряжения связаны законом Ома

, где  – емкостное сопротивление, имеющее размерность Ом.

Мгновенная мощность, поступающая в конденсатор

, 

колеблется синусоидально с угловой частотой 2 , имея амплитуду, равную   (рис. 2.8 г). Поступая от источника, энергия временно запасается в электрическом поле конденсатора, затем возвращается источнику при исчезновении электрического поля. Таким образом, здесь, как и в цепи с катушкой, происходит колебание энергии между источником и конденсатором, причем активная мощность   = 0. Амплитуду колебания мощности в цепи с конденсатором называют реактивной (емкостной) мощностью

.

Зависимость ЭДС генератора от тока возбуждения называется характеристикой холостого хода E = Uхх = f (Iв).  Характеристику холостого хода получают при разомкнутой внешней цепи (Iя) и при постоянной частоте вращения (n2 = const)  Характеристика холостого хода генератора показана на рис. 11.8.  Из-за остаточного магнитного потока ЭДС генератора не равна нулю при токе возбуждения, равном нулю.  При увеличении тока возбуждения ЭДС генератора сначала возрастает пропорционально.  Соответствующая часть характеристики холостого хода будет прямолинейна. Но при дальнейшем увеличении тока возбуждения происходит магнитное насыщение машины, отчего кривая будет иметь изгиб. При последующем возрастании тока возбуждения ЭДС генератора почти не меняется. Если уменьшать ток возбуждения, кривая размагничивания не совпадает с кривой намагничивания из-за явления гистерезиса.  Зависимость напряжения на внешних зажимах машины от величины тока нагрузки U = f (I) при токе возбуждения Iв = const называют внешней характеристикой генератора. 

Вопрос 10

Множитель  в уравнении (3.30) представляет собой комплекс, имеет размерность сопротивления и обозначается через Z. Его называют комплексным сопротивлением:

Как и всякий комплекс, Z можно записать в показательной форме. Модуль комплексного сопротивления принято обозначать через z. Точку над Z не ставят, потому что принято ставить ее только над такими комплексными величинами, которые отображают синусоидальные функции времени.

Уравнение (3.30) можно записать так:  Разделим обе его части на и перейдем от комплексных амплитуд к комплексам действующих значений и Е:

Уравнение (3.30) представляет собой закон Ома для цепи синусоидального тока.

В общем случае Z имеет некоторую действительную часть R и некоторую мнимую часть

где R — активное сопротивление; X — реактивное сопротивление. Для схемы (см. рис. 3.9) реактивное сопротивление

Активное сопротивление (резистивный элемент – рис. 2.7).

для мгновенных значений напряжения и тока справедливо соотношение: где

или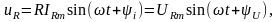

где амплитуды тока и напряжения связаны выражением (2.7)

а их начальные фазы одинаковы: 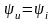(2.8)

Ток и напряжение в активном сопротивлении изменяются синфазно, т.е. совпадают по фазе. (см. рис. 2.7.а).

Разделив (2.7) на получим соотношения для действующих значений U и I или закон Ома в комплексном виде для активного сопротивления (резистивного элемента R): 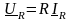(2.9) Действующие значения синусоидальных напряжений и токов связаны между собой законом Ома так же как постоянные напряжения и ток.

Комплексной проводимостью называется отношение комплексного тока к комплексному напряжению : Y=I/U=1/Z=1/(zejj)=ye‑jj=yÐ‑j,  (6.31а)

где y=1/z — величина, обратная полному сопротивлению, называется полной проводимостью.

Комплексная проводимость и комплексное сопротивление взаимно обратны. Комплексную проводимость можно представить в виде

 Y= ye‑jj=ycosj‑jysinj=g‑jb, (6.31б) 

 где g=ycosj — действительная часть комплексной проводимости, называется активной проводимостью; b=ysinj — значение мнимой части комплексной проводимости, называется реактивной проводимостью;

  .(6.32)

 Из (6.30) и (6.29) следует, что для схемы, представленной на рис. 6.12, комплексная проводимость

 Y=1/r‑j[1/(wL)‑wC]=g‑j(bL‑bC), где g=1/r;  bL=1/(wL)=1/xL; bC=wC=1/xС

 и называются соответственно активной, индуктивной и емкостной проводимостями.

Реактивная проводимость

 b=bL‑bC.  (6.33)