Билет 1
1.Метод узловых потенциалов. Определение числа независимых уравнений. Матричная запись системы уравнений. Полная матрица узлов (матрица инциденций). Примеры.
Метод узловых напряжений (потенциалов) заключается в том, что на основании первого закона Кирхгофа определяются напряжения в узлах электрической цепи относительно некоторого базисного узла. Эти искомые напряжения называются узловыми напряжениями. Зная узловые напряжения в электрической цепи можно найти токи в ветвях.
Запишем 1-й закон Кирхгофа для всех независимых узлов: 1/(jωc1)+1/(jωc2)=1/(jωcэ), где сэ - эквивалентная емкость. сэ=(с1*с2)/(с1+с2)
q – узлов, p – ветвей, Nн – идеальных источников напряжений.
Число независимых уравнений: Ny=q-1-NH. Либо с помощью Графа и его дерева, по количеству ветвей графа определяем количество не зависимых уравнений.
Полная
матрица узлов
(используются также другие названия
этой матрицы: полная
матрица инциденций,
матрица
соединений,
структурная
матрица)
– это таблица, в которой число столбцов
равно числу ветвей графа p,
а число строк равно числу узлов q.
Номера строк совпадают с номерами узлов
(строка с нулевым номером обычно
располагается последней), номера
столбцов совпадают с номерами ветвей.
Элемент матрицы aij,
расположенный на пересечении i-й
строки и j-го
столбца, может принимать значения +1,
-1 и 0: aij
= +1, если ветвь j
инцидентна узлу i
и направлена от этого узла; aij
= -1, если ветвь j
инцидентна узлу i
и направлена к этому узлу; aij
= 0, если ветвь j
не инцидентна узлу i.
В соответствии с первым
законом Кирхгофа окончательно имеем
Матричная
запись системы уравнений.
,
,
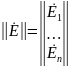это
вид матриц. Уравнение имеет вид
2. Понятие о комплексных частотных характеристиках(кчх). Амплитудно-частотоные характеристики(ачх), фазо-частотные характеристики(фчх), годограф цепи.
Задача анализа электрической цепи была сформулирована ранее как задача определения реакции цепи на заданное внешнее воздействие. Вынесем из рассматриваемой цепи все ветви, содержащие независимые источники тока и напряжения, а также ветви, токи или напряжения которых подлежат определению. Оставшуюся часть цепи, содержащую идеализированные пассивные элементы и управляемые источники, представим в виде многополюсника
З
ажимы
(полюса), к кот. подкл. кажд. из независим.
и сточ., задающих внеш. воздействие на цепь, наз.
в
ходными.
зажимы,
служащие для подкл. нагрузки, т.е ветви,
I или U кот. необход. опред., наз. выходными. Пара зажимов
наз. так же портом или стороной многополюсника.
Особенности:
1) ток, втекающий через один зажим порта, равен I, вытек.
вытекающему через другой зажим этого же порта;
2) между парами полюсов, принадлежащих к разным портам, не должно быть никаких внешних по отношению к многополиснику соединений (внутри многополюсника соединения, естественно могут быть).
Комплексной частотной характеристикой цепи называется отношение комплексных изображений отклика и воздействия: Hkv(jω)=Ymk/Xmv=Yk/Xv, где Ymk, Yk — комплексные амплитуда и действующее значение реакции цепи; Xmk, Xk — комплексные амплитуда и действующее значение внешнего воздействия; k — номер выходных зажимов; v — номер входных зажимов.
В зависимости от того, какие величины (токи или напряжения) рассматриваются в качестве откликов и внешних воздействий, КЧХ. может иметь размерность сопротивления, проводимости или быть безразмерной.
КЧХ цепи численно равна комплексной амплитуде реакции цепи на внешнее воздействие с единичной амплитудой и нулевой начальной фазой.
Зависимости модуля Нkv (ω) и аргумента ψkv (ω) комплексной частотной характеристики от частоты со называются амплитудно-частотной (АЧХ) и фазо-частотной (ФЧХ) характеристиками цепи.
Комплексную частотную характеристику можно изобразить и в виде одной зависимости— годографа КЧХ, построенного на комплексной плоскости. Годограф КЧХ представляет собой геометрическое место концов вектора Hkv(jω), соответствующих изменению частоты от ω=0 до ω=∞. На годографе указываются точки, соответствующим некоторым значением частоты ω, и стрелкой показывают направление перемещения конца вектора Hkv(jω) при увеличении частоты. КЧХ линейных цепей не зависят от амплитуды и начальной фазы внешнего воздействия, а определяются структурой цепи и параметрами входящих в нее элементов. Знание КЧХ позволяет определить реакцию цепи на заданное гармоническое воздействие.
Билет 2