Свойства непрерывных функций

Теорема. Если f(x) и g(x) непрерывны в точке x₀, то в этой же точке непрерывны и функции f(x)  g(x), f(x)  g(x) и f(x)/g(x) (последнее только в случае, если g(x₀)0).

Определение. Пусть y = f(x) и x = (t). Тогда комбинация y = f((t)) называется суперпозицией функций f(x) и (t), или сложной функцией.

Теорема о непрерывности сложной функции.

Пусть x = (t) непрерывна в точке t₀, а функция f(x) непрерывна в точке     x₀ = (t₀). Тогда функция y = f((t)) непрерывна в точке t₀.

Короче говоря, суперпозиция непрерывных функций есть также непрерывная функция.

Непрерывность элементарных функций

Все элементарные функции являются непрерывными в любой точке свой области определения.  Функция называется элементарной, если она построена из конечного числа композиций и комбинаций  (с использованием 4 действий - сложение, вычитание, умножение и деление) основных элементарных функций. Множество основных элементарных функций включает в себя:

1. Алгебраические многочлены  ;

2. Рациональные дроби  ;

3. Степенные функции  ;

4. Показательные функции  ;

5. Логарифмические функции  ;

6. Тригонометрические функции  ;

7. Обратные тригонометрические функции  ;

8. Гиперболические функции  ;

9. Обратные гиперболические функции  .

17.

Односторо́нний преде́л в математическом анализе — предел числовой функции, подразумевающий «приближение» к предельной точке с одной стороны. Такие пределы называют соответственно левосторо́нним преде́лом (или преде́лом сле́ва) и правосторо́нним преде́лом (преде́лом спра́ва).

• Правосторонний предел принято обозначать любым из нижеследующих способов:

• Аналогичным образом для левосторонних пределов приняты обозначения:

• При этом используются также сокращённые обозначения:

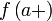  •  и   для правого предела;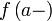

  •  и 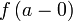  для левого предела.

Классификация точек разрыва функции

Все точки разрыва функции разделяются на точки разрыва первого и второго рода.  Говорят, что функция f (x) имеет точку разрыва первого рода при x = a, если в это точке

• Существуют левосторонний предел   и правосторонний предел  ;

• Эти односторонние пределы конечны.

При этом возможно следующие два случая:

• Левосторонний предел и правосторонний предел равны друг другу:

Такая точка называется точкой устранимого разрыва.

• Левосторонний предел и правосторонний предел не равны друг другу:

Такая точка называется точкой конечного разрыва. Модуль разности значений односторонних пределов  называется скачком функции.

Функция f (x) имеет точку разрыва второго рода при x = a, если по крайней мере один из односторонних пределов не существует или равен бесконечности. 

18.

Основной тригонометрический предел (первый замечательный предел) имеет вид

Используя данный предел, можно получить ряд других тригонометрических пределов:

      

Здесь и далее предполагается, что углы измеряются в радианах. 

Замеча́тельные преде́лы — термин, использующийся в советских и российских учебниках по математическому анализу для обозначения некоторых широко известных математических тождеств со взятием предела. Особенно известны:

Первый замечательный предел

Доказательство

Рассмотрим два односторонних предела и и докажем, что каждый из них равен 1. Тогда двусторонний предел также будет равняться 1.

Итак, пусть (этот интервал -- одно из окончаний базы ). В тригонометрическом круге (радиуса ) с центром построим центральный угол, равный , и проведём вертикальную касательную в точке пересечения горизонтальной оси с окружностью (). Обозначим точку пересечения луча с углом наклона с окружностью буквой , а с вертикальной касательной -- буквой ; через обозначим проекцию точки на горизонтальную ось.

19.

Натуральный логарифм — это логарифм по основанию e, где e — иррациональная константа, равная приблизительно 2,718281828. Натуральный логарифм обычно обозначают как ln(x), log_e(x) или иногда просто log(x), если основание e подразумевается.^[1]

Натуральный логарифм числа x (записывается как ln(x)) — это показатель степени, в которую нужно возвести число e, чтобы получить x. Например, ln(7,389...) равен 2, потому что e²=7,389.... Натуральный логарифм самого числа e (ln(e)) равен 1, потому что e¹ = e, а натуральный логарифм 1 (ln(1)) равен 0, поскольку e⁰ = 1.

Натуральный логарифм может быть определён для любого положительного вещественного числа a как площадь под кривой y = 1/x от 1 до a. Простота этого определения, которое согласуется со многими другими формулами, в которых применяется натуральный логарифм, привела к появлению названия «натуральный». Это определение можно расширить на комплексные числа, о чём будет сказано ниже.

Если рассматривать натуральный логарифм как вещественную функцию действительной переменной, то она является обратной функцией к экспоненциальной функции, что приводит к тождествам:

Подобно всем логарифмам, натуральный логарифм отображает умножение в сложение:

Таким образом, логарифмическая функция представляет собой изоморфизм группы положительных действительных чисел относительно умножения на группу вещественных чисел по сложению, который можно представить в виде функции:

Логарифм может быть определён для любого положительного основания, отличного от 1, а не только для e, но логарифмы для других оснований отличаются от натурального логарифма только постоянным множителем, и, как правило, определяются в терминах натурального логарифма. Логарифмы полезны для решения уравнений, в которых неизвестные присутствуют в качестве показателя степени. Например, логарифмы используются для нахождения постоянной распада для известного периода полураспада, или для нахождения времени распада в решении проблем радиоактивности. Они играют важную роль во многих областях математики и прикладных наук, применяются в сфере финансов для решения многих задач, включая нахождение сложных процентов.