1

1. Понятие матрицы. Линейные операции над матрицами. Произведение и транспонированием матриц.

1⁰. Понятие матрицы.

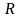
Прямоугольная таблица чисел из множества или других однородных элементов называется матрицей. Символом обозначено множество действительных чисел. Для записи матрицы используют ( ),также квадратные скобки или двойные черты .

Числа , называются элементами матрицы.

Матрицы обозначаются латинскими буквами A, B, C, D,… .

Для обозначения матрицы используются символы

Если матрицы имеют m строк и n столбцов, то говорят, что матрица имеет размерность .

Матрица A квадратная, если .

Главная диагональ ,

побочная диагональ .

Если все элементы квадратной матрицы, за исключением элементов главной диагонали равны 0, то матрица называется диагональной.

Матрица диагональная.

Если , то диагональная матрица называется единичной и обозначается (или ).

Матрицы A и B называются равными , если они имеют одинаковые размерности и их соответствующие элементы равны .

─ матрица-столбец, ─ матрица-строка.

1¹. Линейные операции над матрицами.

Линейными операциями над матрицами называются сложение и вычитание матриц, умножение матриц на число. 

1.Суммой A+B двух матриц и одинаковых размерностей называется матрица той же размерности, каждый элемент которой равен сумме соответствующих элементов матриц A и B:

.

Свойства сложения

1. ,

2. ,

где A, B, C – произвольные матрицы одинаковых размеров.

2.Произведением матрицы на число называется матрица , каждый элемент которой есть произведение соответствующего элемента матрицы A и числа : , т.е.

.

Пример

.

Свойства

1. ,

2. ,

3. .

Здесь – матрицы одинаковых размерностей, а – действительные числа.

3.Разностью двух матриц и одинаковых размерностей назовем матрицу такой же размерности, которая определяется по правилу

.

Из определений следует, что , .

1².Произведение и транспонированием матриц.

Произведением двух матриц А и В, где матрица А имеет размерность mхn, а матрица В имеет размерность nxp, называется матрица С mxp, каждый элемент которой равен сумме произведений элементов i-той строки матрицы А на соответствующий элемент j-го столбца матрицы B:

, .

Пример:

Отметим, что операция умножения двух матриц выполнима тогда и только тогда, когда число столбцов в первом сомножителе равно числу строк во втором.

Свойства

1. ,

2. ,

3. .

Операция умножения матриц не обладает переместительным (коммутативным) свойством. (АВ≠ВА)

Пример.

.

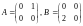
Если , то матрицы и называются перестановочными или коммутирующими между собой.

Пример.

, .

, .

Матрица размерности называется транспонированной к матрице A размерности , если она получена путем замены строк матрицы A столбцами этой же матрицы с теми же номерами:

.

Свойства:

1. ,

2. ,

3. ,

4. .

2. Определители 2 и 3-го порядков. Вычисление определителя n-го порядка. Свойства определителей 3-го порядка.

2¹. Определители 2 и 3-го порядков.

Каждой квадратной матрице А можно поставить в соответствие число, которое называется ее определителем.

Для обозначения определителя используются символы , .

Определителем первого порядка матрицы называют число .

Определителем второго порядка матрицы называется число ,определяемое по правилам .

Для матрицы определителем третьего порядка назовем число, определяемое равенством:

.

Раскрывая последнюю формулу, получим, что определитель третьего порядка можно вычислить по формуле:

2². Вычисление определителя n-го порядка.

Определитель порядка , который получается из матрицы A в результате вычеркивания i-ой строки и j-го столбца, называется минором элемента .

Определителем порядка n, называется число вычисляемое по правилам:

= (1)

=а₁₁М₁₁ - а₁₂М₁₂ + а₁₃М₁₃ + … + (-1)¹⁺ⁿ а_1nМ_1n

Формула (1) называется разложением определителя по элементам первой строки. При равенство (1) равносильно определению определителя второго порядка, а при ─ определению определителя третьего порядка.

В частности, определитель четвертого порядка, соответствующий матрице

,

определяется равенством:

Наряду с формулой (1) для каждого определителя матрицы A порядка , имеет место разложение по первому столбцу:

.

2³. Свойства определителей 3-го порядка.

1) При транспонировании матрицы ее определитель 3-го порядка не меняется:

.

Доказательство.

 

 

=

2) При перестановке двух строк или двух столбцов знак определителя 3-го порядка меняется на противоположный.

Доказательство. Пусть в матрице третьего порядка перестановлены первая и третья строки. Покажем, что

(3)

Разлагая определитель, стоящий в левой части равенства (3), по элементам первой строки, получим

Разлагая же определитель, стоящий в правой части этого равенства, по элементам третьей строки, получим

т.е. то же выражение, но с противоположным знаком.

3) Если определитель 3-го порядка имеет два одинаковых столбца или две одинаковых строки, то он равен нулю.

Доказательство.

4) Общий множитель всех элементов одного столбца или одной строки можно вынести за знак определителя 3-го порядка.

Доказательство.

 

         

Это свойство иногда формулируют так: общий множитель всех элементов строки можно выносить за знак определителя.

5) Если все элементы некоторого столбца или некоторой строки равны нулю, то и сам определитель 3-го порядка равен нулю.

Доказательство этого свойства следует из свойства 4 при k = 0.

6) Если элементы двух столбцов или двух строк определителя 3-го порядка пропорциональны, то определитель равен нулю.

Доказательство. Пусть, например, элементы третьей строки пропорциональны элементам первой, т.е.