
- •1.Вплив часу на параметри моделі Самуельсона - Хікса.
- •2.Моделі дискретної економічної динаміки.
- •3.Які системи вивчаються в теорії катастроф?
- •4.Модель рівноваги Вальраса.
- •5.B чому сутність моделі валютної паніки?
- •6.Які висновки можна зробити за моделями?
- •7.З чого складається властивість стійкості системи?
- •8.Дискретна й безперервна моделі попиту та пропозиції.
- •9.Моделі динаміки суспільного продукту і національного доходу.
- •12.Які існують види фракталів?
- •11.Поняття про стабільність лінійних систем.
- •13.Розв’язування диференційних рівнянь макроекономічної динаміки.
- •14.Які типи катастроф існують у двовимірному випадку?
- •15.Стабільність і рівновага в динамічних системах.
- •16.Розходження в поводженні моделі в. Леонтьєва при зміні структурних коефіцієнтів моделі.
- •17.Опишіть зміни капіталовкладень й інших показників у різних варіантах моделі Гудвіна.
- •18.Основні положення моделі Харрода - Домара.
- •19.Що є джерелом хаотичного поводження системи?
- •22.Що затверджує теорема Ляпунова про стійкість?
- •23.Які методи застосовуються для виявлення хаотичного поводження?
- •20.B чому відмінність поняття стійкості для стохастичних систем?
- •25.Який зв'язок фракталів і хаосу?
- •21.Проведіть аналіз дисипативних систем для макроекономіки.
- •24.B чому розходження й спільність підходів ідей різних шкіл?
- •26.B чому суть модифікацій моделей економічних циклів Гудвіна?
- •27.Які випадкові процеси називаються стійкими?
- •28.Що являють собою вузол, сідло, фокус, центр?
- •29.Які основні якісні характеристики складної системи? Дайте коротке пояснення кожній властивості.
- •31.B чому полягає розходження поводження й розвитку системи?
- •30.Яким чином ураховуються виробничі цикли в моделях динаміки корисності споживчих благ?
- •32.У чому полягає основне завдання якісного аналізу динамічних систем?
- •33.Сформулюйте основні положення синергетики.
- •34.B чому відмінність хаотичного поводження від випадкового?
- •35.Яка система називається динамічною? Якими складовими формально описується динамічна система?
- •36.Які виділяються типи стійкості стану системи?
- •37.Методи розв'язання дискретної й безперервної моделі попиту та пропозиції.
- •38.Поняття про допустимість стану й траєкторії моделі в. Леонтьєва.
- •42.Взаємозв’язок акселератора з мультиплікатором.
- •39.Типи поведінки економічної системи.
- •40.Ha яких рівняннях заснована дана модель?
- •43.Що мається на увазі під біфуркацією?
- •41.Які виділяються види диференціальних рівнянь 1-го порядку?
- •44.B чому суть моделі, запропонованої в. С. Михалевичем?
- •45.Які методи можна застосувати для управління хаотичними системами? b чому їхні переваги й недоліки?
- •46.Критерії та умови оптимізації.
- •47.Розв’язування задач оптимального управління.
- •53.B чому сутність технологічної концепції суспільної еволюції?
- •48.Стійкість загальної рівноваги Вальраса.
- •49.Ha яких економічних законах засновані ефекти, отримані в моделі динаміки корисності споживчих благ?
- •50.Нормальна ціна в павукоподібній моделі.
- •51.Як у даній моделі відбивається платоспроможний споживчий попит?
- •52.Характеристики швидкості та інтенсивності зміни динамічного ряду.
- •54.Рішення моделі в. Леонтьєва у випадку відсутності екзогенного споживання та його обліком.
- •55.B чому сутність стохастичних моделей економічної динаміки?
- •56.Яким образом може бути представлена потенційна функція системи при наявності катастрофи?
- •57.Для чого застосовуються фрактали в дослідженні складних систем?
- •58..Які види перетворень використовуються для опису динамічних характеристик систем?
- •59.Які причини появи синергетики і її часткових напрямів?
- •60.B чому розходження системного й синергетичного підходів до дослідження складних систем?
- •63.Які припущення використовуються в моделях економічних циклів Гудвіна?
- •61.Найпростіша динамічна модель з мультиплікатором.
- •62.Основні припущення моделі в. Леонтьєва.
- •64.У чому відмінності кількісних, структурних і якісних змін у системах?
- •67.Показники економічної динаміки.
- •65.Які явища в поводженні системи можуть указувати на наявність катастрофи?
- •66.Якою формальною моделлю можна видобразити грошові й товарні потоки?
- •68.Охарактеризуйте модель оцінки валютних потоків.
- •69.Що таке атрактори і які їх основні види?
- •70.Чим пояснюється наявність біфуркації в поводженні системи?
- •71.Модель зовнішньої торгівлі.
- •72.Що означає стійкість системи?
- •73.У чому відмінність загального й приватного розв’язання диференціального рівняння
- •74.Визначення найкращого темпу приросту споживання.
- •75.Закон збереження ресурсу й грошова форма збереження ресурсу.
- •76.Охарактеризуйте основні поняття самоорганізації?
- •78.Проінтерпретуйте поняття граничний цикл і фазові переходи.
- •79.Наведіть приклади, що описують розвиток валютної паніки?
- •80.Як ураховується нестаціонарний випадок для даної моделі?
- •81.Який вид має звичайне диференціальне рівняння? Система диференціальних рівнянь?
- •82.Проведіть аналіз розв'язань в моделях економічних циклів.
- •83.Які існують різні механізми якісних змін?
- •84.Що являє собою траєкторія поводження системи?
- •85.Що являє собою рівноважний стан системи?
- •86.Багатофакорні моделі економічного зростання
- •87.Якими факторами визначається динаміка корисності споживчих благ у зазначених моделях?
- •88.Критерій стійкості Гурвіца.
- •89.Основні показники економічної динаміки при неперервних змінах.
- •90.Якими методами в даній моделі вирішується система диференціальних рівнянь?
- •91.Проведіть аналіз моделі Самуельсона - Хікса.
- •92.Які явища називаються фракталами?
- •93.Поняття технологічного темпу приросту випуску продукції.
- •94.Наведіть приклади швидких процесів в економіці.
- •77.B чому розходження понять «рівновага», «стійкість» і «стаціонарність»?
- •95.Яким чином здіснюється якісний аналіз?
- •96.B чому проявляється катастрофа типу складка, зборка?
- •97.Як проводиться класифікація станів рівноваги для систем другого порядку?
- •98.Що являє собою функція катастрофи?
- •99.Які основні вимоги пред'являють до макромоделей і параметрів їхнього опису?
- •100.Що означає розв'язати диференціальне рівняння?
- •101.Предмет і завдання моделювання макроекономічної динаміки.
- •102.Моделі неперервних динамічних систем в економіці.
- •103,Що вивчає економічна динаміка?
- •104,Загальний вид рівнянь динамічної моделі в. Леонтьєва.
- •105,Макроекономічні динамічні виробничі функції.
- •Вплив часу на параметри моделі Самуельсона - Хікса.
- •Моделі дискретної економічної динаміки.
9.Моделі динаміки суспільного продукту і національного доходу.
Модель
відтворення суспільного продукту і
національного доходу: х - валовий
суспільний продукт; у - національний
дохід; а - матеріаломісткість валового
суспільного продукту.Допускається, що
експорт та імпорт дорівнюють один
одному (зовнішньоторговельне сальдо
дорівнює нулю), втрати включаються до
використовуваний національний дохід.
При цих умовах обсяги виробленого та
використовуваного національного доходу
рівні.
Баланс
виробництва та розподілу валового
суспільного продукту для кожного
моменту (проміжку) часу має вигляд
x
= ax
+ y
(10.1)
звідки 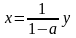 (10.2)
Коефіцієнт
- характеризує співвідношення валового
суспільного продукту і національного
доходу (або мультиплікатор валового
суспільного продукту). Динаміка
коефіцієнтів а і А може виражатися
функціями часу а = a (t), A = A (t). З урахуванням
динаміки матеріаломісткості виробництва
співвідношення між валовим суспільним
продуктом і використовуваним національним
доходом приймає видx x(t)=A(t)y(t)
(10.3)
(10.2)
Коефіцієнт
- характеризує співвідношення валового
суспільного продукту і національного
доходу (або мультиплікатор валового
суспільного продукту). Динаміка
коефіцієнтів а і А може виражатися
функціями часу а = a (t), A = A (t). З урахуванням
динаміки матеріаломісткості виробництва
співвідношення між валовим суспільним
продуктом і використовуваним національним
доходом приймає видx x(t)=A(t)y(t)
(10.3)
Найпростіша
модель.
Найбільш проста модель відтворення
національного доходу формулюється при
використанні двох припущень: а)
пропорційності виробничого накопичення
приросту національного доходу в той
же момент часу; б) незалежності (екзогенні)
динаміки споживання: 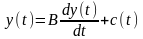 (10.5) Зростання
з постійною і монотонною змінною нормою
накопичення. Постійна
норма накопичення.
При r = р0 перший доданок в (10.9) звертається
в нуль. Темп приросту національного
доходу дорівнює темпу приросту
споживання:
(10.5) Зростання
з постійною і монотонною змінною нормою
накопичення. Постійна
норма накопичення.
При r = р0 перший доданок в (10.9) звертається
в нуль. Темп приросту національного
доходу дорівнює темпу приросту
споживання: 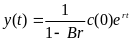 (10.10)Економічний розвиток здійснюється
з постійною нормою накопичення. Оскільки
(10.10)Економічний розвиток здійснюється
з постійною нормою накопичення. Оскільки
 і
,
то еквівалентним є рішення в більш
простому вигляді:
і
,
то еквівалентним є рішення в більш
простому вигляді: 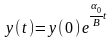 (10.11) Зменшувана
норма накопичення. При
r>
(10.11) Зменшувана
норма накопичення. При
r>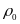 перший
доданок рішення (10.9) негативно, друге
позитивно. При цьому перший доданок по
абсолютній величині зростає швидше
другого. Внаслідок цього темп приросту
національного доходу падає, норма
накопичення зменшується до нуля, а
потім стає негативною. Подальше
збільшення норма накопичення.
При r<
перший
доданок рішення (10.9) негативно, друге
позитивно. При цьому перший доданок по
абсолютній величині зростає швидше
другого. Внаслідок цього темп приросту
національного доходу падає, норма
накопичення зменшується до нуля, а
потім стає негативною. Подальше
збільшення норма накопичення.
При r<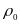 обидва
доданків у вирішенні (10.9) позитивні,
при цьому перший доданок зростає швидше
другого. Тому темп приросту національного
доходу безперервно збільшується від
в початковий момент до в межі
обидва
доданків у вирішенні (10.9) позитивні,
при цьому перший доданок зростає швидше
другого. Тому темп приросту національного
доходу безперервно збільшується від
в початковий момент до в межі .
Норма накопичення також безперервно
збільшується.Модель
із зосередженим лагом.
Позначимо величину зосередженого
лага
.
Норма накопичення також безперервно
збільшується.Модель
із зосередженим лагом.
Позначимо величину зосередженого
лага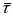 .
Тоді
.
Тоді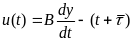 ,
а загальна модель відтворення
національного доходу набуває вигляду
,
а загальна модель відтворення
національного доходу набуває вигляду 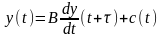 (10.12)Модель
з розподіленим лагом.
Виробниче нагромадження з розподіленим
лагом визначається за формулою
(10.12)Модель
з розподіленим лагом.
Виробниче нагромадження з розподіленим
лагом визначається за формулою 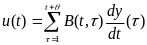 ,де
B(t,
,де
B(t,
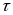 )
-
витрати капітальних вкладень в момент
t, необхідні для отримання одиниці
приросту національного доходу в момент.
)
-
витрати капітальних вкладень в момент
t, необхідні для отримання одиниці
приросту національного доходу в момент.
12.Які існують види фракталів?
Прийнято виділяти три види фракталів: геометричні, алгебраїчні й стохастичні. 1.Геометричні .Фрактали цього класу найбільш наочні. У двовимірному випадку їх отримують за допомогою деякої ламаної (або поверхні в тривимірному випадку), званої генератором. За один крок алгоритму кожен з відрізків, що складають ламану, замінюється на ламану-генератор, у відповідному масштабі. В результаті нескінченного повторення цієї процедури, виходить геометричний фрактал.
Один з таких фрактальних об'єктів - триадную криву Коха. Побудова кривої починається з відрізка одиничної довжини - це нульове покоління кривої Коха. Далі кожна ланка (в нульовому поколінні один відрізок) заміняється на утворюючий елемент. У результаті такої заміни виходить наступне покоління кривої Коха. Для отримання кожного наступного покоління всі ланки попереднього покоління необхідно замінити зменшеним утворюючим елементом. Крива n-го покоління при будь-якому кінцевому n називається предфракталом.
2) Алгебраїчні фрактали.
Це найбільша група фракталів. Отримують їх за допомогою нелінійних процесів в n-мірних просторах. Найбільш вивчені двовимірні процеси.
Якщо нелінійна динамічна система володіє декількома стійкими станами, то кожний стійкий стан володіє деякою областю початкових станів, з яких система обов'язково попаде в аналізовані кінцеві стани. Таким чином, фазовий простір системи розбивається на області тяжіння атракторів. Забарвлюючи області тяжіння різними кольорами, можна отримати колірний фазовий портрет цієї системи (ітераційного процесу). Міняючи алгоритм вибору кольору, можна отримати складні фрактальні картини з химерними кольоровими візерунками. Прикладом є множина Мандельброта.
3) Стохастичні фрактали.
Ще одним відомим класом фракталів є стохастичні фрактали, які виходять у тому випадку, якщо в ітераційнім процесі випадковим чином міняти якісь його параметри. При цьому виходять об'єкти дуже схожі на природні - несиметричні дерева, порізані берегові лінії і т. д. Двовимірні стохастичні фрактали використовуються при моделюванні рельєфу місцевості і поверхні моря.
