54.Рішення моделі в. Леонтьєва у випадку відсутності екзогенного споживання та його обліком.

Нехай екзогенний задана траєкторія споживання . В цьому випадку рішення системи має вигляд:

де коефіцієнти 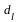визначаються виходячи з початкової умови:

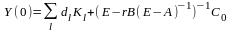
Матриця 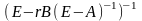є структурним аналогом коефіцієнта скалярної моделі .

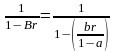З’ясуємо, чи можливе в моделі при заданій траєкторії споживання зростання без обмеження, іншими словами, чи існують обмеження на темп r.

Нехай в першому доданку домінує темп, відповідний корінню Фробеніуса — Перону: . Нехай r > 1/s. Тоді з часом другий доданок в (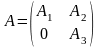 ) починає домінувати, оскільки перше тяжіє до темпу 1/s. Отже, 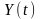все більшою мірою починає визначатися вектором . Позначимо . Узагальнюючи умову продуктивності, забезпечувану теоремою Фробеніуса - Перону, для матриці 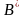одержуємо У даному випадку непродуктивна. Оскільки 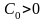, то одержуємо, що вектор містить негативні компоненти. Це значить, що рано чи пізно в з'являться негативні компоненти і траєкторія вийде в неприпустиму із змістовної точки зору область.

Таким чином, за наявності екзогенний заданій траєкторії споживання вигляду у структурній моделі існування допустимої траєкторії визначається співвідношенням r>1/s. Якщо домінує експонента з темпом, не відповідним темпу Фробеніуса - Перрона, то за результатами аналізу при С (t) = 0 траєкторія все одно вийде в неприпустиму зі змістовної точки зору область.

55.B чому сутність стохастичних моделей економічної динаміки?

Модель оцінки валютних потоків в умовах кризи. Змоделюємо загальну схему руху грошово-фінансових і товарних ресурсів. Уведемо ряд позначень:

W_вx(t,i) — швидкість приходу деякого ресурсу в i -й вузол, (кількість/час);

W_виx(t,i) — швидкість відходу деякого ресурсу з i - го вузла;

W_утв (t,i) — швидкість утворення деякого ресурсу в i-м вузлі;

W_зн(t,i) — швидкість зникнення деякого ресурсу в i -м вузлі;

W_зм(t,i) — швидкість зміни вартості капіталу в i -м вузлі за рахунок макропричин;

с_вx(t, i) — ціна одиниці кількості вхідного потоку в i –й вузол;

c_вих(t, i) — ціна одиниці кількості вихідного потоку з i -го вузла;

V(t, i) — величина деякого ресурсу, накопичена в i -м вузлі.

B найпростішому випадку зміна ресурсу V буде описуватися рівнянням:

Зміна вартості у грошові формі буде задовольнять рівнянню:

D [c(t,i)·V(t,i)]/dt = c_вx(t, i)·W_вx(t, i)- c_вих(t, i) ·W_виx(t, i)+W_зм(t, i).

Модель валютної паніки. Паніка за своєю природою є ланцюговим, лавиноподібним процесом, що розвивається в середовищі з великою, разом з тим, обмеженою кількістю учасників. До такого роду процесів у природі відповідають епідемії, хімічні реакції, у соціально-економічній сфері - валютні, біржові паніки, створення й розвиток фінансових «пірамід», поширення реклами й та ін.

Будемо вважати, що кількість (N) тримачів грошей велика, сума вільних коштів у кожного тримача однакова. Кількість бажаючих поміняти ці кошти на валюту в початковий момент часу t₀ дорівнює п₀. Цих бажаючих можна назвати «зараженими» вірусом паніки і їх кількість на момент часу t — n (t).

Тоді рівняння для частини «заражених» k(t):

dk(t)/dt=(1- k(t))·(1-e ^-r·k(t)),

де k(t)=n(t)/N.

Модель Самуельсона-Хікса з періодичними коефіцієнтами. Представимо ще один приклад стохастичної моделі економічної динаміки.

Розглянемо рівняння моделі Самуельсона - Хікса:

C(t)= ·Y(t-1)+C;

I(t)= ·Y(t-1)- Y(t-2)+I;

Y(t)= C(t)+ I(t)+ G(t),

де Y(t) — національний доход у момент часу t; C(t) - споживання; I(t) -інвестування; G(t) — державні витрати; 0 < < 1 — гранична схильність до споживання; а — акселератор; C — автономне споживання; I — автономне інвестування.