
- •1.Вплив часу на параметри моделі Самуельсона - Хікса.
- •2.Моделі дискретної економічної динаміки.
- •3.Які системи вивчаються в теорії катастроф?
- •4.Модель рівноваги Вальраса.
- •5.B чому сутність моделі валютної паніки?
- •6.Які висновки можна зробити за моделями?
- •7.З чого складається властивість стійкості системи?
- •8.Дискретна й безперервна моделі попиту та пропозиції.
- •9.Моделі динаміки суспільного продукту і національного доходу.
- •12.Які існують види фракталів?
- •11.Поняття про стабільність лінійних систем.
- •13.Розв’язування диференційних рівнянь макроекономічної динаміки.
- •14.Які типи катастроф існують у двовимірному випадку?
- •15.Стабільність і рівновага в динамічних системах.
- •16.Розходження в поводженні моделі в. Леонтьєва при зміні структурних коефіцієнтів моделі.
- •17.Опишіть зміни капіталовкладень й інших показників у різних варіантах моделі Гудвіна.
- •18.Основні положення моделі Харрода - Домара.
- •19.Що є джерелом хаотичного поводження системи?
- •22.Що затверджує теорема Ляпунова про стійкість?
- •23.Які методи застосовуються для виявлення хаотичного поводження?
- •20.B чому відмінність поняття стійкості для стохастичних систем?
- •25.Який зв'язок фракталів і хаосу?
- •21.Проведіть аналіз дисипативних систем для макроекономіки.
- •24.B чому розходження й спільність підходів ідей різних шкіл?
- •26.B чому суть модифікацій моделей економічних циклів Гудвіна?
- •27.Які випадкові процеси називаються стійкими?
- •28.Що являють собою вузол, сідло, фокус, центр?
- •29.Які основні якісні характеристики складної системи? Дайте коротке пояснення кожній властивості.
- •31.B чому полягає розходження поводження й розвитку системи?
- •30.Яким чином ураховуються виробничі цикли в моделях динаміки корисності споживчих благ?
- •32.У чому полягає основне завдання якісного аналізу динамічних систем?
- •33.Сформулюйте основні положення синергетики.
- •34.B чому відмінність хаотичного поводження від випадкового?
- •35.Яка система називається динамічною? Якими складовими формально описується динамічна система?
- •36.Які виділяються типи стійкості стану системи?
- •37.Методи розв'язання дискретної й безперервної моделі попиту та пропозиції.
- •38.Поняття про допустимість стану й траєкторії моделі в. Леонтьєва.
- •42.Взаємозв’язок акселератора з мультиплікатором.
- •39.Типи поведінки економічної системи.
- •40.Ha яких рівняннях заснована дана модель?
- •43.Що мається на увазі під біфуркацією?
- •41.Які виділяються види диференціальних рівнянь 1-го порядку?
- •44.B чому суть моделі, запропонованої в. С. Михалевичем?
- •45.Які методи можна застосувати для управління хаотичними системами? b чому їхні переваги й недоліки?
- •46.Критерії та умови оптимізації.
- •47.Розв’язування задач оптимального управління.
- •53.B чому сутність технологічної концепції суспільної еволюції?
- •48.Стійкість загальної рівноваги Вальраса.
- •49.Ha яких економічних законах засновані ефекти, отримані в моделі динаміки корисності споживчих благ?
- •50.Нормальна ціна в павукоподібній моделі.
- •51.Як у даній моделі відбивається платоспроможний споживчий попит?
- •52.Характеристики швидкості та інтенсивності зміни динамічного ряду.
- •54.Рішення моделі в. Леонтьєва у випадку відсутності екзогенного споживання та його обліком.
- •55.B чому сутність стохастичних моделей економічної динаміки?
- •56.Яким образом може бути представлена потенційна функція системи при наявності катастрофи?
- •57.Для чого застосовуються фрактали в дослідженні складних систем?
- •58..Які види перетворень використовуються для опису динамічних характеристик систем?
- •59.Які причини появи синергетики і її часткових напрямів?
- •60.B чому розходження системного й синергетичного підходів до дослідження складних систем?
- •63.Які припущення використовуються в моделях економічних циклів Гудвіна?
- •61.Найпростіша динамічна модель з мультиплікатором.
- •62.Основні припущення моделі в. Леонтьєва.
- •64.У чому відмінності кількісних, структурних і якісних змін у системах?
- •67.Показники економічної динаміки.
- •65.Які явища в поводженні системи можуть указувати на наявність катастрофи?
- •66.Якою формальною моделлю можна видобразити грошові й товарні потоки?
- •68.Охарактеризуйте модель оцінки валютних потоків.
- •69.Що таке атрактори і які їх основні види?
- •70.Чим пояснюється наявність біфуркації в поводженні системи?
- •71.Модель зовнішньої торгівлі.
- •72.Що означає стійкість системи?
- •73.У чому відмінність загального й приватного розв’язання диференціального рівняння
- •74.Визначення найкращого темпу приросту споживання.
- •75.Закон збереження ресурсу й грошова форма збереження ресурсу.
- •76.Охарактеризуйте основні поняття самоорганізації?
- •78.Проінтерпретуйте поняття граничний цикл і фазові переходи.
- •79.Наведіть приклади, що описують розвиток валютної паніки?
- •80.Як ураховується нестаціонарний випадок для даної моделі?
- •81.Який вид має звичайне диференціальне рівняння? Система диференціальних рівнянь?
- •82.Проведіть аналіз розв'язань в моделях економічних циклів.
- •83.Які існують різні механізми якісних змін?
- •84.Що являє собою траєкторія поводження системи?
- •85.Що являє собою рівноважний стан системи?
- •86.Багатофакорні моделі економічного зростання
- •87.Якими факторами визначається динаміка корисності споживчих благ у зазначених моделях?
- •88.Критерій стійкості Гурвіца.
- •89.Основні показники економічної динаміки при неперервних змінах.
- •90.Якими методами в даній моделі вирішується система диференціальних рівнянь?
- •91.Проведіть аналіз моделі Самуельсона - Хікса.
- •92.Які явища називаються фракталами?
- •93.Поняття технологічного темпу приросту випуску продукції.
- •94.Наведіть приклади швидких процесів в економіці.
- •77.B чому розходження понять «рівновага», «стійкість» і «стаціонарність»?
- •95.Яким чином здіснюється якісний аналіз?
- •96.B чому проявляється катастрофа типу складка, зборка?
- •97.Як проводиться класифікація станів рівноваги для систем другого порядку?
- •98.Що являє собою функція катастрофи?
- •99.Які основні вимоги пред'являють до макромоделей і параметрів їхнього опису?
- •100.Що означає розв'язати диференціальне рівняння?
- •101.Предмет і завдання моделювання макроекономічної динаміки.
- •102.Моделі неперервних динамічних систем в економіці.
- •103,Що вивчає економічна динаміка?
- •104,Загальний вид рівнянь динамічної моделі в. Леонтьєва.
- •105,Макроекономічні динамічні виробничі функції.
- •Вплив часу на параметри моделі Самуельсона - Хікса.
- •Моделі дискретної економічної динаміки.
26.B чому суть модифікацій моделей економічних циклів Гудвіна?
У
закритій економіці без економічної
активності держави завдяки гнучкій
системі цін на ринку благ постійно
існує рівновага; відповідно об'єм
інвестицій дорівнює об'єму заощаджень.
Внаслідок
зростання населення і технічного
прогресу національний дохід країни
щорічно збільшується. Річний темп
зростання населення рівний (1 + n), а
технічний прогрес виражається в
щорічному збільшенні середньої
продуктивності праці в (1 +
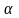 )
раз.
)
раз.
У цій моделі кон'юнктурні цикли виникають внаслідок зміни розподілу національного доходу між працею і капіталом.
wN/y
- доля праці в національному доході;
y/N=q - середня продуктивність праці;
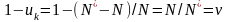 -
показник зайнятості; K/y=
-
показник зайнятості; K/y=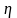 - капіталоємність національного
доходу;
- капіталоємність національного
доходу;
 -
темп приросту показника x в періоді t.
-
темп приросту показника x в періоді t.
Долю
праці в національному доході, що є
головним об'єктом уваги в цій моделі,
можна представити у вигляді
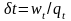 .
Оскільки при безперервному зростанні
темп приросту дробу дорівнює різниці
темпів приросту чисельника і знаменника,
а продуктивність праці по припущенню
росте з постійним темпом
,
то
.
Оскільки при безперервному зростанні
темп приросту дробу дорівнює різниці
темпів приросту чисельника і знаменника,
а продуктивність праці по припущенню
росте з постійним темпом
,
то
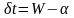 /
/
Темп
зміни ставки реальної заробітної плати
(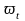 )
відповідно до кривої позитивно залежить
від рівня зайнятості і в цій моделі
визначається по формулі
)
відповідно до кривої позитивно залежить
від рівня зайнятості і в цій моделі
визначається по формулі
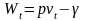 , де p
і
, де p
і
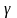 - позитивні константи.
- позитивні константи.
На
основі встановлених залежностей темп
приросту долі праці в національному
доході можна представити у виді:
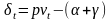
Приріст
капіталу визначається об'ємом інвестицій:
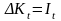 .
Тому темп капіталу дорівнює
.
Тому темп капіталу дорівнює
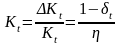 .
Ці два диференціальних
рівняння складають модель Гудвіна, що
описує кон’юнктурні колебання економіки.
В
цій моделі
кон'юнктурні
цикли виникають внаслідок зміни
розподілу національного доходу між
працею і капіталом.
Внаслідок перегріву економіки, що
відбулося в попередній фазі, виникає
спад виробництва. Незважаючи
на зниження зайнятості і ціни праці,
частка праці в національному доході
продовжує збільшуватися внаслідок
випереджального скорочення прибутку.
.
Ці два диференціальних
рівняння складають модель Гудвіна, що
описує кон’юнктурні колебання економіки.
В
цій моделі
кон'юнктурні
цикли виникають внаслідок зміни
розподілу національного доходу між
працею і капіталом.
Внаслідок перегріву економіки, що
відбулося в попередній фазі, виникає
спад виробництва. Незважаючи
на зниження зайнятості і ціни праці,
частка праці в національному доході
продовжує збільшуватися внаслідок
випереджального скорочення прибутку.
27.Які випадкові процеси називаються стійкими?
Випадко́вий проце́с — це випадкова величина, що змінюється з часом (іншими словами це набір випадкових величин, параметризованих величиною T — часом). Розрізняють випадкові процеси з дискретним і неперервним часом.
Випадковий процес трактується як стан певної системи, що змінюється випадково із часом. Якщо розглядати стан системи лише в дискретні моменти часу, то дістаємо випадкову послідовність або процес із дискретним часом.
Для випадкових подій які мають властивістю стійкості, відносну частоту наступу події природно вважати ступенем можливість настання випадкового події.
28.Що являють собою вузол, сідло, фокус, центр?
Атрактор — множина точок у фазовому просторі, до якої збігаються фазові траєкторії дисипативної системи.
Атрактори можуть бути точковими (точки рівноваги), лініями (граничні цикли), поверхнями, і навіть складними фрактальними стурктурами, як у випадку дивного атрактора. Навколо атрактора в фазовому просторі існує басейн притягання.
Якщо відкладати на фазовій площині різні типи рішень і давати назви відповідним особливим точкам, якщо рішення динамічної системи асимптотично прагнуть до особливої точки, то ця особлива точка називається стійким вузлом. Якщо траєкторії рішення розходяться так само від особливої точки, то її називають нестійким вузлом.
Якщо рішення x(t) і y(t) прагнуть до особливої точки, при цьому осцилюючи, то ця особлива точка називається стійким фокусом. У міру збільшення часу осциляції затухають і стають усе менш помітними, і, відповідно, траєкторія динамічної системи все ближче і ближче наближається до фокусу, як би накручувавшись на нього.
У центрі цього сімейства рішень знаходиться особлива точка (0,0). Природно, що це нерухома точка, оскільки вона є рішенням відповідної системи рівнянь алгебри. Якщо маятник без загасання знаходитиметься спочатку в цій точці, то він в ній залишиться в плині нескінченного часу. Таку особливу точку називають стійким центром.
У разі двох функцій x(t), y(t), тобто фазового портрета на площині, може спостерігатися трохи складніше поєднання. Одна і та ж особлива точка може бути стійка, наприклад, по х(t), і нестійка по y(t). Таку особливу точку називають сідлом.
