2. Повна похідна

Означення. Нехай – нормовані простори. Відображення називається диференційованим у точці , якщо існує таке лінійне неперервне відображення що , де при , тобто .

Означення. Лінійна відносно h функція називається дотичним відображенням або похідною відображення в точці х. Позначення: .

Теорема. Якщо відображення диференційоване у точці , то його похідна єдина. У цьому випадку f неперервне в х. Крім того, у точці х відображення f має похідну вздовж будь-якого напрямку , а відображення лінійне неперервне відображення і .

Доведення. Нехай , покладаючи в означенні похідної маємо , або

, при отримаємо, що ,

тобто f має похідну в точці х у будь-якому напрямку, і неперервне і лінійне по l.

Покажемо, що похідна єдина. Якщо і – похідні f, то , , тобто .

Неперервність f у точці х випливає з рівності , тобто маємо .

Нехай диференційована в кожній точці , тобто диференційована на Х, то виникає функція , яку називають похідною від f або похідним відображенням. Значення в точці – лінійне неперервне відображення , яка є диференціалом або похідною функції f у даній конкретній точці .

Зауважимо, що в силу означення диференційованості випливає, що відображення, диференційоване в точці – неперервне у цій точці. Обернене невірне, наприклад, функція в точці х=0 неперервна, але не диференційована.

Зауваження. Умову диференційованості у точці можна записати так: , при . Зрозуміло, що означення насправді відноситься до відображень будь-яких афінних просторів , лінійні простори Х і Y яких нормовані.

Приклади.

1. , Х – скінчено вимірна зі скалярним добутком, - ортонормований базис в Х, а де то

2. Якщо , то для будь-якого напрямку

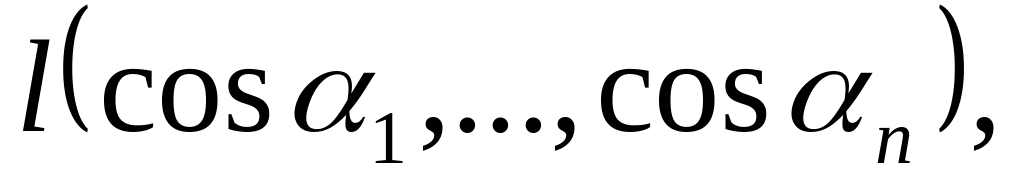
Отже

3. Нехай , де – скінчено вимірні зі скалярним добутком. Якщо , 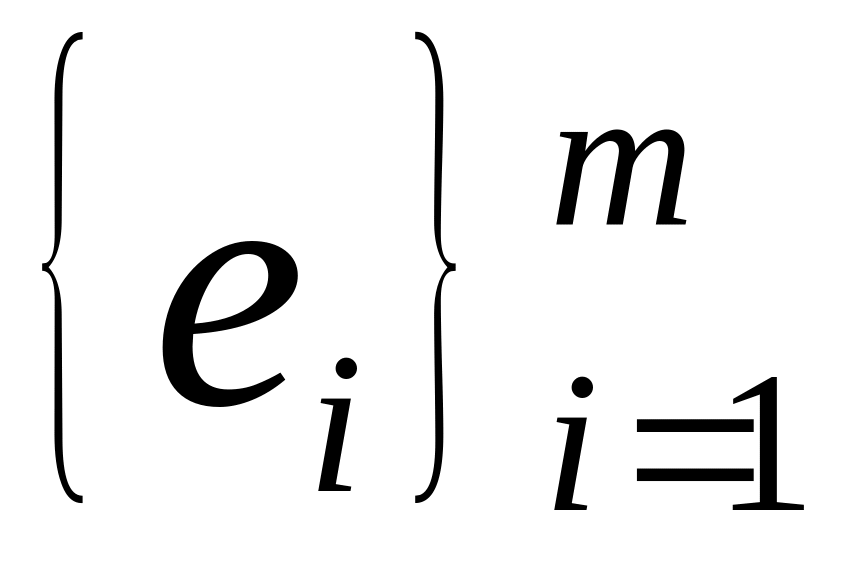- ортонормовані базиси у і відповідно.

, маємо, для будь-якого

.

У координатній формі запису

Отже (у координатній формі запису).

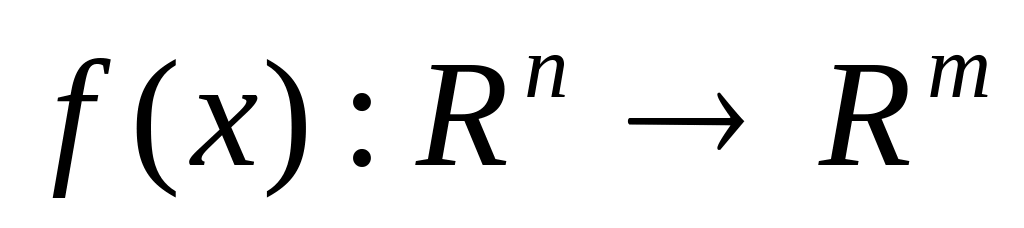4. Якщо , то Отже, з приклада 3 маємо

.

Якщо і існує у деякій точці х, то існують (х), тобто існує матриця Якобі у х.

Але обернене твердження невірне. Наприклад:

Але в (0,0) функція не неперервна, значить і не диференційована.

Практичне заняття №9 Тема: Частинні похідні. Похідна у напрямку. Повна похідна.

Основні відомості:

1. Означення похідної у напрямку.

2. Означення та властивості повної похідної.

Задачі

1.1. Знайти .

1.2. . Знайти та матрицю Якобі.

1.3. . Знайти .

2.1.

Знайти .

2.2.

Обчислити , де , а l – направлення від до .

2.3. . Обчислити , де у направленні l, що утворює з осями координат кути 60º, 45º, 60º відповідно.

3.1. . Знайти .

3.2. . Знайти .

3.3. Знайти .

Задачі для самостійного розв’язку.

1. Знайти .

2. Знайти .

3. Знайти .

4. . Знайти .

5. .

Знайти .

6. . Знайти .

7. . Знайти .

8. , . Знайти .

9.

Знайти , де у направленні бісектриси першого координатного кута.

10. Знайти похідну функції у точці в напрямку променя, який утворює кут з віссю абсцис.

11. Знайти похідну функції в точці у напрямку, що йде від цієї точки до точки .

12. Нехай . Знайти та , .

13. Знайти , , .

14. . Знайти .

15. Знайти та , .