4. Правило Лопіталя.

Теорема. Нехай функції і диференційовані на , причому на і при . Тоді в кожному з двох випадків

1. при ,

2. при

буде існувати .

Доведення.

Доведемо випадок 1.

,

Функції визначені на неперервні та диференційовані на і задовольняють теорему Коші. Отже таке, що

або ,

Для будь-якої послідовності існує послідовність і

та .

Отже, за Гейне

Інший випадок розгляньте самостійно.

Практичне заняття №5 Тема: Правило Лопіталя. Використання похідної для розв’язання рівнянь, нерівностей, доведення нерівностей.

Основні відомості:

1. Правило Лопіталя.

2. Необхідна та достатня умова монотонності диференційованої функції.

3. Екстремальні точки функції.

4. Необхідна умова екстремальності точки.

5. Достатня умова екстремальності точки для диференційованої функції.

Задачі:

Обчислити границі:

1. 

2. 

3. 

4. 

Довести нерівності:

1. 

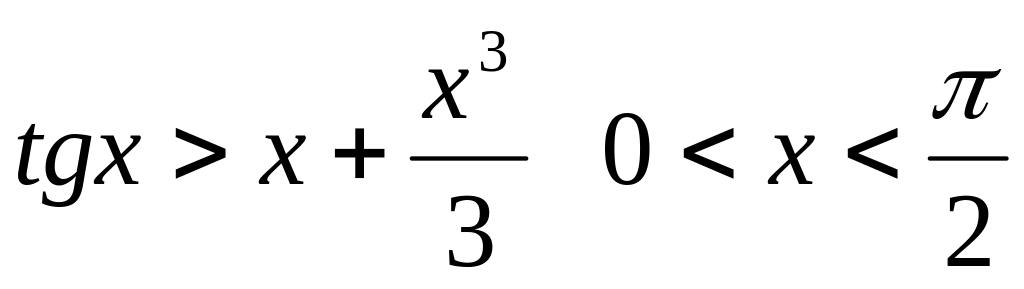
2. Що більше чи ?

Розв’язати нерівності:

3.1.

2. Знайти всі , при кожному з яких виконується нерівність , .

Завдання для самостійної роботи.

Обчислити границю:

1. 

2. 

3. 

4. 

5. 

6. 

8. 

9. 

10. 

11. 

12. 

13. 

14. 

15. 

Довести нерівності:

16. 

17. 

18. 

19. 

Вказівка: Використати заміну змінної.

20. 

Вказівка: Використати заміну змінної.

Розв’язати нерівності:

21. 

22. 

23. 

Знайти всі значення параметру а, при яких виконується нерівність:

24. 

25. 

Практичне заняття №6 Тема: Використання похідної для розв’язання рівнянь, доведення тотожностей, розв’язання задач на мінімаксимум.

Основні відомості:

1. Екстремальні точки.

2. Необхідна та достатня умови екстремальності точки.

Задачі:

Розв’язати рівняння:

1. 

2. При яких значеннях рівняння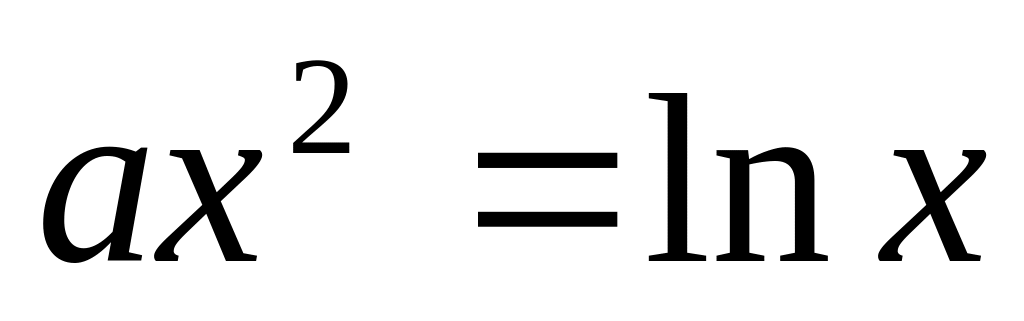 має один корінь?

Довести тотожності:

1. 

2. 

3.1. Яким повинен бути кут примикання дороги СЕ до автомагістралі АЕВ, щоб трата часу на перевіз за маршрутом АЕС була найменшою, якщо швидкість руху автомобілів по магістралі планується рівною , а по під’їзній дорозі ?

3.2. На лісопильних рамах деревину часто розпилюють на квадратний брус і чотири дошки з якнайбільшою площею поперечного перерізу. Яким повинно бути розміщення пил для такої розпилки?

Завдання для самостійної роботи.

Розв’язати рівняння:

1. 

2. 

3. 

4. 

5. 

Скільки розв’язків має рівняння:

6. 

7. 

При яких значеннях параметру має розв’язок рівняння:

8. 

9. 

10. 

Довести тотожності:

11. 

12. 

13. 

14. 

15. 

16. З усіх прямокутників даної площини визначити той, периметр якого найменший.

17. При яких лінійних розмірах зачинена циліндрична банка даної місткості 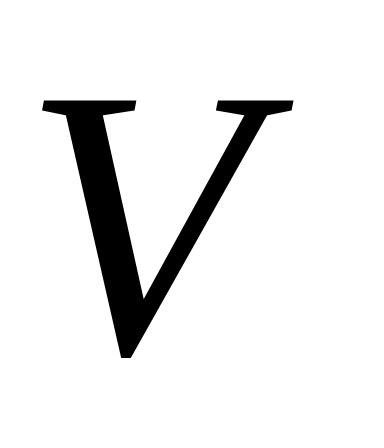буде мати найменшу повну поверхню.

18. Добові трати при плаванні судна складаються з двох частин, постійної, яка дорівнює а грн., та змінної, зростаючої пропорційно кубу швидкості. При якій швидкості плавання судна буде найбільш економним?

19. Камінь кинуто з заданою початковою швидкістю під кутом до небосхилу. Не враховуючи опір повітря, визначити при якому довжина польоту каменю буде найбільшою.

20. До річки шириною м. побудовано канал під прямим кутом шириною м. Якої максимальної довжини деревину можна провести з річки до каналу?

21. Пункт С розміщено в 50 км. від А і в 30 км. від магістралі, яка проходить через А. Під яким кутом до магістралі необхідно провести під’їзний шлях із С, щоб вартість перевезення з А до С та з С до А була найменшою, якщо відомо, що вартість перевезення по магістралі в 2 рази дешевша, ніж по під’їзному шляху?

22. В точках А та В знаходяться джерела світла силою відповідно та кандел. На відрізку АВ = а. знайти найменш освітлену точку М.

23. На якій висоті над центром круглого столу радіуса а необхідно розмістити електричну лампу, щоб освітлення краю столу була найбільшою?

Вказівка: Яскравість освітлення виражається за формулою , де - кут нахилу променів, - відстань до джерела, - сила джерела світла.

24. В трикутник з основою та висотою вписати прямокутник з найбільшою площею.

25. Знайти прямокутний трикутник найбільшої площини, якщо сума його катета та гіпотенузи постійна.