
- •Передмова
- •Лекція №1 Похідна функції однієї змінної. Властивості.
- •Похідна, диференціювання та їх зв’язок.
- •Основні властивості диференційованих функцій.
- •3. Основні теореми диференціального числення для функції однієї змінної.
- •1. Теореми Роля і Лагранжа.
- •Похідна вищого ґатунку. Формула Тейлора.
- •Практичне заняття №1 Тема: Похідна. Диференційованість функції.
- •Практичне заняття №2 Тема: Властивості функцій диференційованих на відрізку.
- •Практичне заняття №3 Тема: Похідні та диференціали вищих порядків. Формула Тейлора.
- •Практичне заняття №4 Тема: Формула Тейлора. Обчислення границь за допомогою формули Тейлора.
- •1. Дослідження монотонності.
- •2. Необхідна і достатня умова локального екстремуму.
- •3. Опуклі функції.
- •4. Правило Лопіталя.
- •Практичне заняття №7 Тема: Дослідження функцій.
- •Скалярний добуток
- •2. Лінійні оператори.
- •3. Простори неперервних лінійних операторів. Норма оператора
- •Практичне заняття №8 Тема: Лінійний нормований простір зі скалярним добутком. Лінійні оператори.
- •Лекція №4 Похідна у напрямку. Частинні похідні. Повна похідна.
- •1. Похідна у напрямку.
- •2. Повна похідна
- •Практичне заняття №9 Тема: Частинні похідні. Похідна у напрямку. Повна похідна.
- •Лекція №5 Геометрична інтерпретація похідної відображення. Градієнт.
- •1. Геометрична інтерпретація похідної відображення.
- •2. Градієнт дійсної функції в евклідовому просторі. Механічний зміст градієнта.
- •Практичне заняття №10 Тема: Геометричний зміст похідної функції. Механічний зміст похідної.
- •Лекція №6 Диференціал. Загальні закони диференціювання
- •1. Диференціал
- •2. Загальні закони диференціювання.
- •Практичне заняття №11 Тема: Диференціал функції. Загальні закони диференціювання.
- •Лекція №7 Формула скінчених приростів
- •Теорема про скінчений приріст. Нижче всюди будемо припускати, що і - лінійні, нормовані, повні простори.
- •Достатні умови диференційованості функції. Спочатку узагальнимо означення частинної похідної та випадок декартового добутку нормованих просторів.
- •Лекція №8 Похідні вищих порядків. Формула Тейлора.
- •1. Похідні вищих порядків. Означення. Приклади в
- •2. Симетричність похідної вищого порядку
- •3. Формула Тейлора. Приклади в і
- •Практичне заняття №12 Тема: Похідна та диференціал вищого порядку. Формула Тейлора.
- •1. Дослідження внутрішніх екстремумів
- •2. Необхідні і достатні умови екстремуму у випадку
- •Практичне заняття №13 Тема: Дослідження екстремумів у випадку функцій кількох змінних.
- •Лекція №10 Теорема про неявну функцію
- •1. Теорема про неявну функцію
- •2. Обернена функція.
- •Лекція №11 Умовні екстремуми
- •Необхідна умова умовного локального екстремуму.
- •Випадок відображення
- •Достатня умова умовного локального екстремуму.
- •Практичне заняття №14 Тема: Умовні локальні екстремуми.
- •Література
Практичне заняття №2 Тема: Властивості функцій диференційованих на відрізку.
Основні відомості: Теореми Роля, Лагранжа, Коші.
Задачі:
Довести, що якщо рівняння
 має додатній корінь
має додатній корінь ,
то рівняння
,
то рівняння
 також має додатній корінь і при тому
менший
також має додатній корінь і при тому
менший .
.Довести, що якщо
 диференційована
разів
на відрізку
диференційована
разів
на відрізку і обертається на ньому в нуль в
і обертається на ньому в нуль в
 точці, то існує таке
точці, то існує таке
 ,
що
,
що .
.
Довести, що
 ,
при умові
,
при умові
 .
.
Довести, що якщо
 диференційована та необмежена на
скінченому інтервалі
диференційована та необмежена на
скінченому інтервалі
 ,
то її похідна також необмежена на цьому
інтервалі.
,
то її похідна також необмежена на цьому
інтервалі.
Довести, що якщо диференційована на
 ,
то існує така точка
,
то існує така точка
 ,
що
,
що
 .
.
Нехай диференційована на
 ,
,
 .
Довести, що
.
Довести, що
 в деякій точці
в деякій точці
 .
.
Вказівка: розглянути функцію![]() .
.
Функція неперервна на та диференційована на
 .
Довести, що якщо
.
Довести, що якщо
 ,
то
,
то в
деякій
в
деякій .
.
Вказівка: розглянути
![]() .
.
Завдання для самостійної роботи.
Довести, що між двома дійсними коренями многочлена з дійсними коефіцієнтами є корінь його похідної.
Довести, що якщо всі корені многочленна
 з дійсними коефіцієнтами
з дійсними коефіцієнтами
 дійсні, то його послідовні похідні
дійсні, то його послідовні похідні

 також мають лише дійсні корені.
також мають лише дійсні корені.Показати, що рівняння
 не може мати двох різних коренів в
інтервалі
не може мати двох різних коренів в
інтервалі
 .
.Функція двічі неперервна диференційована на
 та має на
не менш трьох різних нулів. Довести, що
існує
та має на
не менш трьох різних нулів. Довести, що
існує
 ,
що
,
що .
.
Вказівка: використовувати задачу 3.3.
Довести
 .
.Довести
 .
.
Довести
 .
.Довести, що
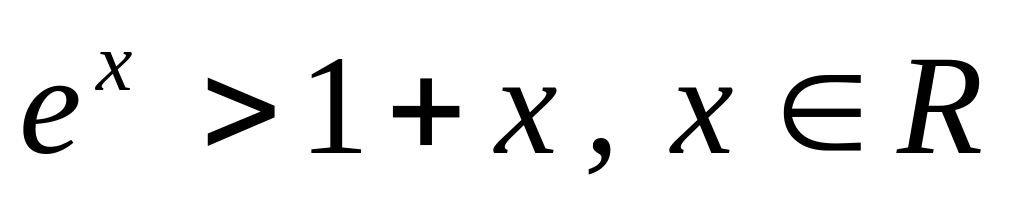 .
.Довести, що
 .
.Довести
 .
.Довести, що якщо диференційована разів при

 ,
а
,
а
 при
при
 ,
то і
,
то і
 при
при
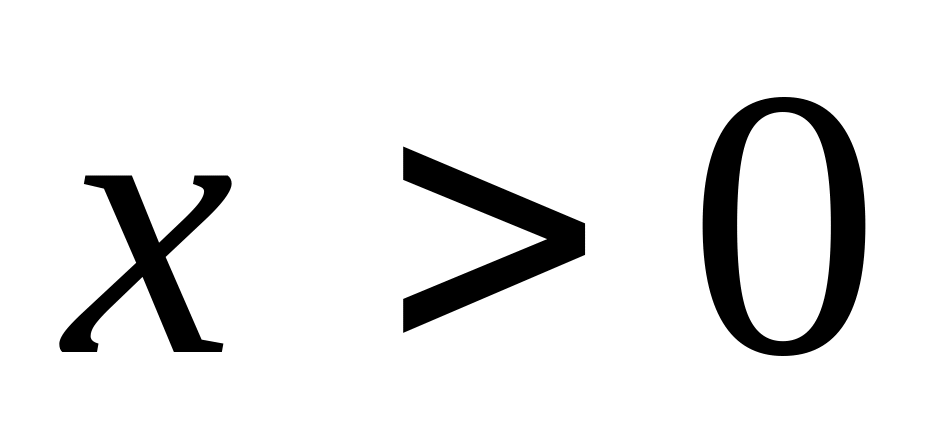 .
.Довести, що якщо та диференційовані разів при
 та
та
 ,
,
 при
,
то і
при
,
то і
 при
.
при
.
Довести, що якщо
 має в скінченому або нескінченому
інтервалі
має в скінченому або нескінченому
інтервалі
 обмежену
похідну
обмежену
похідну ,
то
рівномірно
неперервна на
.
,
то
рівномірно
неперервна на
.
Довести, що якщо диференційована при
 та
та
 ,
то
,
то
 .
.
Довести, що якщо диференційована на
 ,
то
,
то

 ,
де
,
де
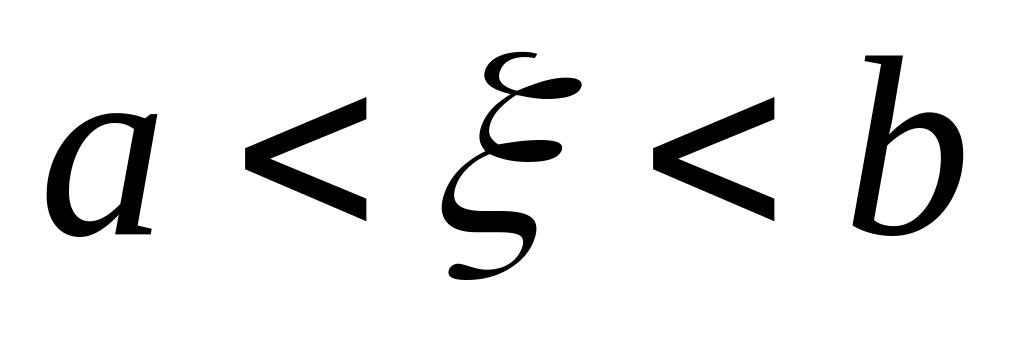 .
.
Вказівка: використовувати теорему Коші.
Довести, що якщо функція диференційована на
 ,
то існує така точка
,
то існує така точка
 ,
що
,
що .
.
Вказівка: розглянути функцію![]() .
.
Нехай неперервна диференційована на
 ,
та її похідна монотонна. Довести, що
якщо
,
та її похідна монотонна. Довести, що
якщо
 ,
то
,
то .
.
Довести, що якщо задовольняє умовам теореми Роля на
 і не є константа, то на цьому відрізку
існують такі точки
і не є константа, то на цьому відрізку
існують такі точки
 та
та
 ,
що
,
що
 .
.Довести, що якщо неперервна на і диференційована на та не є лінійна, то існує така точка , що
 .
.Довести, що якщо
 при
при
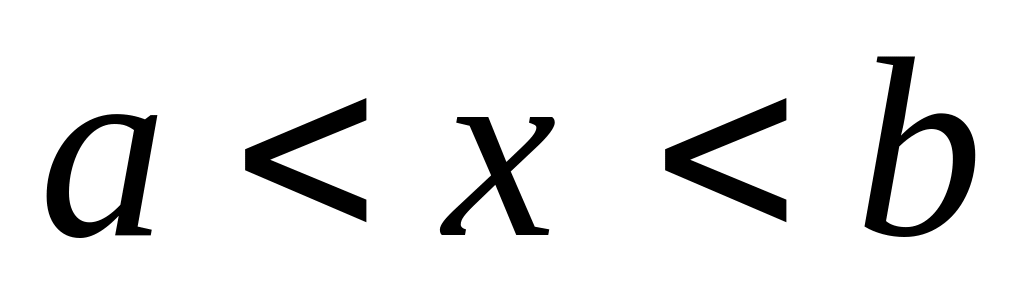 ,
то
,
то .
.Довести, що єдина
 ,
яка має постійну похідну
,
яка має постійну похідну є функція
є функція
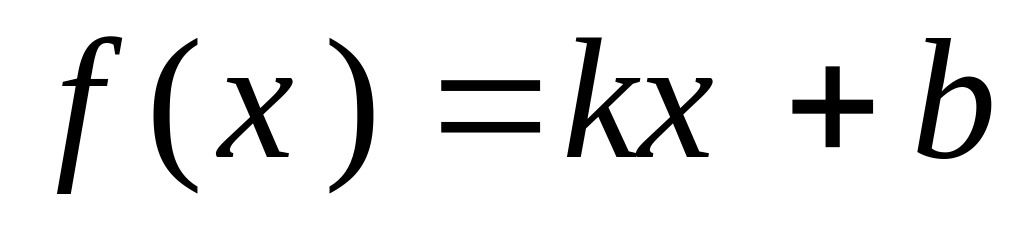 .
.Що можна сказати про , якщо
 ?
?Довести, що єдина функція
 задовольняє рівнянням
задовольняє рівнянням
 є
є
 -
довільна константа.
-
довільна константа.
Вказівка: розглянути
![]() .
.
Довести, що якщо , то
 ,
де
,
де .
.В умовах задачі 24 довести, що
 .
.
Практичне заняття №3 Тема: Похідні та диференціали вищих порядків. Формула Тейлора.
Основні відомості:
Визначення похідної та диференціала n-го порядку.
Формула Тейлора.
Розклад в ряд Маклорена основних елементарних функцій.
Задачі:
За допомогою формули Лейбниця та основних формул:
1.
![]() 2.
2.
![]()
3.
![]()
Розв’язати задачі:


Знайти
 ,
якщо
,
якщо
 ,
а
-
незалежна змінна.
,
а
-
незалежна змінна.Знайти , якщо
 ,
а
-
функція деякої незалежної змінної.
,
а
-
функція деякої незалежної змінної.
За допомогою формули Тейлора розв’язати задачі:
2.1. Нехай
![]() .
.
Довести, що
![]() .
.
Вказівка. Довести за допомогою індукції.
2.2. Нехай
![]() -
двічі диференційована функція та
-
двічі диференційована функція та
![]()
![]() Довести, що
Довести, що
![]() .
.
Вказівка: Розглянути
![]()
![]()
Розкласти в ряд Маклорена до
 .
.
Завдання для самостійної роботи.
Нехай
-
тричі диференційована функція. Знайти![]() та
та
![]() якщо:
якщо:
 .
. .
. .
. .
.
 -
тричі диференційована функція.
-
тричі диференційована функція.

Розклавши функцію на найпростіші дроби
знайти
![]()



 ,
де
,
де
 -
многочлен.
-
многочлен.
Нехай диференційована та задовольняє умові
 ,
де
має похідні всіх порядків. Довести,
що
має
похідні всіх порядків.
,
де
має похідні всіх порядків. Довести,
що
має
похідні всіх порядків.
Вважаючи незалежною змінною знайти :
Нехай
![]() -
функція від
:
-
функція від
:
 знайти
знайти
 .
. знайти
знайти
 .
.Нехай
 та
та
 ,
при чому
,
при чому
 при
при
 .
Довести, що
.
Довести, що при
при
 .
.
Вказівка.
![]()
![]()
Нехай
 - многочлен ступеня не вище
.
Довести, що
- многочлен ступеня не вище
.
Довести, що
![]() .
.
Розкласти за формулою Маклорена до
![]() :
:
