2. Випадок відображення

Нехай а ; відображення і

неперервно диференційовані.

Точка , яка задовольняє рівняння являється точкою умовного локального максимуму (мінімуму). Якщо існує окіл цієї точки такий що для будь якої точки , яка задовольняє рівнянню виконується нерівність .

Із загальної теореми будемо мати необхідну умову умовного локального екстремуму у слідуючому вигляді.

Теорема. Нехай неперервно-диференційовані в околі точки . Якщо (тобто )- має обернений), то необхідною умовою того, що точка - умовний локальний екстремум , при умові є існування дійсних постійних таких, що або

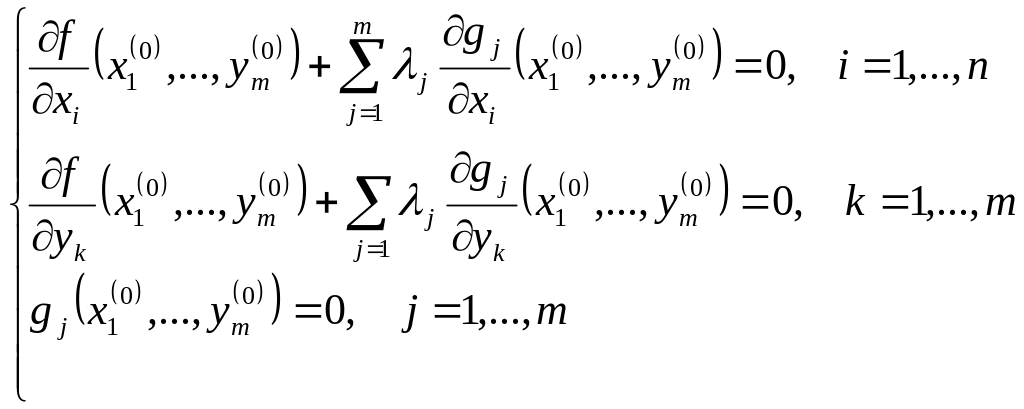
У термінах функції Лагранжа , ці умови мають вигляд:

Безпосереднє доведення цього факту легко знайти .

3. Достатня умова умовного локального екстремуму.

Повернемося до загальної ситуації. Припустимо, що точка задовольняє необхідним умовам умовного локального екстремуму у термінах функції Лагранжа. Якщо у функції Лагранжа замість підставити відображення , яка існує, згідно з теоремою про неявну функцію, то точка для функції буде локальним екстремумом тоді і тільки тоді, коли точка буде умовним локальним екстремумом для при умові . В зв’язку з цим, достатня умова умовного локального екстремуму у точці у термінах функції Лагранжа має вигляд:

1. Якщо , то в - умовний локальний мінімум.

2. Якщо , то в - умовний локальний максимум.

3. Якщо - змінює знак в залежності від , то у точці немає екстремуму.

Доведення цих умов випливає з того, що достатньою умовою екстремуму у для відображення є умова знакопостійності, незалежно від , форми та рівності

.

Підставляючи у рівність маємо

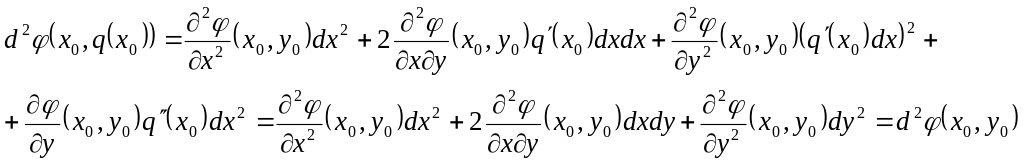
(ми врахували умову ).

Отже маємо, достатньою умовою умовного екстремуму в ( ) є знакопостійність форми незалежно від . Що стосується , що фігурує у формі , то його можна виразити через з рівності .

Приклад.

У випадку і достатня умова умовного екстремуму у точці має вигляд:

1. , то в - умовний локальний мінімум.

2. , то в - умовний локальний максимум

3. - змінює знак в залежності від , (зауважимо, що , фігуруючий у формі можна виразити через з рівностей ), то у точці не має екстремуму.

Практичне заняття №14 Тема: Умовні локальні екстремуми.

Основні відомості: 1. Означення умовного локального екстремуму.

2. Необхідна умова умовного локального екстремуму.

3. Достатня умова умовного локального екстремуму.

Задачі:

Дослідити на умовний екстремум

1.1. ,

1.2.

1.3.

2.1. На параболі знайти точку найменш віддалену від прямої

2.2. Знайти правильну трикутну піраміду даного об’єму, що має найменшу суму ребер.

Завдання для самостійної роботи

Дослідження на умовний екстремум

1.

2.

3.

4.

5.

6.

7. .

8.

9. Довести .

Вказівка: дослідити на умовний мінімум функцію при умові .

10. На площині знайти точку, сума квадратів відстаней якої до площин і була би мінімальною.

11. Знайти прямокутний паралелепіпед даного об’єму , що має мінімальну площу поверхні.

12. На еліпсі знайти точки, що найменше та найбільше удалині від прямої

13. Знайти найбільшу відстань точок поверхні від площини

14. Знайти сторони прямокутного трикутника, що при даній площині має найменший периметр.

15. Зі всіх прямокутних паралелепіпедів, що мають дану діагональ, знайти той, об’єм якого найбільший.