2. Симетричність похідної вищого порядку

Теорема. Якщо для форма у точці х визначена, то вона симетрична відносно будь-якої пари своїх аргументів, тобто не залежить від порядку .

Доведення. Скористаємось методом математичної індукції. Перевіримо справедливість для . Нехай і фіксовані вектори з Х. Розглянемо функцію від .

, визначену для векторів і таких, що . Тоді .

Оскільки має в точці х другий диференціал, то існує окіл точки х, у якому f диференційована. Будемо вважати t настільки малим, що аргументи в правій частині в F належать цьому околу точки х.

Скориставшись цими зауваженнями і наслідком теореми про скінчений приріст, матимемо:

і ,

.

Тоді матимемо . Це означає, що . Оскільки

, _то .

Припустимо, що при , тоді при (ми скористалися припущенням симетричності похідної k-го ґатунку), що і треба було довести.

У випадку відображення , з урахуванням достатньої умови диференційованості функції (див. лекцію 7) , та вигляду розглянемо означення.

Означення. Відображення називається k-раз диференційованою у точці , якщо у деякім околі точки х вона має всі частинні похідні k-го ґатунку неперервні у самій точці х.

Нехай , тоді для k-раз диференційованої функції не залежать від порядку диференціювання, так як

– базис в .

Нижче нам знадобиться наступний приклад.

Приклад. , А – симетричне. ,

–

.

Отже .

3. Формула Тейлора. Приклади в і

Теорема. Якщо відображення околу точки х нормованого простору Х в нормований простір таке, що f має в похідні до порядку включно, а в самій точці х має похідну порядку , то

при .

Доведення. Покажемо справедливість формули по індукції. При вона вірна в силу означення . Нехай формула вірна при . Тоді покажемо справедливість для . Розглянемо

, визначену в околі зі значеннями в , яка диференційована (в силу розглянутого прикладу). Тоді

. Застосуємо до формулу з теореми при , для функції , тобто

при .

Тоді за формулою скінчених приростів

, що і дає шуканий результат.

Приклади.

1. .

2. ,

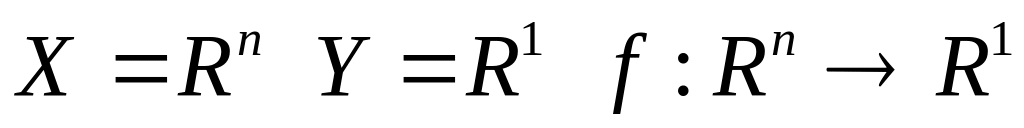Практичне заняття №12 Тема: Похідна та диференціал вищого порядку. Формула Тейлора.

Основні відомості:

1. Означення похідної та диференціала вищого порядку. Приклади в та .

2. Теорема про симетричність похідної k-го порядку.

3. Формула Тейлора.

Задачі:

1.1. , . Знайти , .

1.2. . Показати, що =

1.3. Знайти , , . Якщо .

1.4. , .

2.1. . Знайти .

2.2. . Знайти у точці .

2.3. . Знайти .

3.1. . Розкласти по степеням .

3.2. Знайти кілька перших членів розкладу функції по формулі Тейлора в точці (0,0).

3.3.Розкласти за формулою Тейлора в точці (0,0) функції а).

б)

Завдання для самостійної роботи

1. . Довести =

2. . Довести =

3. . Довести = = .

4. . Знайти .

5. . Знайти .

6. . Знайти .

7. . Знайти .

8. . Знайти у точці .

9. . Знайти .

10. . Знайти .

11. . Знайти .

12. . Обчислити , обмежившись членами до другого порядку включно.

13. Розкласти за степенями функцію , .

14. Розкласти по степенях і до другого порядку включно.

15. розкласти по степенях до третього порядку включно, та обчислити .

Розкласти по формулі Тейлора у точці (0,0)

16.

17.

18.

19.

20. , . Знайти .

21. , . Знайти .

23. , . Знайти .

Лекція №9 Дослідження внутрішніх екстремумів. Дослідження екстремумів у випадку функцій двох змінних