Лекція №7 Формула скінчених приростів

1. Теорема про скінчений приріст. Нижче всюди будемо припускати, що і - лінійні, нормовані, повні простори.

Теорема. Нехай неперервне відображення нормованого простору Х в нормований простір Y. Якщо на відрізку

функція f диференційована у всіх точках інтервалу , то

Доведення. Покажемо нерівність для будь-якого відрізку . Супремум береться на всьому відрізку . Позначимо , . Скористаємося співвідношенням справедливим для невід’ємних чисел, які задовольняють умовам: , .

При це очевидно. В силу однорідності воно справедливе в загальному випадку. Припустимо, що нерівність, яку треба довести не виконується, тобто . Тоді відрізок розіб’ємо пополам на два відрізка і відповідно позначимо і і прирости функції і . Для одного з одержаних відрізків буде виконуватись нерівність (*). Розбиваючи цей відрізок пополам і повторюючи далі всю процедуру отримаємо послідовність , .

Нехай , яка існує оскільки Х - повний простір. Виконавши додатково розбиття кожного з відрізків точкою і знову обираючи той, для якого виконується нерівність (*), одержимо послідовність відрізків, один кінець яких , а інший , але , так як і 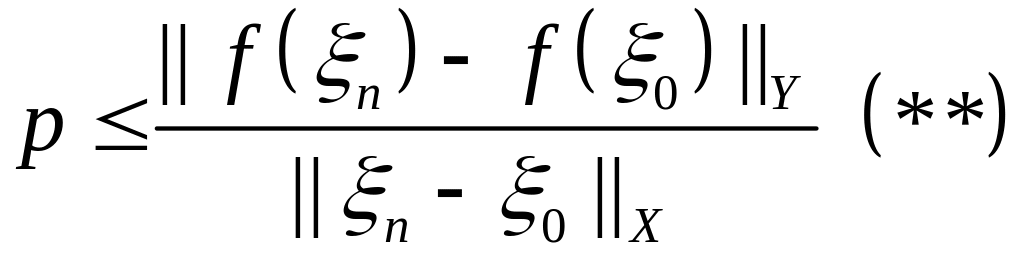, але f диференційована в , тобто при .

Значить, взявши так, що при достатньо великих будемо мати , що суперечить одержаній нерівності (**). Таким чином, припущення невірне і

Спрямувавши в силу неперервності f і нерівності одержимо твердження теореми.

Наслідок. Якщо , а , що задовольняє теоремі про скінчений приріст, то

.

Доведення. Розглянемо відображення , . Тоді задовольняє теоремі про скінчений приріст ,

, ,

.

2. Достатні умови диференційованості функції. Спочатку узагальнимо означення частинної похідної та випадок декартового добутку нормованих просторів.

Нехай , де - нормовані простори. При фіксованих розглянемо функцію

,

якщо вона в точці має похідну, то будемо називати її частинною похідною функції у точці у напрямку х і позначати .

Відмітимо, що означення, яке приводилось раніше, випливає з цього, якщо простір натягнутий на орт , тоді частинна похідна , де , тобто обидва означення співпадають.

Теорема. Нехай окіл точки х нормованого простору , що є прямим добутком нормованих просторів , і нехай , Y – нормований простір. Якщо в U відображення f має усі частинні похідні, то при умові їх неперервності у точці х відображення f диференційоване в цій точці.

Доведення. Доведемо для спрощення при . Перевіримо, що лінійне відносно відображення і є похідна f у точці х .

.

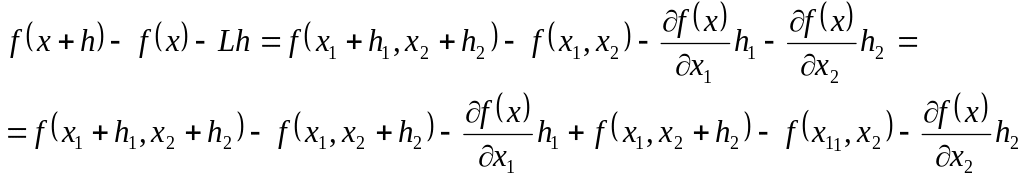З наслідку теореми про скінчений приріст маємо,

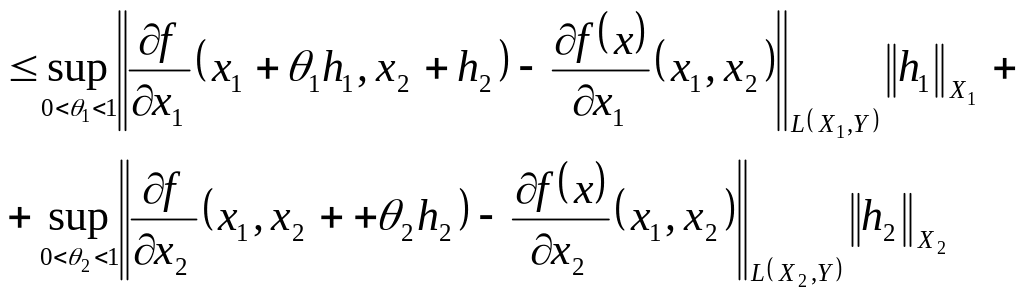
Оскільки , то з неперервності частинних похідних , в точці очевидно слідує, що права частина при , тобто .

Приклад. При маємо диференційованість в х якщо існують в деякому околі точки х і неперервні в х.

Зауваження. Доведено, що якщо і диференційоване, то , .

Лекція №8 Похідні вищих порядків. Формула Тейлора.

1. Похідні вищих порядків. Означення. Приклади в

Нехай – нормовані, повні простори і f – диференційоване і . Якщо означена в деякому околі х і диференційоване відображення, то його похідне відображення називається другим похідним відображенням і позначається .

Означення. Похідним відображенням порядку відображення у точці називається похідна в цій точці до похідного відображення порядку від f. , тобто можна інтерпретувати як - лінійний неперервний оператор.

Для конкретизації цього означення може бути вдало використано поняття похідної за направленням.

При в розумінні означення, раніше зазначеного;

при , то фіксуючи , а обчисливши значення оператора на матимемо

,

отже , тому .

Крім того, з означення похідної у напрямку, матимемо

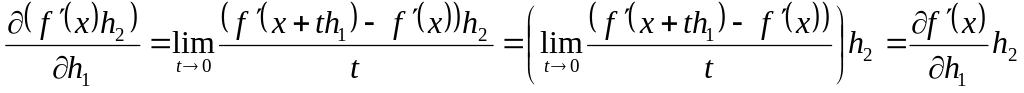, тобто .

Аналогічно,

Приклад.

, .

Для будь-яких ,

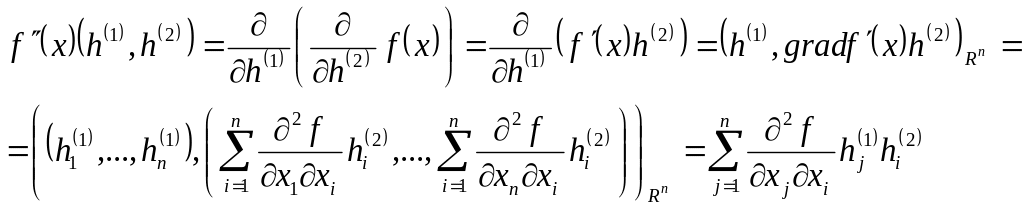
Отже

Аналогічно

Д ля будь-якого k будемо мати

Крім того, нижче будемо називати диференціалом k-го ґатунку в точці х відображення вираз , де довільний вектор . У випадку нашого прикладу, , маємо

,

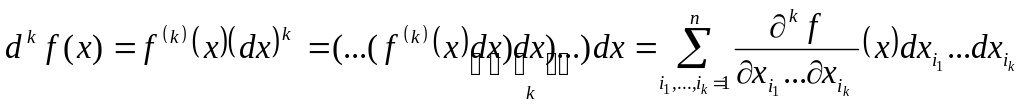де .