70

Лекційно-практичний курс

з математичного аналізу.

Частина 2. Диференціальне

числення.

Содержание

Передмова 3

Лекція №1 Похідна функції однієї змінної. Властивості. 4

Практичне заняття №1 Тема: Похідна. Диференційованість функції. 7

Практичне заняття №2 Тема: Властивості функцій диференційованих на відрізку. 9

Практичне заняття №3 Тема: Похідні та диференціали вищих порядків. Формула Тейлора. 11

Практичне заняття №4 Тема: Формула Тейлора. Обчислення границь за допомогою формули Тейлора. 13

Лекція №2 Дослідження на монотонність та екстремуми. Випуклі функції. Правило Лопіталя. 15

Практичне заняття №5 Тема: Правило Лопіталя. Використання похідної для розв’язання рівнянь, нерівностей, доведення нерівностей. 19

Практичне заняття №6 Тема: Використання похідної для розв’язання рівнянь, доведення тотожностей, розв’язання задач на мінімаксимум. 21

Практичне заняття №7 Тема: Дослідження функцій. 23

Диференціальне числення відображень 25

Лекція №3 Лінійний нормований простір з скалярним добутком. Лінійні оператори 25

Практичне заняття №8 Тема: Лінійний нормований простір зі скалярним добутком. Лінійні оператори. 30

Лекція №4 Похідна у напрямку. Частинні похідні. Повна похідна. 32

Практичне заняття №9 Тема: Частинні похідні. Похідна у напрямку. Повна похідна. 37

Лекція №5 Геометрична інтерпретація похідної відображення. Градієнт. 39

Практичне заняття №10 Тема: Геометричний зміст похідної функції. Механічний зміст похідної. 42

Лекція №6 Диференціал. Загальні закони диференціювання 44

Практичне заняття №11 Тема: Диференціал функції. Загальні закони диференціювання. 46

Лекція №7 Формула скінчених приростів 48

Лекція №8 Похідні вищих порядків. Формула Тейлора. 51

Практичне заняття №12 Тема: Похідна та диференціал вищого порядку. Формула Тейлора. 55

Лекція №9 Дослідження внутрішніх екстремумів. Дослідження екстремумів у випадку функцій двох змінних 57

Практичне заняття №13 Тема: Дослідження екстремумів у випадку функцій кількох змінних. 60

Лекція №10 Теорема про неявну функцію 61

Лекція №11 Умовні екстремуми 65

Практичне заняття №14 Тема: Умовні локальні екстремуми. 69

Література 70

Передмова

Пропонований посібник призначений для студентів фізико-математичного факультету спеціальності «Математика», а також може використовуватися студентами суміжних спеціальностей, у яких читається курс математичного аналізу.

Як і в першій частині, виклад матеріальну широко використовує елементи функціонального аналізу, що спрощує доведення властивостей. Факти, що стосуються більш конкретної ситуації формулюються у вигляді прикладів .

Зазначимо, що ряд властивостей не доводяться, це стосується тих тверджень, які не важко знайти у загальнодоступній літературі, або довести самостійно у якості вправи.

Як і в першій частині, протягом всього посібника лекції передуються з практичними заняттями. В кінці наводиться список літератури по теорії та практиці в сполученні з якими, ми сподіваємося, даний посібник допоможе засвоїти предмет більш глибше.

Лекція №1 Похідна функції однієї змінної. Властивості.

Нижче ми розглянемо означення та властивості похідної для функції однієї змінної. Однак, практично всі властивості приводяться без доведень (які можна легко знайти в книгах .1, 2.), з однієї сторони, оскільки їх не важко знайти та розібратися самостійно, а з іншої, оскільки подібні факти будуть доведенні нижче в більш загальній ситуації.

1. Похідна, диференціювання та їх зв’язок.

Нехай .

Означення. Функція називається диференційованою в точці ( - гранична для Е), якщо існує лінійна відносно приросту аргументу функція , що , де - нескінченно мала більш високого порядку ніж при .

Означення. Лінійна функція називається диференціалом в .

Позначимо диференціал .

Нижче приріст аргументу у диференціалі функції будемо позначати , тобто .

Означення. Величина називається похідною в точці , якщо існує границя.

Приклад. 1. , 2. , (перевірити самостійно)

3. , 4. .

Теорема. Для того, щоб функція була диференційована в точці необхідно і достатньо, щоб вона мала в цій точці похідну.

Доведення. Якщо функція диференційована в точці , то

Достатню умову довести самостійно. Також з цієї теореми маємо .

Теорема. Якщо диференційована в точці , то вона і неперервна в цій точці.

Зазначимо, що обернене твердження невірне.

Наприклад. неперервна в , але не диференційована (довести застосовуючи означення похідної).

2. Основні властивості диференційованих функцій.

Доведення приведених нижче властивостей знайдіть та вивчіть самостійно [см літературу 1, 2]

1. Якщо функції і диференційовані в точці , то диференційовані і їх похідні дорівнюють відповідно .

Приклад. 1. (довести за допомогою математичної індукції).

2. (застосувати властивість 1)

2. Якщо функція диференційована в точці , а функція диференційована в точці 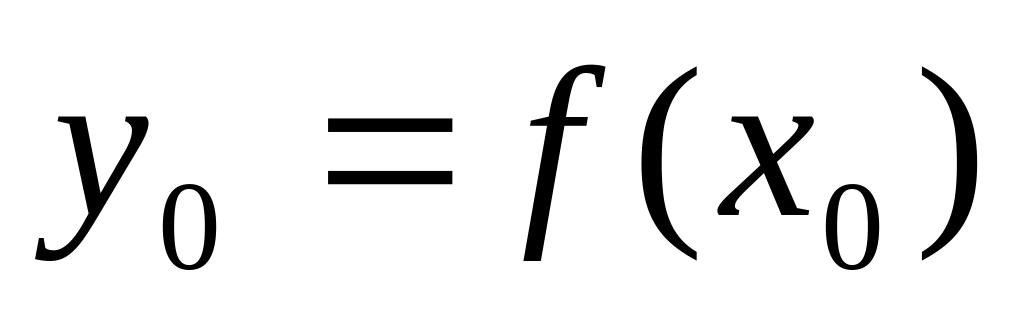, то складена функція диференційована в точці , та (де похідна зовнішньої функції береться по проміжному аргументу ).

3. Якщо функція має обернену та диференційована в точці і , то обернена функція диференційована у точці , та виконується рівність

Приклад. 1.

2. , (застосувати властивість 3 та похідні функцій ).

З властивостей 1-3 для похідних випливають відповідні властивості диференціалів функцій.

1.

2. Якщо та диференційована в точці , то незалежно від того являється незалежною зміною, або функцією , диференціал має вигляд , причому якщо - незалежна змінна, то незалежний приріст аргументу, а якщо функція, то - диференціал цієї функції.