Часть III. Внешнее ориентирование фотограмметрической сети

Целью этого процесса является переход от фотограмметрических координат точек местности к геодезическим.

Если маршруты короткие и строятся по крупномасштабным снимкам, то при внешнем ориентировании координаты опорных точек можно иметь в гауссовой системе.

В аналитическом способе сначала определяют элементы внешнего ориентирования модели сети, после чего от координат точек в фотограмметрической системе переходят к их значениям в принятой системе координат X_GY_GZ_G.

Элементами внешнего ориентирования являются:

• t – знаменатель масштаба модели;

• X₀, Y₀, Z₀ – геодезические координаты начала фотограмметрической системы координат;

• ζ – продольный угол наклона модели;

• η – поперечный угол наклона модели;

• θ – угол поворота модели.

Связь между координатами точки в системе X_GY_GZ_G и в фотограмметрической системе X_FY_FZ_F выражается формулами

(42)

где ΔX_F, ΔY_F, ΔZ_F – приращения координат определяемой точки относительно начала координат; a_i, b_i, c_i – направляющие косинусы, вычисляемые по формулам

. (43)

Подставляя в формулы (42) значения направляющих косинусов из (43) и принимая t = t₀+δt, X₀ = X₀”+δX₀, Y₀ = Y₀”+δY₀, Z₀ = Z₀”+δZ₀, получим

(44)

где

(45)

Уравнения (44) являются строгими.

Одна опорная точка дает возможность составить три уравнения (44) с семью неизвестными. Поэтому для внешнего ориентирования модели необходимо не менее трех опорных точек, из которых две должны иметь все три координаты, а третья – только Z. При избыточном числе точек задачу решают по методу наименьших квадратов.

Так как в коэффициенты при неизвестных и свободный член входят определяемые неизвестные, то задача решается методом последовательных приближений. В первую очередь, используя приближенные значения неизвестных, по формулам (43) вычисляют направляющие косинусы, затем по формулам (42) находят ΔX_F, ΔY_F, ΔZ_F и по формулам (45) – коэффициенты и свободные члены. От уравнений поправок переходят к нормальным уравнениям. Из их решения определяют неизвестные в первом приближении. Используя результаты первого приближения, находят коэффициенты и свободные члены для второго приближения и т.д.

Решение задачи упрощают следующим образом. Сначала определяют знаменатель масштаба модели, используя формулу

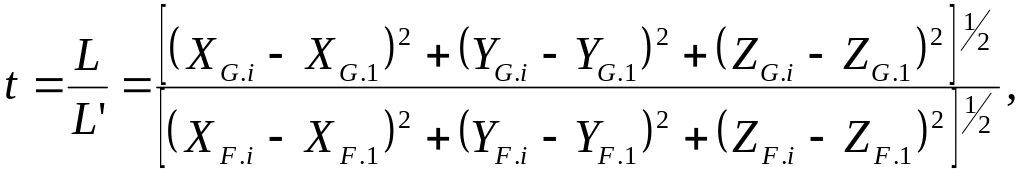(46)

где L, L’ – расстояние между точками на местности и на модели соответственно. Так как имеются избыточные данные, то значение t вычисляют как среднее весовое, т.е.

(47)

В качестве веса принимают величину .

После преобразований имеем

(48)

где

(49)

Уравнения (49) являются строгими. Их целесообразно решать следующим образом: сначала составить третье уравнение для всех опорных точек и из их решения найти значения tgζ и tgη, а затем из первого и второго уравнений, также составленных для всех опорных точек, вычислить sinθ.

После определения величин ζ, η, θ по формулам (43) находят направляющие косинусы, а затем по формулам (42) – координаты X₀, Y₀, Z₀ начала фотограмметрической системы. Определив элементы внешнего ориентирования, по формулам (42) вычисляют координаты всех точек сети сгущения в гауссовой системе координат.

ЛИТЕРАТУРА

1. Куштин И.Ф., Бруевич П.Н., Лысков Г.А. Справочник техника-фотограмметриста. – М.: «Недра», 1988.

2. Лобанов А.Н., Овсянников Р.П, Дубиновский В.Б. Фототриангуляция с применением электронной цифровой вычислительной машины. – М.: «Недра», 1967.

3. Лобанов А.Н. Фотограмметрия. – М.: «Недра», 1984.