
- •Основные свойства числовых систем
- •4 В области n непосредственно следует за 3. 4 в области n не является непосредственно следую-щим за 2, так как имеется число 3 (3 из n), которое лежит между 2 и 4.
- •2, Аксиоматическпй подход к изучению натуральных чисел
- •Переместительных свойств:
- •4.Десятичное измерение отрезка и появление действительных чисел
- •Можно представить числа на схеме
- •Свойства числовой области относительно порядка
- •5.Арифметические действия над разными числами их свойства
- •Порядок действий в вычислительных операциях
- •6.Целые неотрицательные числа и отношение делимости
- •7. Дроби и операции над ними
- •Арифметические операции с конечными десятичными дробями
- •Преобразование форм представления дробных чисел
- •Положительные и отрицательные чис '
- •Можно представить числа на схеме
- •Применение приближённых вычислений
- •2. Уравнение и его решение.
- •3.Неравенство с переменной и его решение.
- •Основные понятия математической статистики
- •2.График кривой Гаусса симметричен относительно
- •3.Симметричность и вытянутость графика, а значит
- •55554444444333333332 До эксперимента
- •55545544345444433333 После эксперимента
- •1) Наличие матрицы (таблицы) не меньше 3-го порядка;
- •2) Все коэффициенты корреляции положительные;
- •3) Все коэффициенты коррел. Статистически значимые.
- •1) Наличие матрицы (таблицы) не меньше 3-го порядка;
- •2) Все коэффициенты корреляции положительные;
- •3) Все коэффициенты коррел. Статистически значимые.
- •Качалко,в.Б. Поисково-исследовательская технология начального обучения математике /в.Б. Качалко.–Мозырь: мгпу им. И.П. Шамякина, --2008.-142с.
- •Тематика докладов и их содержание по методике обучения младших щкольников решению задач
- •З простай і састаўной задачамі
- •5 І 4 лікавыя дадзеныя задачы
- •3. Да састаўленых задач падабраць патрэбныя выразы:
- •Решение:
- •Синтетический способ
- •Рассуждаем по схеме:
- •1) Как результат, ответ на вопрос задачи;
- •2) Как процесс нахождения этого результата;
- •3) Как перечень тех действий, которые
- •3) (27: 3) – 3 – Было тетрадей у Алеся
- •1 2 3 4 5 6 7 8 1 2 3 4 5 Пабудаваць дыяграму працягласці жыцця людзей:
- •1. Іваноў-10г. 2.Пятроў –30г. 3.Сідараў-50г.
- •4. Радзімаў-40г. 5.Антонаў -20г.
- •1. Паўтарэнне нумарацыі 3-х і чатырохзначных лікаў.
- •2. Выкарыстанне лічыльнікаў: паказ, дзе, на якім дроціку адкладваюцца адз. Тыс., дзес. Тыс., сотні тысяч.
- •3. Прымяненне табліцы разрадаў і класаў:
- •5. Складанне і адніманне найменных лікаў праводзіцца пасля папярэдняга прадстаўлення іх ў аднолькавых най-меннях і выконвацца так, як і над абстрактнымі лікамі:
- •6. Складанне і адніманне найменных лікаў у прасцей-шых выпадках без прадстаўлення лікаў ў аднолькавых мерах: 5км 750м
- •1. Увядзенне тэарэтычнай асновы дзялення:
- •3. Множанне ліку з нулямі ў канцы запісу: 189 000
- •5. Пісьмовае множанне найменных лікаў:
- •6. Множанне многазначнага на трохзначны лік
- •7. Множанне многазначных лікаў з нулямі ў сярэдзіне і канцы: 829 8290 6700
- •Основы математической статистики
- •Содержание
- •Содержание
- •Самостоятельная работа 1
- •Оценки результатов учебной деятельности младших школьников по математике
- •Литература
- •Аналитический способ поиска
- •Синтетический способ поиска
- •Поиск способа решения текстовой задачи методом дополнения
- •Переформулировка задачи
- •К раткая запись
- •Алгебраический способ решения
- •Геометрический способ решения
- •У Алеся у Миши у Лёни
- •Дополнительные способы работы над задачей
- •За курс начальных классов
- •Литература основная
- •Дополнительная
Можно представить числа на схеме
Действительные числа R
Р ациональные ч Q + Q- Иррациональн ч. I
Целые числа Z Дробные числа Q+
Отрицательные Z_ Натуральные N.
целые числа числа и число 0.
Применение приближённых вычислений
Для этого разработаны рекомендации.
1.Вводится понятие значащее цифры прибли-женного числа, все цифры которого отличные от нуля, и все нули, если они содержатся между значащими цифрами или являюся представи-телями сохранённого разряда (в конце дроби).
2.Чтобы округлить число с точностью до указанного разряда, нужно цифры, стоящие правее этого разряда, отбросить в дробной части числа или заменить нулями в целой части числа. Последняя сохраняемая цифра округляется по правилам округления:
2.1.Если первая отбрасываемая цифра больше пяти, то в последнем сохраняемом разряде цифра увеличивается на единицу.
2.2.Если первая отбрасываемая цифра пять и за ней есть ещё цифры, отличные от нуля то в последнем сохраняемом разряде цифра увеличивается на единицу.
2.3.Если первая отбрасываемая цифра пять и за ней больше никаких цифр за исключением нулей, то последнюю сохраняемую цифру оставляют без изменения, если она чётная; увеличивают на единицу, если она нечётная.
3.Чтобы найти сумму нескольких приближённых чисел с точностью для целой или дробной единицы какого-либо разряда, если слагаемых меньше 10, надо взять каждое число с числом десятичных знаков на один больше, чем у дроби приближения, сложить их, в полученной сумме отбросить последнюю цифру и увеличить на единицу предпоследнюю цифру.Если слагаемых более 10, но менее 100,то нужно взять каждое из них с числом десятичных знаков на два больше, чем в дроби с наименьшим приближением сложить их, в полученной сумме отбросить две последние цифры и прибавить единицу к последней удержанной цифре; полученное число есть искомая сумма с заданной точностью.
4. Чтобы найти разность двух приближённых чисел с точностью для целой или дробной единицы какого-либо раз-ряда, надо в уменьшаемом и вычитаемом обросить все циф-ры, стоящие справа от той, которая выражает единицу разряда степени точности; затем найти разность полученных чисел
5.При сложении и вычитании приближённых чисел в результате следует сохранять столько десятичных знаков, сколько их в приближённом числе с наименьшим числом десятичных знаков.
6.При сложении и вычитании приближённых чисел в результате следует сохранять столько десятичных знаков, сколько их в приближённом числе с наименьшим числом десятичных знаков.
7. При умножении и делении приближённых чисел в результате следует сохранять столько значащих цифр, сколько их имеет наименее точное из данных чисел. Из нескольких приближённых чисел наименее точным считается то, которое имеет наименьшее количество верных значащих цифр.
8.При возведении в квадрат и куб приближённых чисел результате следует сохранять столько значащих цифр, сколько их имеет основание степени.
9. При извлечении квадратичногог и кубического корня следует сохранять столько же значащих цифр, сколько их имеет подкоренное число.
10. При вычислении промежуточных результатов следует сохранить одну лишнюю запасную цифру, которую в окончательном результате надо отбросить.
![]()
План
Структура эксперимента с применением математической статистики.
Статистические гипотезы и способы их проверки.
Критерии Фридмана и Стьюдента.
Приближённе вычисления.
Ключевые компетенции: структура эксперимента, .
Литература
Качалко, В. Б. Методы психолого-педагогических исследований с применением математической статистики /В. Б.Качалко. –Мозырь: МГПУ им,И.П, Шамякина, 2008.—142 с. Глава 3.
1. СТРУКТУРА СРАВНИТЕЛЬНОГО ЭКСПЕРИМЕНТА
При проведении исследований основнвм методом является сравнительный эсперимент, который про-водится по следующей схеме на эквивалентных экспеимертальной и контрольной группах.
Выбор, уравнивание классов |
Экспе-римен-таль-ные клас-сы |
Учебная работа с введением новоо фактора |
Учеб-ная работа без нового фак-тора |
Кон-трольные клас-сы |
|
||
|
|
|
|||||
|
|
|
|||||
Определение начального уровня ЗУНов уч-ся по исследуе-мым вопросам |
Нэ |
|
|
Нк |
|
||
|
|
|
|||||
Эксперимент |
|
|
|
|
|
||
Определение ЗУНов в конце эксп. |
Кэ |
|
|
Кк |
|
||
|
|
|
|||||
Прирост знаний. |
|
|
Кк-НкПк |
|
|
|
|
6.Эффектив-ность эксп.
|
|
|
|
|
|
||
П Пэ-Пк |
|
||||||
|
|
||||||
При сравнительном эксперименте необходимо:
1. Уравнять условия учебной работы, кроме экспериментального фактора, в эксперимен-тальных и контрольных классах (группах).
2.Определить путём тестирования начальный уровень знаний, умений и навыков, развития учащихся экс- периментальных и контрольных классов (Нэ и Нк).
3.Провести учебную работу в экспериментальных классах с введением экспериментального фактора, а в контрольных классах без него.
4.Снова
определить
уровень знаний, умений и навыков, развития
после
эксперимента(Кэ,Кк).

5. В обоих случаях вычесть из средних показателей окончательных знаний средний показатель начальных знаний, умений и навыков учащихся экспериментальных и контролных групп (Кэ-НэПэ, Кк-НкПк).
6.Разности покажут прирост знаний, умений и навыков и развития в экспериментальных и контрольных классах
7.Вычислить сравнительную эффективность экспери-ментального фактора (Пэ-Пк) с применением анализа статистическими методами, который покажет эффек-тивность влияния нового фактора на учебный процесс .
Этот вид эксперимента является наиболее пригод-ным для исследований в школе.
2.Статистическая гипотеза-
это предположение, которое необходимо доказать с помощью критериев статитических с установленной достоверностью не менее 95% для психолого-педагогических исследований, с уровнем значимости 5%, или в десятичных дробях с достовенрн. 0,95 и уровнем значимости 0,05.
Уровень
значимости – это вероятность отклонения
нулевой
гипотезы о
том, что распределения не различаются,
При отклонении нулевой гипотезы
принимается
альтернативная гипотеза,
что распределения отличаются.
Статистическую гипотезу в отличие от
научной никогда не можно полностью
доказать, но всегда можно отклонить.
Ошибка
отклонения
верной статистической гипотезы не
должна превышать 5%. Она называется
уровнем
значимости, который обозначается
р![]() 5%
или р
0,05.
Достоверность
принятия
верной статистической гипотезы тогда
будет не менее 95% или 0,95.
5%
или р
0,05.
Достоверность
принятия
верной статистической гипотезы тогда
будет не менее 95% или 0,95.
В статистике вводится понятие степени свободы, которое всегда меньше на 1 числа опытов. Потому для каждой из выборок с количеством элементов п1 и п2 число степеней свободы будет соответствовать п1 - 1 и п2 - 1, а вместе (п1-1)+(п2-1)=п1+п2-2.
Для проверки статистических гипотез учёными составлены таблицы критических значений для каждого статистического критерия с учётом степеней свободы и уровня значимости : р=5% (достоверность 95%), р=1% (достоверность 99%) .
Общий порядок проверки статистических гипотез:
формулируется основная (проверяемая) и альтернативная гипотезы;
выбирается статистический критерий для проверки справедливости гипотезы;
определяется уровень значимости (достоверности) принятия гипотезы , а затем табличное значение критерия;
проводится исследование, по результатам которого расчитывается фактическое значение критерия;
на основе сравнения фактического и критического знач. делается вывод о правдоподобности или необходимости отклонения выдвинутой гипотезы.
Для принятия гипотезы требуется, чтобы вычисленное значение было не меньше табличного. Таблицы критических значений имеются у каждого из вас, правила их использования разрабатываются для каждого критерия.
![]()
Для проверки статистических гипотез при-меняются критерии Фишера (F) и Стьюдента (t).
Если вычисленное по формуле кри-терия значение равно или больше таблич-ного, то утверждают, что гипотеза подт-
вердилась с достоверностью не ниже 95% .
Критерий Фишера определятся по формуле:
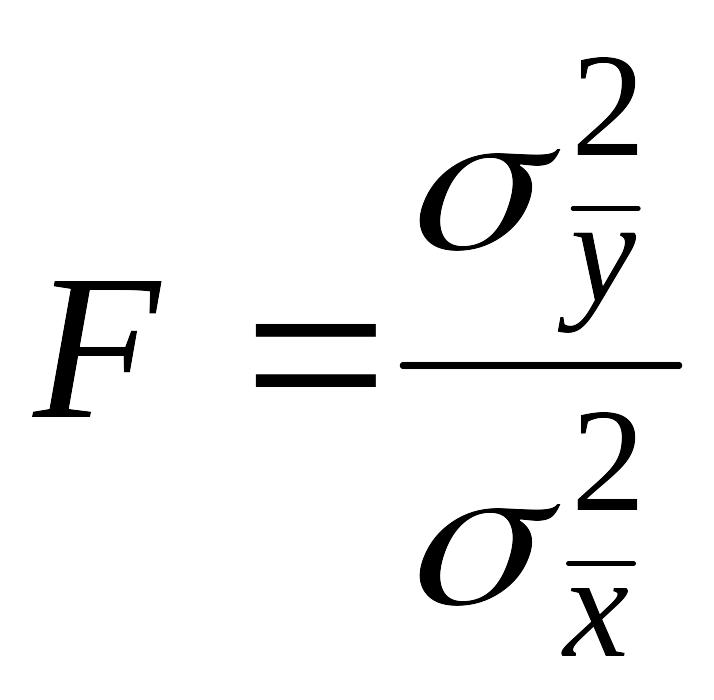 или
наоборот,
чтобы
большая
дисперсия делится на меньшую, поэтому
всегда F
или
наоборот,
чтобы
большая
дисперсия делится на меньшую, поэтому
всегда F![]() 1.
1.
Критическое значение критерия F находится по таблице для п1–1 и п2–1 степеней свободы, где п1 и п2 количество испытуемых в контрольной и экспериментальной группах. Для нашего случая F=3,1:2,7=1,15 при п1-1=10-1=9 и п2–1=10-1=9 степенях свободы. На пересечении указанных строк и столбцов находим по таблице критических значений критерия F для достоверности 95% значение 3,18. Так как 1,15 меньше 3,18, принимается ну-левая гипотеза, различие несуществен-ное между распределениями,то экспе- иментальная гипотеза отклоняется.
Критерий Стьюдента t вычисляется по
формуле:
 ,
где
,
где
![]() и
и
![]() ,
,
![]() и
и
![]() -
соответствующие параметры кон-трольной
и экспериментальной групп, а п1
и п2
– количество испытуемых
в этих группах.
-
соответствующие параметры кон-трольной
и экспериментальной групп, а п1
и п2
– количество испытуемых
в этих группах.
Для
нашего случая имеем
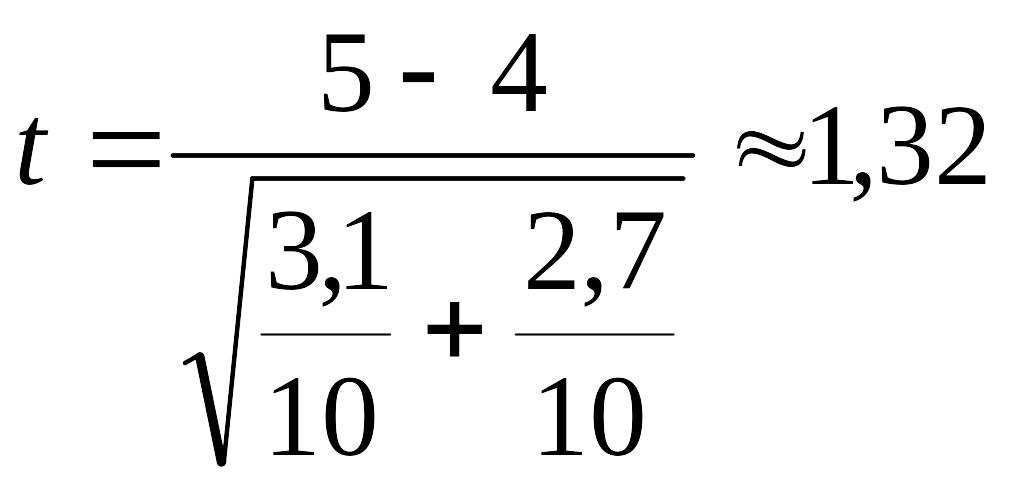
Далее находим критическое значение по таблице критерия t для достоверности 95% и п1 + п2 – 2 = 10 + 10–2 =18 степеней свободы. Оно равно 2,1. Так как 1,32 меньше 2,1, принимается нулевая гипотеза меньше 2,1, различие между выборками несущественное то экспериментальная гипотеза не подтвердилась.
Для повторных измерений на одной и той же выборке испытуемых применяется другая формула критерия Стьюдента:
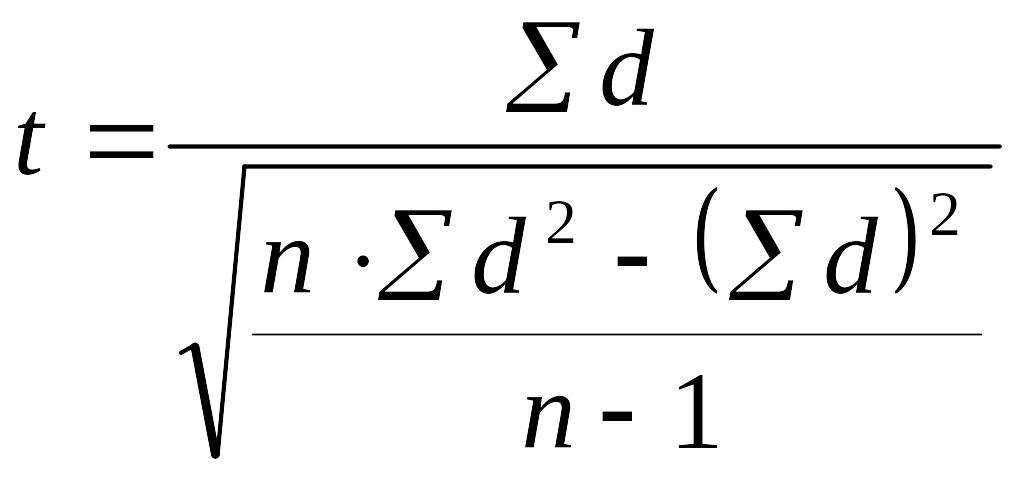 ,
где
,
где
d – разность между данными каждой пары;
d – сумма разностей с учетом знаков;
(d)2 – квадрат суммы разностей; n – число пар испытуемых.
Эта формула применяется в основном на одних и тех же испытуемыхю
Результат исследования проверяется по таблицам критических значений для п-1 = степеней свободы для установления достоверности различия не меньше 95%, или не больше 5% уровня значимости.
ПРИМЕНЕНИЕМ ПРИБЛИЖЁННЫХ ВЫЧИСЛЕНИЙ
При проведении научных исследований приходится измерять разный материал, получая при этом числовые данные с заданной точностью.
1.Чтобы округлить число с точностью до указанного разряда, нужно цифры, стоящие правее этого разряда, отбросить в дробной части числа или заменить нулями в целой части числа Последняя сохраняемая цифра округляется по правилам округления:
2.1.Если первая отбрасываемая цифра больше пяти, то в последнем сохраняемом разряде цифра увеличивается на единицу: 2126 ≈ 2 130 (до десятков)
2.2.Если первая отбрасываемая цифра 5 и за ней есть ещё цифры, отличные от нуля то в последнем сохраняемом разряде цифра увеличивается на единицу.
2.3.Если первая отбрасываемая цифра 5 и за ней больше никаких цифр за исключением нулей, то пос-леднюю сохраняемую цифру оставляют без изменения, если она чётная; увеличивают на единицу, если она нечётная.: 21, 265007 ≈21,26; 21, 275008 ≈21,28.
3.При сложении и вычитании приближённых чисел в результате следует сохранять столько десятичных зна-ков, сколько их в приближённом числе с наименьшим числом десятичных знаков.
4. При умножении и делении приближённых чисел в результате следует сохранять столько значащих цифр, сколько их имеет наименее точное из данных чисел.
5.При вычислении промежуточных результатов следует сохранить одну лишнюю запасную цифру, которую в окончательном результате надо отбросить.
УРАВНЕНИЯ,
НЕРАВЕНТСТВА И ИХ СВОЙСТВА
План
Числовые выражения и выражения с
переменной.
2. Числовые равенства и неравенства и их
преобразования.
3. Уравнения и их решение.
4. Неравенства с переменной и их решение.
Ключевые компетенции: математический алфавит, математические выражения, равенства и неравен-ства. уравнения и неравенства с переменной.
Основная: [1,гл.5][2, гл. 5] [3,гл. 7]
Дополнительная : [4,гл.7 ]
Математические выражения.
Любая наука пользуется своим языком: предложениями, словами-терминами, символами (специальными знаками) .
Алфавит математики состоит из 33 букв русского языка, цифр и специальных терминов. Разработаны правила составления из букв и других символов мате-матических выражений, имеющих смысл. Берутся ма-лые и большие буквы латинского алфавита и цифры. соединяются знаками арифметических действий в выражения. Например: 1) 2+3; 2) х+5=7; 3) х+ 5 >∞ явля-ются выражениями: первое --числовым , второе выра-жением с переменной (уравнение), третье—вообще не имеет смысла. Числовые выражения конструюруются из цифр 0,1,2,3,4,5,6,7, 8,9, знаков арифметических действий +, - , х, : из скобок (),{}, []. Цифра также выражение, а знаки действий и скобки—нет.
Два числовых выражения, соединёппые знаком «=»: а=в называются числовыми равенствами. 5+1=3+2 и 5+1=4+3 -- примеры числовых равенств. Однако первое равенство истинное, а второе - ложное. Аналогично два числовых выражения, соединёппые знаком
«>» или «>»: называются числовыми неравенствами: 5+1 < 3 и 5+1 > 2+1- примеры числовых неравенств. Однако первое равенство ложное, а второе – истиное.
Основные свойства числовых равенств: 1. Если к обеим частям истинного числового равенства прибавить одно и то же числовое выражение, имеющее смысл, то получим так-же истинное числовое равенство.
2. Если обе части истинного числового равен-ства умножить на одно и то же числовое вы-ражение, имеющее смысл, то получим так-же истинное числовое равенство.
Аналогичные свойства числовых неравенств:
1. Если к обеим частям истинного числового неравенства прибавить одно и то же числовое выражение, имеющее смысл, то получим также истинное числовое неравен-ство.
2. Если обе части истинного числового равен-ства умножить на одно и то же числовое выражение, имеющее смысл и принимающее положительное значение , то получим так-же истинное числовое неравенство.
3. Если обе части истинного числового неравенства умножить на одно и то же чис-ловое выражение, имеющее смысл и принима-ющее отрицательное значение, то чтобы получить истинное числовое неравенство необходимо знак неравенства поменять на противоположный.
Возьмём два выражения с переменной
5(х+1) и 5х+5. Областью их определения является множество действительных чисел. Составим таблицу, вычислим
Х |
5(х+1) |
5х+5 |
2 |
10 |
10 |
- 3 |
- 20 |
- 20 |
2,4 |
17 |
17 |
В выражениях можно выполнять все допустимые действия.
О1. Два выражения тождественно равны, если при любыз значениях переменных из области определения выражений их соответ-вующие значения равны.

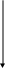



 Кэ-Нэ
=Пэ
Кэ-Нэ
=Пэ