Самостоятельная работа 1

1. Для проверки памяти 25 учащимся предложили воспроизвести слова текста. Получили ряд:

9, 8, 11, 7, 9, 10, 6, 8, 4, 7, 5, 8, 12, 5, 7, 9, 6, 10, 6, 8, 10, 7, 9, 8, 11

Составить статистическое распределение по форме

Количество слов	12	11	10	9	8	7	6	5	4
Количество учащихся (частота fi )

2. По данному распределению построить график (полигон)

3. Записать данные задания 1 в интервальную таблицу по форме

Интервалы Количество испытуемых (f_i)

10. ______

7. ______

4. ______

4. По заданию 3 построить столбиковую диаграмму (гистограмму).

5. Определить моду, медиану, среднее арифметическое. Будет ли полученное распределение нормальным?

6. По значению 1 заполнить таблицу по форме

Кол. слов xi	Част. fi	Лин. откл.	Модуль отклонения		Квадратичное отклонение

7. Вычислить среднее линейное отклонение.

8. Вычислить среднее квадратичное отклонение (дисперсию) для n<30, стандартное отклонение.

9. Найти доверительные границы среднего арифметического.

10. Вычислить коэффициенты вариации.

Самостоятельная работа 2

1. Составить таблицу по форме, где x_i- отметки контрольной и y_i- экспериментальной группы

xi	yi
1	2	3	4	5	6	7
9	10
7	9
6	8
6	8
5	6
5	6
5	6
4	5
4	5
4	4
3	3
2	2

Σ= Σ= Σ= Σ= Σ=

2. По таблице найти М_о, М_е, . Установить, будут ли распределения нормальными.

3. Вычислить критерий Фишера F.

4. Вычислить критерий Стьюдента t. Определить, оправдался ли эксперимент.

5. Вычислить коэффициенты вариации V_x и V_y.

6. Найти коэффициент линейной корреляции Пірсона. Существует ли взаимосвязь между отметками двух групп?

7. Составить уравнения линейной регрессии и начертить их графики.

8. В выборке из 6 учеников измерили развитие логического мышления до эксперимента (x_i) и после него(y_i). Установить, существенно ли улучшилось логическое развитие. Заполнить таблицу

xi	yi	yi-xi=d
1	2	3	4
4	9	5
3	8	5
3	7	4
3	7	4
2	6	4
2	5	3

Самостоятельная работа 3

1. Установить по критерию знаков Z, подтвердилась ли гипотеза, если в классе учениками были получены отметки:

до эксперимента 5555544444443333323333322

после эксперимента 5455545344453444433442432

Знаки «+», «-», «0».

2. По критерию Пирсона определить, подтвердился ли эксперимент, если учащимися получены отметки до эксперимента (x_i), после эксперимента (y_i)

   Отметки	xi	yi			- %	( - )2
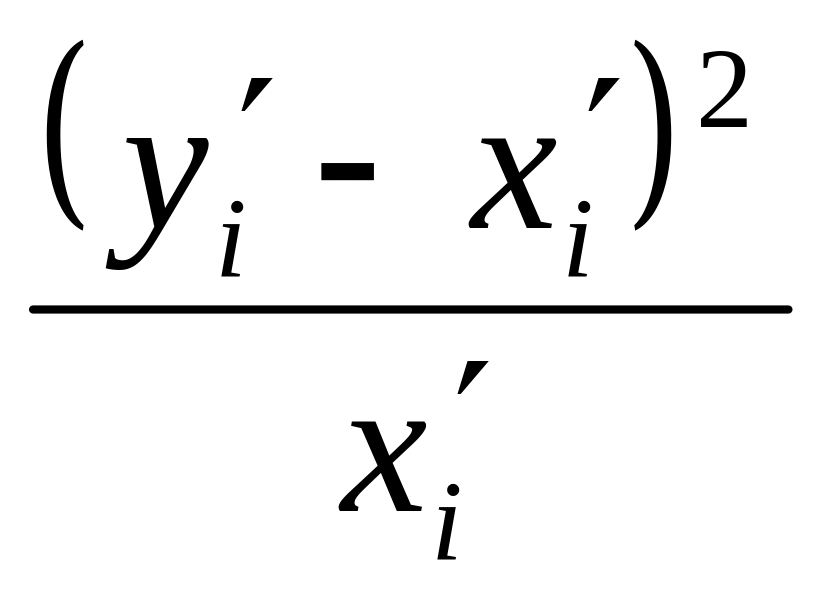
   1	2	3	4	5	6	7	8
   «Пять»	5	6
   «Четыре»	12	13
   «Три» и «два»	8	7

3. После эксперимента проанкетировали 30 учащихся. Необходимо ответить на вопрос : «Любите ли вы решать нестандартные задачи?» (да, нет). По критерию установить, существенно ли повысился интерес, если ответили «да» - 20 учеников, «нет» - 10 учащихся. Предварительно составить таблицу.

4. По критерию ранговой корреляции Спирмена (ρ) определить, существует ли значимая корреляция между знаниями учащихся по белорусскому и русскому языку. Оценки получены по 10-балльной шкале. Предварительно заполнить таблицу.

Бел. язык xi	Ранги xi	Рус. язык yi	Ранги yi	Разность рангов yi-xi=d	Квадрат разности рангов (yi-xi)2=d2
1	2	3	4	5	6
10		10
10		9
9		9
9		8
9		8
8		8
7		7
6		6
5		4
5		5

Σ= Σ=

5. В результате эксперимента были получены интеркорреляции, занесенные в таблицу по трём сериям задач:

• с несформулированным вопросом (1),

• с недостающими данными (2),

• с излишними данными (3).

Серия	1	2	3
1	-	0.64	0.72
2	0.67	-	0.67
3	0.72	0.67	-

Установить, можно ли объяснить решение всех трёх серий задач действием общего фактора

ДЕСЯТИБАЛЛЬНАЯ ШКАЛА