1 2 3 4 5 6 7 8 1 2 3 4 5 Пабудаваць дыяграму працягласці жыцця людзей:

1. Іваноў-10г. 2.Пятроў –30г. 3.Сідараў-50г.

4. Радзімаў-40г. 5.Антонаў -20г.

На ўроках матэматыкі дзеці вучацца рабіць геаметрычныя пабудаванні звычайна па такому плану:

аналіз пабудаванне доказ даследаванне.

Напрыклад: Пабудаваць прамавугольнік, сума даўжынь старон (перыметр) якога роўная 12 см.

Даўжыня 5 4 3

Шырыня 1 2 3 Аналіз ідзе па табліцы

Перыметр 12 12 12

Даследаванне: вучні ўстанаўліваюць,што існуюць толькі тры розныя прамавугольнікі. Адзін з прамавугольнікаў – квадрат. Далей ідзе пабудаванне прамавугольнікаў знойдзеных памераў: 3 см

5 см 4 см

1см 2см 3 см

В программе для начальных классов наибольшее внимание уделяется представлениям о прямоугольнике, треугольнике, квадрате и круге. . Геометрические фигуры используются для счёта, для классификации по ве-личине, форме,цвету, треугольников по углам, сторонам

Отводится время на построение геометрических фигур и диаграмм сначала на бумаге в клеточку, затем в прямоугольной системе координат: А (1;3),В(2;8)

.…

10			О			F			C
9
8	В
7
6		К			М	E			D
5
4			N
3 А					S	R
2		L
1				P			U		X

0 1 2 3 4 5 6 7 8 9 10

ГЕОМЕТРИЧЕСКИЕ ПРЕДСТВЛЕНИЯ УЧ-СЯ НАЧАЛЬНЫХ КЛАССОВ

150
140
130
120
110
100

0 1 2 3 4 5 6 7 8 9 Учащиеся знакомятся с диаграммами и некоторыми геометрическими фигурами, способами их получения.

П РИЗМА - тело, у которог о верхняя и нижняя грань – равные многоугольники, а боковые грани прямоугольники.

ПАРАЛЛЕПИПЕД − призма,грани у которой прямоугольники.

c ²

a²

b² S=2a²+2b²+2c²

Вычисляют сначала площадь его развёртки,а затем темобъём параллепи педа V= a•b•c. КУБ - это параллелепипед, у которого все грани – квадраты

Также сначала вычисляю площадь

S=6•a² поверхности, затем объём

куба V= a³ .

ПИРАМИДА строится на основании многоугольника. Выбирается точка,лежащая выше основания вершины многоугольника, которые соединятся с этой точкой −вершиной пирамиды.

Если вращать круг вокруг прямой линии, прохо-

ей через его центр,то круг опишет шар.Е сли вращать прямоугольник вокруг

его стороны, то он опишет ЦИЛИНДР.

Е 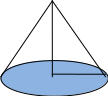сли вращать прямоугольный треугольник вокруг стороны, которая прилегает к прямому углу, то прямоуголь0-ник опишет КОНУС. Его развёрткой будет

круг и треугольник.

Т АКИМ ОБРАЗОМ, УЧАЩИЕСЯ НАЧАЛЬНЫХ КЛАССОВ ЗНАКОМЯТСЯ СО СВОЙСТВАМИ И ПОСТРОЕНИЕМ НЕКОТОРЫХ ГЕОМЕТРИЧЕСКИХ ФИГУР НА ПЛОСКОСТИ И ПРОСТРАНСТВЕ

Разбор геаметрычнай задачы выконваецца па схеме:

1. Засваенне ўмовы і пытання (патрабавання) задачы:

чытанне тэксту; выясненне, што абазначае кожнае лікавае дадзенае, адносіна , сувязь; устанаўленне, ці хапае дадзеных або маюцца лішнія дадзеныя для рашэння задачы. Па чарцяжу патрэбна адказаць, што абазначае кожная лінія, вугал, фігура і т.д.

2.Мадэляванне задачы ў выглядзе: кароткага запісу, гра-фічнага малюнка, чарцяжа, граф-схемы, табліцы, схемы.

3. Пошук спосабу рашэння задачы. Рашэнне задачы рознымі спосабамі разбору:аналітычным ( ад пытання да дадзеных); сінтэтычным (ад дадзеных да пытання), аналітыка-сінтэтычным двух відаў. Успамінаюць розныя спосабы пабудавання геаметрычных фігур.

4. Рашэнне задачы з рознымі формамі запісу: па дзеяннях, складаннем выразу або ураўнення з запісамі тлумачэнняў да паслядоўных прамежкавых выразаў або без запісу іх.

5. Праверка рашэння: прыкідкай адказу; рашэннем задачы другім спосабам; састаўленнем і рашэннем адваротнай задачы; устанаўленнем адпаведнасці адказу ўмове задачы.

6. Рашэнне задачы іншымі спосабамі і выбар найбольш рацыянальнага з іх.

7. Даследаванне атрыманых рашэнняў і дадатковая работа над задачай. 8. Ацэнка хода рашэння задачы ў цэлым. Вызначэнне вучнем, аб чым ён даведаўся ў выніку рашэння задачы, дзе спатрэбяцца атрыманыя веды ў будучым

Больш поўны РАЗБОР ЛЮБОЙ ТЭКСТАВАЙ ЗАДАЧЫ звычайна выконваецца па схеме:

1.Засваенне ўмовы і пытання (патрабавання) задачы:

чытанне тэксту; выясненне, што абазначае кожнае лікавае дадзенае, адносіна і сувязь; устанаўленне, ці хапае дадзеных або маюцца лішнія дадзеныя для рашэння задачы; выдзяленне велічынь задачы і іх значэнняў, вядомых і шукаемых.

2.Інтэрпратацыя тэксту задачы ў выглядзе: кароткага запісу, графічнага малюнка, чарцяжа,, табліцы, схемы.

3.Пошук спосабу рашэння задачы. Пошук рашэння задачы рознымі спосабамі разважанняў:аналітычным (ад пытання да дадзеных); сінтэтычным (ад дадзеных да пытання), аналітыка-сінтэтычным спосабам двух відаў.

4.Рашэнне задачы з рознымі формамі запісу: па дзеяннях, складаннем выразу або ураўнення з запісамі тлумачэн-няў да прамежкавых выразаў або без запісу іх.

5.Праверка рашэння задачы розными спосабамі : прыкідка адказу; рашэннем задачы другім спосабам; састаўленнем і рашэннем адваротнай задачы; устанаў-леннем поўнай адпаведнасці адказу ўмове задачы. 6. Рашэнне задачы другімі спосабамі, аналіз спосабаў рашэння і выбар найбольш рацыянальнага з іх.

7.Дадатковая работа над задачай ( тэкстам і рашэннем).

8.Ацэнка хода рашэння задачы. Вызначэнне вучнем, аб чым ён даведаўся ў выніку рашэння задачы, якія цяж-касці сустрэў,які вопыт выкарыстаць ў будучым.

Застановімся на 5,6 і 7 этапах (на прыкладзе задачы)

5.1.Праверка прыкідкай адказу. Маса гарбуза 5кг,

што на 2кг больш масы дыні.Якая маса дыні? Падумай, ці больш важыць дыня за гарбуз. Чаму? 5-2=3(кг).

2. Праверка рашэннем адваротнай задачы: Дыня

важыць 3кг,а гарбуз 5кг. На колькі маса гарбуза больш масы дыні? На 5-3=2(кг) гарбуз цяжэй дыні.

5.3Праверка рашэннем задачы другім спосабам,

Гарбуз важыць 5кг, а дыня на 2кг менш. Колькі ва-жыць дыня? 5-х=2. Адкуль х= 5-2=5(кг)-маса гарбуза.

5.4.Устанаўленнем адпаведнасці паміж атрыманы-

мі лікамі і дадзенымі ўмовы задачы. Сапраўды атры-маная маса дыні 3кг на 5-3=2 (кг) меншая масы гар-буза , а маса гарбуза на 2кг большая масы дыні .

6.1..Найбольш рацыянальным можна прызнаць спосаб 5.3 на састаўленне ўраўнення па адносіне на 2кг менш.

Да дадатковых спосабаў работы можна аднесці: 7.1.Пераўтварэнне задачы з ускоснай формы ў прамую: Маса гарбуза 5кг, а дыні на 2кг менш. Якая маса дыні?

7.2.Параўнанне задач іх рашэнняў, Напрыклад, прапану-ецца параўнанаць тэкст і рашэнні папярэдніх задач з наступнай задачай:_ Маса гарбуза 5кг, а дыні на 2кг менш. Якая маса гарбуза і дыні разам? 5+(5−2)=8(кг).

7.3. Пераўтварэнне тэксту задачы з ускоснай формы у прамую форму (прыклад 5.3).

7.4.. Састаўленне задачы,адваротнай дадзенай (пр.5.2).

7.5.Замена аднаго з элементаў задачы другім (лікавых дадзеных, адносін,пытання,каб задача рашалася інакш).;

7 .6. Састаўленне задачы:

7.6.1 . Па кароткаму запісу: Г − 5кг, на 2кг больш − кг

Д − ?

7 .6.2. Па чарцяжу: !------5кг--------!—?кг------!

8кг

7 .6.3. Па рашэнню: 8−(5−2)=5 (кг)

7.6.4. Па табліцы:

7.6.5. Па схеме:

7.6.6. Па пытанню да задачыэ

7.7. Дапаўненне задачы недастаючымі дадзенымі: .Бабуля купіла 6м тканіны і пашыла 2 навалкі. Колькі метраў тканіны пайшло на кожную навалку? (Аднолькавы) ыбери номера правильных ответов В начальных классах геометрический материал изучается : 1) на пропедевтическом уровне; 2)на эмпирическом уровне; 3) на дедуктивном уровне; 4) на индуктивном уровне

У пачатковым курсе матэматыкі вучні знаёмяцца з велічынямі: даўжынёй, плошчай, масай, ёмкасцю, коштам, часам і інш. Паслядоўнасць вывучэння іх наступная:

1.Параўнанне прадметаў,іх малюнкаў,геаметрычных фігур па велічыні на аснове вокамеру, мускульнага адчування.

2. Параўнананне прадметаў, іх малюнкаў і фігур па велічыні шляхам накладання, на шалевых вагах і г.д.

3. Параўнанне геаметрычных фігур па велічыні на аснове ўвядзення адвольнай меркі, паяўлення ў выніку вымярэння цэлых неадмоўных лікаў і параўнання гэтых лікаў як мер велічынь. Змяненне вынікаў вымярэння ў выглядзе лікаў у залежнасці ад велічыні меркі.

Заданне, якое мае ўмову і патрабаванне, што патрэбна зрабіць, называюць задачай. Прыклады (Пр.):1) Вылічыць 9-2. 2) Рашыць няроўнасць 2+Х<9. 3) Пабудаваць квадрат, перыметр якога роўны 16 см.

Найбольш характэрны для матэматыкі тэкставыя або сюжэтныя задачы: "На адну талерку паклалі 20 вішань, што ў 2 разы больш,чым на другую (умова задачы). Колькі ўсяго вішань паклалі на талеркі ? (пытанне задачы)".

З тэкста задачы звычайна выдзяляюць:

ПРАДМЕТНУЮ ВОБЛАСЦЬ: дзве талеркі з вішнямі. ВЕЛІЧЫНІ-колькасць.

ЗНАЧЭННН1 ВЕЛІЧЫНІ:вядо-мыя-20вішань, невядомыя - 10в., шукаемае-30в. АДНОСІНЫ: у 2 разы больш.ЗАЛЕЖНАСЦІ: усяго.

РАШЭННЕ: (20:2)+20=30 (в.). АДКАЗ: паклалі 30 вішань.

Патрэбна адрозніваць паняцце "рашэнне задачы" як:

1) вынік (адказ-30в.); 2) спосаб рашэння задачы (а:2+а); 2) працэс пошуку спосабу; 3) план знаходжання адказу.

Рашэнне задачы можна зрабіць рознымі спосабамі: 1.ПРАКТЫЧНЫМ-з дапамогай канкрэтных прадметаў.

2.АРЫФМЕТЫЧНЫМ - рашэннем задачы па дзеяннях: 20:2=10(в.);10+20=30(в.) або састаўленнем выразу: 20:2+10.

3.АЛГЕБРАІЧНЫМ- з дапамогай ураўнення: х-20:2=20. 4. ГЕАМЕТРЫЧНЫМ -з дапамогай чарцяжа.

У пачатковых класах рашаюць задачы: 1) у прамой і ва ўскоснай форме; 2) з поўнымі, недастаючымі або з лішнімі дадзенымі ; 3) прамыя і адваротныя ім. Праверка рашэння задачы праводзіцца: 1) прыкідкай выніку; 2) рашэннем задачы другім спосабам; 3) рашэннем адваротнай задачы; 4) адпаведнасцю адказу ўмове задачы. Задачы бываюць: простыя на адно дзеянне, на два і больш дзеянняў - састаўныя з прыведзенымі або непрыведзенымі дадзенымі.

План

1,Далікавы перыяд навучання. 2. Дзесятак.

3. Дваццаць.

4. Сотня.

5,Тысяча.

6. Мнагазначныя лікі

Літаратура Асноўная 1 ГЛ. 4 2 ГЛ.1

Дадатковая 3 ГЛ. 2

Ключавыя словы; канцэнтры, класы і разрады, абак, памясцовы прынцып, алгарытмы, ўласцівасці арыфметычных дзеянняў

У гэты перыяд настаўнік павінен выявіць, адкарэтыраваць і паглыбіць ў вучняў уменні:

- упарадкоўваць мноствы прадметаў па форме, велічыні і колеру,класіфікаваць іх;

- параўноўваць мноствы прадметаў на аснове біекцыйнай адпаведнасці, ураўнівацьлічыць прадметы ў прамым і адваротным парадку, пачынаючы з любога ліку, валодаць правіламі лічэння, каб адказаць на пытанні: «Колькі?», «Які па ліку?»;

• называць суседзяў ліку, параўноўваць лікі;

• паказваць і называць лічбы і суадносіць іх з адпаведнай колькасцю прадметаў;

• паказваць і называць матэматычныя сімвалы («+», « -». «=», « > », « < »);

- рашаць простыя задачы на складанне і адніманне;

• паказваць і называць прасцейшыя геаметрычныя фігуры і іх элементы;

• валодаць прасторавымі ўяўленнямі тыпу «вышэй-н1жэй», «злева-справа», «зверху-знізу» і інш.;

• валодаць часовымі ўяўленнямі тыпу «сёння-заўтра-паслязаўтра-пазаўчора» і і.

-Паказ на канкрэтных мноствах утварэння новага ліку (а +1, а –1);

-назва ліку і паказ яго абазначэння лічбай;

- параўнанне ліку з папярэднімі лікамі з выкарыстаннем лікавага праменю і без яго;

- вызначэнне месца ліку ў радзе лікаў;

- паказ складу ліку рознымі спосабамі;

- навучанне пісьму лічбы, якая абазначае лік:

паказ узору напісання лічбы;

выдзяленне элементаў лічбы;

паказ паслядоўнасці пісьма;

пісьмо лічбы па ўзору і без яго. Асаблівасці знаёмстага вучняў з адназначнымі лікамі:

- лікі вывучаюцца адрэзкамі натуральнага раду лікаў ад кожнага да вывучаемага ліку;

-лік прадстаўляецца, як колькасць элементаў мноства (колькі?) і як член паслядоўнасці гэтых элементаў мноства ( які па ліку?);

- вывучаеца састаў ліку са складаемых;

- лік «0» вывучаецца пазней (пасля ліку 5).

тры 3

л ік назва ліку лічба

Этап	Выпадкі складання і аднімання	Прыёмы	Тэарэтычныя асновы
1.	а+1; а – 1	Прылічванне і адлічванне 1	Нумарацыя і ўтварэнне лікаў
2.	а+2; а+3; а+4 а-2; а-3; а-4	Прыбаўленне і адніманне ліку па частках	Сэнс дзеянняў складання і аднімання
3.	+ 5; 6; 7; 8; 9	Выкарыстанне перамяшчальнай ўласцівасці складання	Перамяшчальная уласцівасць складання
4.	- 5; 6; 7; 8; 9	Выкарыстанне сувязі дзеянняў складання і аднімання	Залежнасць паміж кампанентамі і вынікамі дзеянняў

Існуюць розныя падыходы да абгрунтаван-ня лікаў: тэарэтыка-мноствены, у якім натуральны лік прадстаўляе клас роўна-магутных мностваў; аксіяматычны, дзе вельмі добра паказаны прынцыпы ўтварэння натуральнага раду лікаў; велічыні, у якім лік вызначаецца як мера велі-чынь.Кожны натуральны лік можна прадставіцьяк суму лікаў, кратных ступеням дзесяці: 10ⁿ, 10^n-1, … 10¹ (разрадных лікаў). Пры гэтым множнікамі іх выступаюць толькі лікі 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.

103	102	101	100
1000	100	10	1
	5	3	9

Таму лік 539 прадстаўляецца так: 539=5 10²+3 10¹+9 10
Цана месца кожнай лічбы злева заўсёды ў 10 разоў меншая, чым справа. Кожныя тры паслядоўныя разрады ўтвараюць класы: 1-ы клас – клас адзінак (адз., дзес., сот); 2-і клас - клас тысяч (адз. тыс., дзес. тыс., сотні тыс.) і г.д. Гэта тлумачыць назву дзесятковай пазіцыйнай сістэмы лічэння. Чытаюцца і запісваюцца лікі па класах і разрадах.

Нагляднымі дапаможнікамі могуць быць:

палачкі, рассыпныя і звязаныя ў дзесятак кубікі і брусок з 10 кубікаў; лічыльнікі; абак.

Вывучаецца нумарацыя ў паслядоўнасці:

• Паўтарэнне матэрыялу аб адназначных ліках. Лік 10 – новая лічыльная адзінка.

• Атрыманне лікаў другога дзесятка пры-лічваннем да дзесятка некалькі адзінак.

тры – на – цаць

• Атрыманне ліку 20 з двух дзесяткаў.

• Дзясяткі	Адзінкі
  1	3

  Пісьмовая нумарацыя лікаў ад 11 да 20 з дапамогай абака і без яго.Знаёмства з дэцыметрам і пераўтварэннем мер даўжыні. Параўнанне з разраднымі адзінкамі: 1дз.3 адз.=13адз.; 35адз.=3дз.5адз. 1дм 3см=13см;

• 35 см=3дм 5см

• Знаёмства з прыёмамі складання і аднімання на аснове нумарацыі: 10+5=15; 15-5=10; 14+1=15; 15-1=14

СКЛАДАННЕ І АДНІМАННЕ ЛІКАЎ У МЕЖАХ 20

Вывучаецца ў наступнай паслядоўнасці:

1.Паўтарэнне прыёмаў складання і аднімання на аснове нумарацыі двухзначных лікаў.

2.Складанне і адніманне,калі да двухзна-чнага ліку прыбаўляецца адназначны лік або калі ад двухзначнага ліку аднімаецца адназначны лік:15+4=19; 17-5=12; 20-7=13.

3.Складанне, калі лік дапаўняецца да 10 і на аснове складу ліку вызначаецца і дадаецца да 10 лік, які застаўся.

2

9 + 3 = 12

9

2

3

+ = 10 + = 12 1 2

1

9 + 3 = (9+1) + 2 =12

4.Адніманне ад двухзначнага адназначнага ліку, калі памяншаемае прадстаўляецца ў выглядзе сумы двух складаемых, адно з якіх роўна аднімаемаму:15 – 8 =7; 15 – 8 = (8 +7) – 8 = 7

5 .Адніманне ад двухзначнага ліку адназначнага калі аднімаемае прадстаўляем у выглядзе сумы двух лікаў, адніманне аднаго з якіх дае 10: 15 - 8 = 7

15-8=15-(5+3)=7.

Наглядныя дапаможнікі: абакі, лічыльнікі.

Тэма вывучаецца ў паслядоўнасці:

1.Паўтарэнне нумарацыі лікаў у межах 20.

2.Прамое і адваротнае лічэнне дзес. да100 са звяртаннем увагі на назвы лікаў 40,90.

3.Увядзенне паняцця разрадныя лікі: 23 = 20+3 Дзес. Адз. 2 дзес. 3 адз. 2-і разрад-- 2 3----1-ы разрад

4.Запіс лікаў з апорай на абак і без яго.

5.Вывучэнне разраднага складу лікаў:

45= 40+5 або 4 дзес. і 5 адз.

6. Вывучэнне мер даўжыні : дм і см. Параўнанне: 65=6 дзес. 5адз. 65см=6дм 5см

7.Параўнанне лікаў з выкарыстаннем пра-меню без яго!---!---!---!---!---!---!---!---!---!---!

49< 50< 51 98< 99< 100

8.Практыкаванні на памясцовае значэнне лічбаў: уставіць лік 67, 68,....,70; запісаць адрэзак лікаў ад 87 да 90; параў-наць лікі 59 і 61.

9.Практыкаванні на параўнанне лікаў з пропускмі: 3*… 4*; ;3 дм 8 см... 5дм *см.

10.Выкананне складання і аднімання віду:

20+30; 90-80; 30 +2; 36 -6; 67 -1; 100-2.

Вывучаецца па плану на аснове ўласці- васцей П1_1,2: а (в+с)=а в с=а с в-пры-баўлення (аднімання) сумы да (ад) ліку;

П11_1.2 : (а+в) с=а с + в=а+в с -пры-баўленне (адніманне) ліку да (ад) сумы.

1.Складанне 2-зн. і 1-зн. лікаў тыпу: 57+3=

=(50+7)+3=50+(7+3)=50+10=60 (П11₁).

2.Адніманне ад круглых адназначн. лікаў:

40-8=(30+10)-8=30+(10-8)=30+2=32 (П1₂).

3.Складанне 2-зн. і 1-зн. лікаў з пераходам:

26+7=(23+3)+7=23+(3+7)=23+10=33 (П11₁).

4.Адніманне 1-зн. ліку ад 2-зн. з перах. праз разр.:35-7=35-(5+2)=(35-5)-2=30-2=28 (П1₂).

5.Складанне круглых з някругл. 2-зн. лікамі:

80+13=80+(10+3)=(80+10)+3=90+3=93 (П1₁).

6.Прыбаўленне (аднім.) круглых да (з) някруглых двухзначных лікаў:

34-20=(30+4)-20=(30-20)+4=14 (П11₂).

7.Складанне (адніманне) двухзначзых лікаў без пераходу праз разрад:

47-34=(40-30)+(7-4)=10+3=13(П1,П11).

8. Складанне 2-зн. лікаў з пер. праз разрад : 34+27=(30+4)+(20+7)=(30+20)+(4+7)=50+11

9.Адніманне ад круглых 2-зн. лікаў:80-24= =(70+10)-(20+4)=(70-20)+(10-4)=50+6=56.

10. Парадак выканання дзеянняў без дужак.

Выконваецца на аснове правіл прыбаўлення сумы да сумы і аднімання сумы ад сумы.

1. Складанне без пераходу праз разрад. 2.Складанне з пераходам праз разрад па алгарытму.

2.1.Падпісваем лікі, пачынаючы з адзінак. 2.2.Складваем спачатку адзінкі, а затым дзесяткі.

2. 3.Чытаем адказ.

3. Складанне з пераходам праз разрад. 4. Адніманне без пераходу праз разрад: 1.Адз. падпісв. пад адз.,дзес. пад дзес. 76 2.Аднімаю спачатку адз.,затым дзес. 32 3.Чытаю адказ. 44 5. Адніманне лікаў тыпу 80-25 6. Адніманне з пераходам праз разрад.

7.Праверка складання адніманнем, аднімання складаннем:25+32=57;57-25=32

выконваецца па плану:

1.Увядзенне множання як сумы аднолькавых складаемых 2+2+2+2=8 2•4 = 8.

2.Знаёмства з кампанентамі множання:

2•4 =8: 2 - 1-ы множнік, 4 - 2-і множнік,

8-здабытак.

3.Знаёмства з перамяшчальнай уласцівасцю множання:

х х х х х х 3 • 2 = 6 . 0 0 0 0 0 0 2 • 3 = 6.

4. Складанне табліцы множання на 2: оо оо 2+2=4 2• 2=4 5• 2=10 8• 2=16 ооо ооо 3+3=6 3• 2=6 6• 2=12 9• 2=18. оооо оооо 4+4=8 4• 2=8 7• 2=14

5.Складанне табліцы множання 2-ух: 2• 2=4 2• 2=4 4• 2=8 2• 4=8 6• 2=12 2• 6=12

3• 2=6 2•3=6 5•2=10 2•5=10 7• 2=14 2*7=14 6.Увядзенне дзялення як дзеяння, адваротнага множанню (дзяленне на роўныя часткі і па зместу):

Задачы: 1) Узялі 3 зялёныя і 3 чырвоныя перцы. Колькі ўсяго перцаў узялі? 3•2=6(п.). 2) Узялі 6 перцаў і падзялілі пароўну. Колькі перцаў у кожнага? 6:2=3 (п.)-дзял.на роўныя часткі.

3) 6 перцаў расклалі на талеркі па 3 на кожную.Колькі трэба талерак? 6:3=2(т.)-дзяленне па зместу.

7.Знаёмства з кампанентамі дзялення: 6:3=2 6-дзялімае, 3-дзельнік, 2-дзель, 6:3-дзель лікаў.

8.Складанне табліц дзял. на 2 і з дзеллю 2:

2• 2=4 4:2=2 4:2=2 2• 5=10 10:2=5 10:5=2

2• 3=6 6:2=3 6:3=2 2• 6=12 12:2=6 12:6=2

2• 4=8 8:2=4 8:4=2 2• 7=14 14 :2=7 14:7=2 ……………………………….. … 9.Цотныя лікі і асобыя выпадкі множ. і дзял.: а•1=а; а:1=а; а•0=0; 0•а=0; а:0-нельга. 10.Складанне табліц множання і дзялення на 3,4,5,6,7,8,9 з выкар. перамяшчальнай уласцівасці множання і сувязі мн. з дзял.: 2•2=4;3• 3=9; 4•4=16;5•5=25;6•6=36;7•7=49

2•3=6;3•4=12;4•5=20;5•6=30;6•7=42;7•8=56

....... .......... ....... .......... ............. .........

2•9=18;3•9=27;4•9=36;5•9=45;6•9=54;7•9=63Лік на сябе і на 9 8• 8=64 8• 9 =72;9• 9 =81

Выконваецца ў паслядоўнасці: 1. Множанне і дзяленне круглых лікаў: 20•3=60 2дз.•3=6дз. 80:40=2 8дз.:4дз.=2. 2. Вывад правіла множання сумы на лік: хххх ооо ( 4+3) • 2 = 14 хххх ооо ( 4+3) • 2= 4• 2 + 3• 2= 8 +6 = 14 3. Множанне тыпу : 34• 2=(30+4)•2=30• 2 +4• 2= 60+8 = 68. 4. Множанне тыпу: 2• 34=34• 2 =68. 5. Вывад правіла дзялення сумы на лік:

хххх оо (4 + 2) :2= 6 :2=3 хххх оо (4 + 2) :2= 4:2 + 2:2=2+1=3.

6. Выпадак дзялення, калі лік разбіваецца на суму разрадных складаемых: . 86:2=(80+6):2= 80:2+6:2= 40+3=43.

7. Выпадак дзялення, калі лік разбіваецца на суму зручных складаемых: 96:2= (80+16):2=80:2+16:2=40+8=48.

8. Дзяленне з астаткам на аснове табліц дзялення: 25:4=6 (аст.1) 9. Дзяленне падборам: 75:25=3. Усе выпадкі табл. і нетабл. дзеян. ляжаць у межах 100 і скар. у 2 р. па перамяшч. уласцівасц.

Агульны план і парадак вывучэння тэмы:

• увядзенне новых лічыльных адзінак (адзінкі тыс.., дзесяткі тыс.,сотні тыс.) і іх назваў;

• увядзенне паняццяў клас адзінак, клас тысяч;

• чытанне і запіс адзінак другога класу;

• чытанне і запіс адзінак першага і другога класу.